Trường Toán Online MATHX
Lớp 4 là một trong những năm học quan trọng của tiểu học. Đây là năm mà môn toán có kiến thức khó nhất khi bước vào giai đoạn mới của cấp hai. Chính vì vậy, việc bổ sung kiến thức cho môn toán và rất cần thiết. Học toán tư duy lớp 4 sẽ giúp cho trẻ có nên tảng học tập tốt hơn. Nhằm giúp các em tiếp cận gần hơn với Toán tư duy, đội ngũ MATHX biên soạn các bài toán tư duy về chủ đề Các dạng toán đặc biệt - Toán tư duy lớp 4 gồm các dạng toán trung bình cộng, tính tuổi, tư duy, toán dãy số và quy luật kèm bài tập vận dụng online có đáp án. Mời ba mẹ và các con cùng tham khảo!
Phụ huynh và các con tham khảo thêm một số nội dung toán tư duy lớp 4 kèm bài tập tại MATHX dưới đây nhé:
- Dạng 1: Tìm trung bình cộng
Phương pháp giải
Bước 1: Xác định số các số hạng có trong bài toán.
Bước 2: Tính tổng các số hạng vừa tìm được.
Bước 3: Trung bình cộng = “Tổng của các số đó” chia cho “số các số hạng”.
Ví dụ: Trường tiểu học Lương Thế Vinh có 3 lớp tham gia trồng cây. Lớp 4A trồng được 17 cây, lớp 4B trồng được 13 cây, lớp 4C trồng được 15 cây. Hỏi trung bình mỗi lớp trồng được bao nhiêu cây?
Bài giải
Có 3 lớp tham gia trồng cây số các số hạng là 3
Tổng số cây cả ba lớp trồng là:
17 + 13 + 15 = 45 (cây)
Trung bình mỗi lớp trồng được số cây là:
45 : 3 = 15 (cây)
Đáp số: 15 cây
Trung bình cộng của dãy cách đều bằng:
- Số ở chính giữa (nếu dãy có các số hạng là số lẻ).
- Trung bình cộng 2 số ở giữa (nếu dãy có các số hạng là số chẵn).
- Trung bình cộng = (số đầu + số cuối) : 2
Ví dụ: Tìm trung bình cộng của các số sau:
1, 3, 5, 7, 9
Bài giải
Trung bình cộng của các số là:
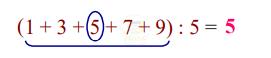
Đáp số: 5
- Dạng 2: Tìm giá trị của trung bình cộng.
Ví dụ: Tìm 5 số lẻ liên tiếp biết trung bình cộng của chúng bằng 2011
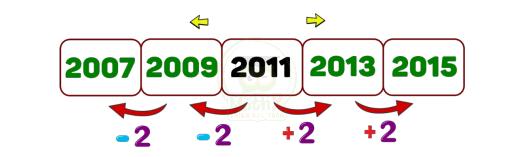
Trung bình cộng của dãy cách đều bằng số ở chính giữa (nếu dãy có các số hạng là số lẻ)
- Dạng 3: Nhiều hơn, ít hơn trung bình cộng.
Ví dụ:
Xe thứ nhất chứa được 45 tấn hàng, xe thứ hai chứa được 53 tấn hàng, xe thứ ba chứa được số hàng nhiều hơn trung bình cộng số tấn hàng của hai xe đầu là 6 tấn. Hỏi xe thứ ba chở được bao nhiêu tấn hàng.
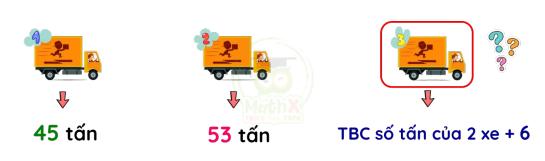
Bài giải
Trung bình cộng số tấn hàng hai xe đầu chở được là:
(45 + 53) : 2 = 49 (tấn)
Số tấn hàng xe thứ ba chở được là:
49 + 6 = 55 (tấn)
Đáp số: 55 tấn
- Dạng 1: Điền thêm số hạng vào dãy số.
Các quy luật thường gặp của dãy số:
+ Số hạng đứng sau bằng số hạng đứng trước nhân với số thứ tự của nó.
+ Mỗi số hạng (kể từ số hạng thứ 2) trở đi đều bằng a lần số liền trước nó.
+ Mỗi số hạng (kể từ số hạng thứ 2) bằng số hạng đứng trước nó cộng (hoặc trừ) với một số tự nhiên n.
+ Mỗi số hạng (kể từ số hạng thứ 3) bằng tổng hai số hạng đứng liền trước nó.
+ Mỗi số hạng (kể từ số hạng thứ 4) bằng tổng của số hạng đứng trước nó cộng với số tự nhiên b rồi cộng với số thứ tự của số hạng ấy.
Ví dụ: Tìm giá trị của các con vật trong dãy số sau.
1; 2; 3; 5; 8; ... ; ...; ...
Bài giải
Ta thấy: 1 + 2 = 3 ; 2 + 3 = 5 ; 3 + 5 = 8
Kể từ số hạng thứ 3 trở đi mỗi số hạng bằng tổng của hai số hạng đứng liền trước nó.
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
Vậy: 1; 2; 3; 5; 8; 13; 21; 34
- Dạng 2: Tìm số số hạng của dãy số cách đều:
+ Công thức 1: Số các số hạng của dãy = số khoảng cách + 1.
Ví dụ: Viết các số lẻ liên tiếp từ 211. Số cuối cùng là 971. Hỏi viết được bao nhiêu số?
Bài giải
Số cuối cách số đầu số đơn vị là:
971 – 211 = 760 (đơn vị)
760 đơn vị có số khoảng cách là:
760 : 2 = 380 (khoảng cách)
Số số hạng của dãy số trên là:
380 + 1 = 381 (số)
+ Công thức 2: Số các số hạng của dãy = (Số hạng lớn nhất – Số hạng nhỏ nhất ) : khoảng cách + 1.
Ví dụ: Tìm số số hạng của dãy số sau.
1, 4, 7, 10, 13, 16, 19, …, 94, 97, 100
Bài giải
Xác định
- Số đầu: 1
- Số cuối: 100
- Khoảng cách: 3
Số số hạng của dãy số là:
(100 – 1) : 3 + 1 = 34 (số hạng)
Đáp số: 34 số hạng
Dạng 3: Tìm tổng dãy số cách đều.
Phương pháp giải
Ví dụ: Tính tổng các số tự nhiên chẵn từ 0 đến 100.
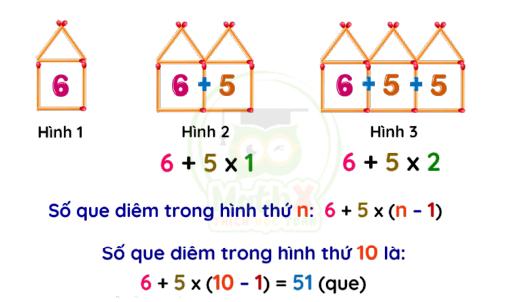
Ví dụ: Hỏi có bao nhiêu que diêm trong hình thứ 10.
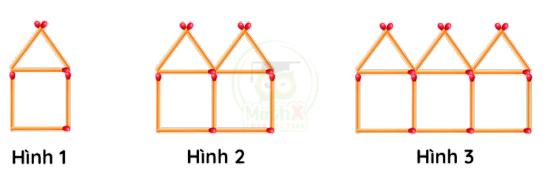
Bài giải
Dạng 1: Tìm số chữ số của dãy khi biết số số hạng
Phương pháp giải
Tính số chữ số từ trang 1 – 9; 10 – 99; 101 – 999;…
Sau đó cộng tất cả lại ta sẽ được đáp số.
Áp dụng các công thức tính:
Số số hạng = (Số cuối – Số đầu) : Khoảng cách giữa hai số + 1
Ví dụ: Để đánh số trang của một quyển sách dày 238 trang cần dùng bao nhiêu chữ số?
Bài giải
Từ 1 đến 9 có:
(9 – 1) : 1 + 1 = 9 (số có một chữ số)
Từ 10 đến 99 có:
(99 – 10) : 1 + 1 = 90 (số có hai chữ số)
Từ 100 đến 238 có: (238 – 100) : 1 + 1 = 139 (số có ba chữ số)
Vậy 238 trang cần dùng số chữ số là:
1 x 9 + 2 x 90 + 3 x 139 = 606 (số chữ số)
Đáp số: 606 số chữ số
- Dạng 2: Tìm số số hạng khi biết chữ số.
Ví dụ: Để đánh số trang 1 quyển sách người ta dùng hết 435 chữ số. Hỏi quyển sách đó có bao nhiêu trang?
Số trang sách có 1 chữ số là 9 số nên: 1 x 9 = 9 (chữ số)
Số trang sách có 2 chữ số là 90 số nên: 2 x 90 = 180 (chữ số)
Số chữ số để đánh số trang sách có 3 chữ số là: 435 – 9 – 180 = 246 (chữ số)
246 chữ số thì đánh được số trang có 3 chữ số là: 246 : 3 = 82 (trang)
Quyển sách đó có số trang là: 9 + 90 + 82 = 181 (trang)
Đáp số: 181 trang
Câu 6: Hỏi có bao nhiêu que diêm trong hình thứ 99?
Câu 8: Cha hơn con 32 tuổi. Sau 4 năm nữa thì tuổi cha gấp ba lần tuổi con. Hỏi tuổi cha và tuổi con hiện nay là bao nhiêu tuổi?
Trên đây là những nội dung lý thuyết và bài tập vận dụng về Các dạng toán đặc biệt - Toán tư duy lớp 4. Hi vọng những chia sẻ vừa rồi của MATHX sẽ giúp các em có thêm hành trang vững bước trong quá trình học tập của bản thân. Chúc các em học tập hiệu quả!!
Ngoài ra các em có thể tham khảo thêm các khóa học Toán Lớp 4 gồm các khóa học ôn tập hè, luyện toán tiếng anh, toán tư duy, toán nâng cao, luyện đề học sinh giỏi… trong link sau: Các khóa học toán lớp 4 tại MATHX
Lưu ý: Các em cần Tạo Tài Khoản và Đăng Nhập để có thể xem được những nội dung này