Bài toán bất đẳng thức hay dành cho học sinh thi chuyên toán

Có bạn học sinh hỏi thầy Hiếu bài toán khó về BĐT như sau, tiện thầy Hiếu post lên đây để các bạn học sinh có mục tiêu thi HSG lớp 9, thi chuyên toán tham khảo.

Đề bài và lời giải.

Bài 4. Cho ba số thực dương \( a, b, c \) thỏa mãn \( ab + bc + ca = 1 \). Tìm giá trị lớn nhất của biểu thức

\( P = \dfrac{2a}{\sqrt{1 + a^2}} + \dfrac{b}{\sqrt{1 + b^2}} + \dfrac{c}{\sqrt{1 + c^2}} \)

Ta có:

• \( 1 + a^2 = ab + bc + ca + a^2 = (a + b)(a + c) \)
• \( 1 + b^2 = ab + bc + ca + b^2 = (b + a)(b + c) \)
• \( 1 + c^2 = ab + bc + ca + c^2 = (c + a)(c + b) \)

Thay vào:

\( P = \dfrac{2a}{\sqrt{(a + b)(a + c)}} + \dfrac{b}{\sqrt{(b + a)(b + c)}} + \dfrac{c}{\sqrt{(c + a)(c + b)}} \)

Sử dụng bất đẳng thức AM-GM và kỹ thuật tách đôi:

\[ \begin{aligned} P &= \sqrt{\dfrac{2a}{a + b}} \cdot \sqrt{\dfrac{2a}{a + c}} + \sqrt{\dfrac{2b}{b + a}} \cdot \sqrt{\dfrac{b}{2(b + c)}} + \sqrt{\dfrac{2c}{c + a}} \cdot \sqrt{\dfrac{c}{2(c + b)}} \\ &\leq \frac{1}{2} \left( \dfrac{2a}{a + b} + \dfrac{2a}{a + c} \right) + \frac{1}{2} \left( \dfrac{2b}{b + a} + \dfrac{b}{2(b + c)} \right) + \frac{1}{2} \left( \dfrac{2c}{c + a} + \dfrac{c}{2(c + b)} \right) \end{aligned} \]

Sau khi biến đổi, rút gọn:

\( P \leq \dfrac{1}{2} \cdot 2 + \dfrac{1}{2} \cdot 2 + \dfrac{1}{4} = \dfrac{9}{4} \)

Dấu “=” xảy ra khi: \( a = \dfrac{7}{\sqrt{15}} \), \( b = c = \dfrac{1}{\sqrt{15}} \)

Sau khi giải, chúng ta hãy tổng quát bài toán như sau:

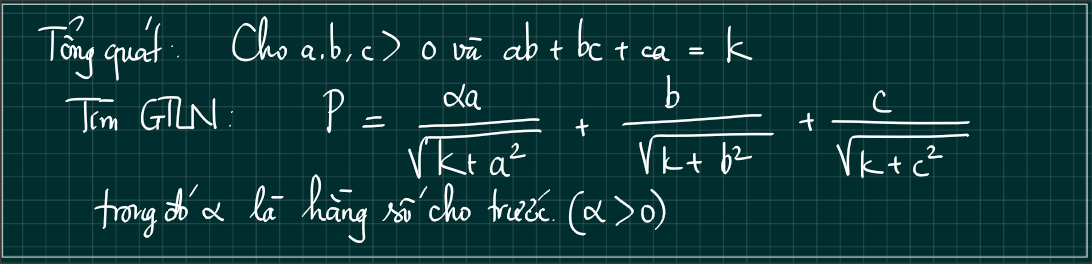
Một hướng mở rộng để các bạn yêu toán tìm tòi nhé.

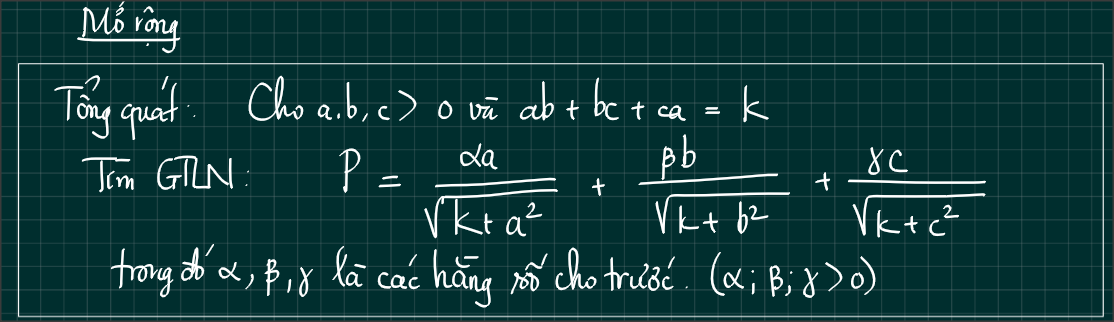
Các em tham khảo thêm khoá học Toán lớp 9 tại đây:

Học toán lớp 9 MATHX

GIỚI THIỆU LỚP HỌC ONLINE CÙNG GIÁO VIÊN GIỎI