
MATHX.VN biên soạn bộ đề kiểm tra giữa kì 2 Toán 7 năm 2023 kèm lời giải chi tiết giúp các em học sinh nhanh chóng làm quen với cấu trúc đề thi, ôn tập để đạt được kết quả cao trong kì thi giữa học kì sắp tới. Mời các em cùng tham khảo dưới đây!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Bài 1. Tìm x biết:
a) \(-0,1:x=-0,2:0,06\)
b) \({\dfrac{2-x}{4}}={\dfrac{3x-1}{3}}\)
Lời giải:
a) \(-0,1:x=-0,2:0,06\)
\({\dfrac{-0,1}{x}}={\dfrac{-0,2}{0,06}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-1}{5}}:{\dfrac{3}{50}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-1}{5}}.{\dfrac{3}{50}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-10}{3}}\)
Áp dụng tính chất tỉ lệ thức ta có:
-0,1 . 3 = -10x
-0,3 = -10x
\(x=-0,3:(-10)\)
\(x={\dfrac{-3}{10}}.\left({\dfrac{1}{-10}}\right)\)
\(x = \dfrac{3}{100}\)
Vậy \(x = \dfrac{3}{100}\)
b) \({\dfrac{2-x}{4}}={\dfrac{3x-1}{3}}\)
\(3\left(2-x\right)=4\left(3x-1\right)\)
\(-3x-12x=-4-6\)
-15x = -10
\(x = \dfrac{2}{3}\)
Vậy \(x = \dfrac{2}{3}\)
Bài 2. Ba đơn vị kinh doanh A, B và C góp vốn theo tỉ lệ 2:3:7 sau một năm thu được tổng cộng 960 triệu đồng tiền lãi. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi biết tiền lãi được chia tỉ lệ thuận với số vốn đã góp.
Lời giải:
Gọi số tiền lãi của ba đơn vị kinh doanh A, B và C lần lượt là x,y,z (triệu đồng) (điều kiện: x,y,z > 0)
Theo bài ra, ta có: \(\left\{ \begin{array}{} \dfrac {x} {2}=\dfrac {y} {3}=\dfrac{z}{7} \\ x + y + z =960 \\ \end{array} \right.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\({\dfrac{x}{2}}={\dfrac{y}{3}}={\dfrac{z}{7}}={\dfrac{x+y+z}{2+3+7}}={\dfrac{960}{12}}=80\)
Khi đó, \({\dfrac{x}{2}}\,=\,80\,\Rightarrow\,x\,=160\) (tmđk)
\({\dfrac{y}{3}}\,=\,80\,\Rightarrow\,y\,=240\) (tmđk)
\({\dfrac{z}{7}}\,=\,80\,\Rightarrow\,y\,=560\) (tmđk)
Vậy số tiền lãi của ba đơn vị kinh doanh là: Đơn vị A: 160 triệu đồng, đơn vị B: 240 triệu đồng, đơn vị C: 560 triệu đồng.
Bài 3. Cho các đa thức:
\(F\left(x\right)=5x^{2}-1+3x+x^{2}-5x^{3}\) và \(G\left(x\right)=2-3x^{3}+6x^{2}+5x-2x^{3}-x.\)
a) Thu gọn và sắp xếp hai đa thức F(x) và G(x) theo lũy thừa giảm dần của biến.
b) Tính M(x) = F(x) - G(x); Tìm nghiệm của đa thức M(x)
c) Tìm đa thức N(x) Biết \(N\left(x\right)+F\left(x\right)=-G\left(x\right)\)
Lời giải:
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
Thu gọn F(x):
\(F\left(x\right)=5x^{2}-1+3x+x^{2}-5x^{3}\)
\(F\left(x\right)=-5x^{3}+\left(5x^{2}+x^{2}\right)+3x-1\)
\(F\left(x\right)=-5x^{3}+6x^{2}+3x-1\)
Thu gọn G(x):
\(G\left(x\right)=2-3x^{3}+6x^{2}+5x-2x^{3}-x.\)
\(G\left(x\right)=\left(-3x^{3}-2x^{3}\right)+6x^{2}+\left(5x-x\right)+2\)
\(G\left(x\right)=-5x^{3}+6x^{2}+4x+2\)
b) Tính M(x)
M(x) = F(x) - G(x)
\(M\left(x\right)=\left(-5x^{3}+6x^{2}+3x-1\right)-\left(-5x^{3}+6x^{2}+4x+2\right)\)
\(M\left(x\right)=-5x^{3}+6x^{2}+3x-1+5x^{3}-6x^{2}-4x-2\)
\(M\left(x\right)=\left(-5x^{3}+5x^{3}\right)+\left(6x^{2}-6x^{2}\right)+\left(3x-4x\right) + (-1-2)\)
M(x) = -x - 3
Tìm nghiệm của đa thức M(x):
Ta có: \(M\left(x\right)=-x-3=0\Leftrightarrow x=-3\)
Vậy x = -3 là nghiệm của đa thức M(x).
c) Ta có: \(N\left(x\right)+F\left(x\right)=-G\left(x\right)\)
\(\Rightarrow N\left(x\right)=-F\left(x\right)-G\left(x\right)=-\left[F\left(x\right)+G\left(x\right)\right]\)
Trong đó:
\(F\left(x\right)=-5x^{3}+6x^{2}+3x-1\)
\(G\left(x\right)=-5x^{3}+6x^{2}+4x+2\)
=> F(x) + G(x)
\(=\left(-5x^{3}+6x^{2}+3x-1\right)+\left(-5x^{3}+6x^{2}+4x+2\right)\)
\(=-10x^{3}+12x^{2}+7x+1\)
\(\Rightarrow N\left(x\right)=-\left[F\left(x\right)+G\left(x\right)\right]\)
\(=-\left(-10x^{3}+12x^{2}+7x+1\right)\)
\(=10x^{3}-12x^{2}-7x-1\)
Vậy \(N\left(x\right)=10x^{3}-12x^{2}-7x-1.\)
Bài 4. Cho ΔABC cân tại A có AM là đường trung tuyến.
a) Chứng minh ΔAMB = ΔAMC
b) Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh BC là tia phân giác của \(\widehat{A B D}\)
c) Lấy điểm E trên đoạn thẳng MC sao cho EC = 2EM, gọi I là trung điểm DC.
Chứng minh: 2EI < AB + CE
Lời giải:
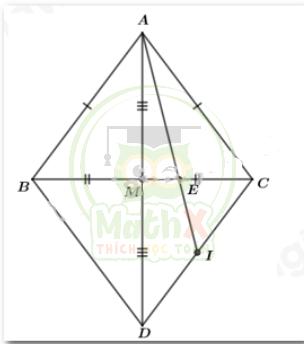
a) Vì ΔABC cân tại A ⇒ AB = AC
Vì AM là trung tuyến nên BM = MC
Vì ΔABC cân tại A có AM là trung tuyến nên AM cũng là đường cao
⇒ AM ⊥ BC
Xét ΔAMB và ΔAMC có:
AM chung
AB = AC (cmt)
BM = MC (cmt)
=> ΔAMB = ΔAMC (c.c.c) (đpcm)
b) Xét ΔBAM = ΔBDM có:
BM chung
AM = MD
=> ΔBAM = ΔBDM (c.g.c)
=> \(\widehat{A B M}\) = \(\widehat{DBM}\) (2 góc tương ứng)
=> BC là tia phân giác \(\widehat{A B D}\) (đpcm)
c) Xét ΔACD có CM là đường trung tuyến, điểm E thuộc CM thỏa mãn \({\dfrac{C E}{C M}}={\dfrac{2}{3}}\Rightarrow E\) là trọng tâm ΔACD
=> AE là đường trung tuyến của ΔACD
Lại có I là trung điểm DC ⇒ A, E, I thẳng hàng và AE = 2EI
Xét ΔAEC, áp dụng bất đẳng thức tam giác ta có:
AE < AC + EC
Mà \(A C=A B\Rightarrow2E I=A E\lt A B+E C\) (đpcm).
Bài 5. Cho tam giác ABC có trung tuyến AM. Chứng minh rằng AB + AC > 2AM
Lời giải:
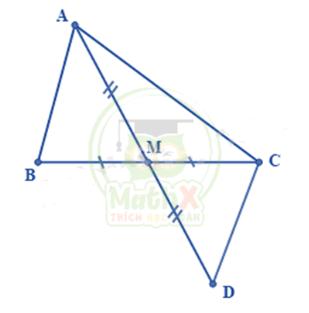
Do AM là trung tuyến của tam giác ABC nên ta có BM = CM.
Trên tia đối của tia AM lấy điểm D sao cho AM = DM.
Xét ΔAMB và ΔDMC có:
AM = DM
BM = CM
\(\widehat{AMB}\) = \(\widehat{DMC}\) (hai góc đối đỉnh)
Suy ra ΔAMB và ΔDMC (c.g.c) suy ra AB = CD (hai cạnh tương ứng)
Khi đó \(A B+A C=D C+A C\gt A D\) (bất đẳng thức tam giác)
Mà AM = DM nên AD = 2.AM
Do đó: AB + AC > 2AM
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 - đề 3. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.