HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN CHUYÊN THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2015 2016 - MATHX

 

Mathx.vn biên soạn gửi tới các em hướng dẫn giải đề thi tuyển sinh lớp 10 môn toán chuyên trường THPT Chuyên Hà Nội Amsterdam năm học 2015 2016. Các em học sinh tải đề về làm trước ra giấy sau đó so sánh kết quả và cách giải chi tiết trong bài viết này để đạt được hiệu quả ôn tập tốt nhất. Chúc các em học tốt và đạt kết quả cao trong kì thi THPT sắp tới!!

 

 

 

 

 

KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN

TRƯỜNG THPT CHUYÊN HÀ NỘI AMSTERDAM

ĐỀ THI TUYỂN SINH LỚP 10

(ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

Môn thi: Toán chuyên

Năm học: 2015 - 2016

Thời gian làm bài: 150 phút

(Dành cho học sinh thi chuyên Toán)

 

 

 

Bài 1 (2,0 điểm).

 

1) Giải phương trình:

$x-\sqrt{x-8}-3\sqrt{x}+1=0$

 

2) Giải hệ phương trình:

 

$\left\{ \begin{align} & {{x}^{2}}+{{y}^{2}}=5 \\ & {{x}^{3}}+2{{y}^{3}}=10x-10y \\ \end{align} \right.$

 

 

Giải

 

1) Giải phương trình:  $x-\sqrt{x-8}-3\sqrt{x}+1=0.$ (1)

ĐK: x ≥ 8

(1)   $\begin{align}   & \Leftrightarrow 2x-2\sqrt{x-8}-6\sqrt{x}+2=0 \\  & \Leftrightarrow (x-8-2\sqrt{x-8}+1)+(x-6\sqrt{x} \\  & \Leftrightarrow {{(\sqrt{x-8}-1)}^{2}}+{{(\sqrt{x}-3)}^{2}}=0 \\ \end{align}$    (2)

Ta có:

$\left\{ \begin{align}   & {{\left( \sqrt{x-8}-1 \right)}^{2}}\ge 0 \\  & {{\left( \sqrt{x}-3 \right)}^{2}}\ge 0 \\ \end{align} \right.\Rightarrow {{\left( \sqrt{x-8}-1 \right)}^{2}}+{{\left( \sqrt{x}-3 \right)}^{2}}\ge 0$

 

Do đó

$(2)\Leftrightarrow \left\{ \begin{align}   & \sqrt{x-8}-1=0 \\  & \sqrt{x}-3=0 \\ \end{align} \right.\Leftrightarrow x=9$  (thỏa mãn)

Vậy tập nghiệm của phương trình là {9}

 

2) Giải hệ phương trình

$\left\{ \begin{align}   & {{x}^{2}}+{{y}^{2}}=5 \\  & {{x}^{3}}+2{{y}^{3}}=10x-10y \\ \end{align} \right.$  (I)

 

 

(I)   $\Leftrightarrow \left\{ \begin{align}   & {{x}^{2}}+{{y}^{2}}=5 \\  & {{x}^{3}}+2{{y}^{3}}=2({{x}^{2}}+{{y}^{2}})(x-y) \ \ (*) \\ \end{align} \right.$ 

(*)   $\Leftrightarrow {{x}^{3}}+2{{y}^{3}}=2{{x}^{3}}-2{{x}^{2}}y+2x{{y}^{2}}-2{{y}^{3}} \\ \Leftrightarrow {{x}^{3}}-2{{x}^{2}}y+2x{{y}^{2}}-4{{y}^{3}}=0 \\ \Leftrightarrow (x-2y)({{x}^{2}}+2{{y}^{2}})=0 \\$  $\Leftrightarrow \left[ \begin{align}   & x=2y \\  & {{x}^{2}}+2{{y}^{2}}=0 \\ \end{align} \right.$

Ta có  ${{x}^{2}}+2{{y}^{2}}=0\Leftrightarrow x=y=0$  không là nghiệm của hệ.

Do đó
(I)  $\left\{ \begin{align}   & {{x}^{2}}+{{y}^{2}}=5 \\  & x=2y \\ \end{align} \right.$

  $\Leftrightarrow \left\{ \begin{align}   & 4{{y}^{2}}+{{y}^{2}}=5 \\  & x=2y \\ \end{align} \right.$

  $\Leftrightarrow \left\{ \begin{align}   & y=1 \\  & x=2 \\ \end{align} \right.$

hay $\left\{ \begin{align}   & y=-1 \\  & x=-2 \\ \end{align} \right.$

 

Vậy hệ có nghiệm (2;1) và (–2;–1)

 

 

 

Bài 2 (2,5 điểm)

 

1) Cho số nguyên dương n thỏa mãn n và 10 là hai số nguyên tố cùng nhau. Chứng minh

$({{n}^{4}}-1) \ \vdots \ 40$

 

2) Tìm tất cả các số nguyên tố p và các số nguyên dương x,y thỏa mãn

$\left\{ \begin{align}   & p-1=2x(x+2) \\  & {{p}^{2}}-1=2y(y+2) \\ \end{align} \right.$

 

3) Tìm tất cả các số nguyên dương n sao cho tồn tại các số nguyên dương x, y, z thoả mãn

${{x}^{3}}+{{y}^{3}}+{{z}^{3}}=n{{x}^{2}}{{y}^{2}}{{z}^{2}}$

 

 

Giải

 

1) Cho số nguyên dương n thỏa mãn n và 10 là hai số nguyên tố cùng nhau. Chứng minh

$({{n}^{4}}-1) \ \vdots \ 40$

Vì n và 10 là nguyên tố cùng nhau nên n không chia hết cho 2 và 5.

⇒ n chỉ có thể có dạng 10k ± 1 và 10k ± 3 với k ∈ ℕ.

Ta có:

${{n}^{4}}-1=({{n}^{2}}-1)({{n}^{2}}+1)=(n-1)(n+1)({{n}^{2}}+1)$

Do n lẻ nên $n – 1 \ ⋮ \ 2; n + 1 \ ⋮ \ 2$ và ${{n}^{2}} + 1 \ ⋮ \ 2 ⇒ {{n}^{4}} – 1 \ ⋮ \ 8$.   (1)

- Nếu n = 10k ± 1 ⇒ n² ≡ (±1)² ≡ 1 (mod 10) ⇒ n² – 1 ⋮ 10 ⇒ n⁴ – 1 ⋮ 5    (2)

Từ (1) và (2), chú ý (5;8) = 1

=> n⁴ – 1 ⋮ 40

- Nếu n = 10k ± 3 ⇒ n² ≡ (±3)2 = 9 (mod 10) ⇒ n² + 1 ⋮ 10 ⇒ n⁴ – 1 ⋮ 5    (3)

Từ (1) và (3) chú ý (5;8) = 1

=>  n⁴ – 1⋮ 40

Vậy trong mọi trường hợp ta có n⁴ – 1 ⋮ 40

 

2) Tìm tất cả các số nguyên tố p và các số nguyên dương x,y thỏa mãn

$\left\{ \begin{align}   & p-1=2x(x+2) \ \ (1) \\  & {{p}^{2}}-1=2y(y+2) \ \ (2) \\ \end{align} \right.$

 

Từ (1) ⇒ p – 1 là số chẵn ⇒ p là số nguyên tố lẻ.

Trừ từng vế của (2) cho (1) ta được
${{p}^{2}}-p=2{{y}^{2}}-2{{x}^{2}}+4y-4x\Leftrightarrow p(p-1)=2(y-x)(y+x+2) \ \ (*)$

⇒ 2(y – x)(y + x + 2) ⋮ p.

Mà (2;p) = 1 nên xảy ra 2 TH:

•  y – x ⋮ p ⇒ y – x = kp (k ∈ ℕ*)

Khi đó từ (*)

⇒ p – 1 = 2k(x + y + 2)

⇒ kp – k = 2k²(x + y + 2)

⇒ y – x – k = 2k²(x + y + 2)

(loại vì x + y + 2 > y – x – k > 0 ; 2k² > 1 ⇒ 2k²(x + y + 2) > y – x – k)

 

• y + x + 2 ⋮ p ⇒ x + y + 2 = kp (k ∈ ℕ*)

Từ (*)

⇒ p – 1 = 2k(y – x)

⇒ kp – k = 2k²(y – x)

⇒ x + y + 2 – k = 2k²(y – x)   (**)

Ta chứng minh k = 1. Thật vậy nếu k ≥ 2 thì từ (**)

⇒ x + y = 2k²(y – x) + k – 2 ≥ 8(y – x) (vì y – x > 0)

⇒ 9x ≥ 7y ⇒ 7y < 14x ⇒ y < 2x

Do đó từ (2)

⇒ (p – 1)(p + 1) = 2y(y + 2) < 4x( 2x + 2) < 4x(2x + 4) = 8x( x + 2) = 4(p – 1)

(vì 2x(x + 2) = p – 1 theo (1))

⇒ p + 1 < 4 ⇒ p < 3, mâu thuẫn với p là số nguyên tố lẻ.

Do đó k = 1, suy ra
$\left\{ \begin{align}   & x+y+2=p \\  & p-1=2(y-x) \\ \end{align} \right.$

$\Leftrightarrow \left\{ \begin{align}   & x+y+2=p \\  & x+y+1=2(y-x) \\ \end{align} \right.$

$\Leftrightarrow \left\{ \begin{align}   & x+y+2=p \\  & y=3x+1 \\ \end{align} \right.$

$\Leftrightarrow \left\{ \begin{align}   & y=3x+1 \\  & p-1=4x+2 \\ \end{align} \right.$

Thay p – 1 = 4x + 2 vào (1) ta có:
$4x+2=2x(x+2)\Leftrightarrow 2x+1={{x}^{2}}+2x\Leftrightarrow {{x}^{2}}=1\Rightarrow x=1$

⇒ y = 4, p = 7 (thỏa mãn)

Vậy x = 1, y = 4 và p = 7.

 

3) Tìm tất cả các số nguyên dương n sao cho tồn tại các số nguyên dương x, y, z thoả mãn

${{x}^{3}}+{{y}^{3}}+{{z}^{3}}=n{{x}^{2}}{{y}^{2}}{{z}^{2}}$   (1)

 

Giả sử n là số nguyên dương sao cho tồn tại các số nguyên dương x,y,z thỏa mãn (1)

Không mất tính tổng quát, giả sử x ≥ y ≥ z ≥ 1.

Từ (1)

$\Rightarrow 0<{{y}^{3}}+{{z}^{3}}={{x}^{2}}(n{{y}^{2}}{{z}^{2}}-1)\Rightarrow n{{y}^{2}}{{z}^{2}}-1>0\Rightarrow n{{y}^{2}}{{z}^{2}}-1\ge 1$

$\Rightarrow {{y}^{3}}+{{z}^{3}}={{x}^{2}}(n{{y}^{2}}{{z}^{2}}-1)\ge {{x}^{2}}(*)$

Vì x ≥ y ≥ z nên

$3{{x}^{3}}\ge {{x}^{3}}+{{y}^{3}}+{{z}^{3}}=n{{x}^{2}}{{y}^{2}}{{z}^{2}}\Rightarrow n{{y}^{2}}{{z}^{2}}\Rightarrow 9{{x}^{2}}\ge {{n}^{2}}{{y}^{4}}{{z}^{4}}$

Kết hợp với (*) ta có

$9\left( {{y}^{3}}+{{z}^{3}} \right)\ge 9{{x}^{2}}\ge {{n}^{2}}{{y}^{4}}{{z}^{4}}\Rightarrow 9\left( 1+\dfrac{{{z}^{3}}}{{{y}^{3}}} \right)\ge {{n}^{2}}y{{z}^{4}}$

Mà $y\ge z\Rightarrow \dfrac{{{z}^{3}}}{{{y}^{3}}}\le 1\Rightarrow {{n}^{2}}y{{z}^{4}}\le 9\left( 1+\dfrac{{{z}^{3}}}{{{y}^{3}}} \right)\le 18 \ \ (**)$

Ta có: (**)  $\Rightarrow {{z}^{4}}\le 18\Rightarrow \left[ \begin{align}   & z=1 \\  & z=2 \\ \end{align} \right.$

• Nếu z = 2 : (**) $\Rightarrow 16{{n}^{2}}y\le 18\Rightarrow n=y=1$ (loại vì y < z)
• Nếu z = 1 : (**) $\Rightarrow {{n}^{2}}y\le 18\Rightarrow {{n}^{2}}\le 18\Rightarrow n\le 4$

Ta chứng minh n ∉ {2;4}. Thật vậy,

• Nếu n = 4 thì từ n²y ≤ 18 ⇒ 16y ≤ 18 ⇒ y = 1. Từ (1) ⇒ x³ + 2 = 4x² ⇒ x²(4 – x) = 2 ⇒ x² là ước của 2 ⇒ x = 1 (không thỏa mãn)
• Nếu n = 2 thì từ n²y ≤ 18 suy ra 4y ≤ 18 ⇒ 1 ≤ y ≤ 4.

+ $y=1:(1)\Rightarrow {{x}^{3}}-2{{x}^{2}}+2=0\Rightarrow {{x}^{2}}(x-2)=-2<0\Rightarrow x<2\Rightarrow x=1 \ \ (L)$

+ $y=2:(1)\Rightarrow {{x}^{3}}-8{{x}^{2}}+9=0\Rightarrow 9={{x}^{2}}(8-x).$   Suy ra x2 là ước của 9. Mà x2 ≥ y2 = 4 nên x=3 (không thỏa mãn)

+ $y=3:(1)\Rightarrow {{x}^{3}}-18{{x}^{2}}+28=0\Rightarrow {{x}^{2}}(18-x)=28.$ Suy ra x² là ước của 28. Mà x² ≥ y² = 9 nên không tồn tại x thỏa mãn.

+ $y=4:(1)\Rightarrow {{x}^{3}}-32{{x}^{2}}+65=0\Rightarrow {{x}^{2}}$ là ước của 65 (loại vì 65 không có ước chính phương)

Vậy n ∉ {2;4}. Do đó n ∈ {1;3}

Thử lại với n = 1, tồn tại bộ (x;y;z) nguyên dương chẳng hạn (x;y;z) = (3;2;1) thỏa mãn (1)

với n = 3, tồn tại bộ (x;y;z) = (1;1;1) thỏa mãn (1).

Vậy tất cả các giá trị n thỏa mãn bài toán là n ∈ {1;3}

 

 

Bài 3 (1,5 điểm)

 

Cho ba số thực dương a, b, c thỏa mãn $(a + b)(b + c)(c + a) = 1$. Chứng minh $ab + ac + bc ≤ \dfrac{3}{4}$

 

 

Giải

 

Cho ba số thực dương a, b, c thỏa mãn $(a + b)(b + c)(c + a) = 1$   (1) . Chứng minh $ab + ac + bc ≤ \dfrac{3}{4}$

 

Áp dụng BĐT Cô–si cho ba số không âm, kết hợp điều kiện (1) ta có:

$(a+b)+(b+c)+(c+a)\ge 3\sqrt[3]{(a+b)(b+c)(c+a)}=3\Rightarrow a+b+c\ge \dfrac{3}{2} \ \ \ (2)$

Áp dụng BĐT Cô–si cho hai số không âm, kết hợp điều kiện (1) ta có:

$\left\{ \begin{align}   & a+b\ge 2\sqrt{ab} \\  & b+c\ge 2\sqrt{ac} \\  & c+a\ge 2\sqrt{ca} \\ \end{align} \right.$

$\Rightarrow 1=(a+b)(b+c)(c+a)\ge 8abc\Rightarrow abc\le \dfrac{1}{8} \ \ \ (3)$

Biến đổi (1), chú ý 2 bất đẳng thức (2) và (3), ta được:

$\begin{align}   & (a+b)(b+c)(c+a)=1 \\  & \Leftrightarrow (a+b)(bc+ba+{{c}^{2}}+ca)=1 \\  & \Leftrightarrow (a+b)(bc+ba+ca)+a{{c}^{2}}+b{{c}^{2}}=1 \\  & \Leftrightarrow (a+b)(ab+bc+ca)+c(ab+bc+ca)-abc=1 \\  & \Leftrightarrow (a+b+c)(ab+bc+ca)-abc=1 \\  & \Leftrightarrow ab+bc+ca=\dfrac{1+abc}{a+b+c}\le \dfrac{1+\dfrac{1}{8}}{3}=\dfrac{3}{4} \\ \end{align}$

Dấu bằng xảy ra khi $a = b = c = \dfrac{1}{2}.$

 

 

 

 

 

 

Bài 4 (3 điểm)

 

Cho tam giác ABC nhọn nội tiếp (O) . Các đường cao AM, BN, CP cắt nhau tại H. Gọi Q là điểm bất kỳ trên cung nhỏ BC. Gọi E, F là điểm đối xứng của Q qua AB, AC.

1) CMR: MH.MA = MP.MN

2) CMR : E, F, H thẳng hàng.

3) Gọi J là giao điểm của QE và AB. Gọi I là giao điểm của QF và AC. Tìm vị trí của Q trên cung nhỏ BC để $\dfrac{AB}{QJ}+\dfrac{AC}{QI}$ nhỏ nhất.

 

 

Giải

 

 

 

 

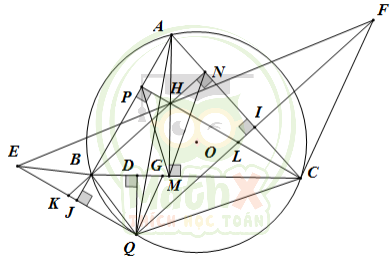
1) CMR: MH.MA = MP.MN

1) Xét tứ giác ANMB có $\widehat {ANB} = \widehat {AMB} = 90^o$ nên nó là tứ giác nội tiếp

⇒ $\widehat {BAM} = \widehat {BNM}$ hay $\widehat {PAM} = \widehat {HNM}$   (1)

Xét tứ giác CNHM có

$\widehat {HNC} + \widehat {HMC} = 90^o + 90^o = 180^o$ nên nó là tứ giác nội tiếp

=> $\widehat {NHM} + \widehat {NCM} = 180^o$    (2)

Tứ giác APMC có $\widehat {APC} = \widehat {AMC} = 90^o$  nên là tứ giác nội tiếp

⇒ $\widehat {APM} + \widehat {ACM} = 180^o$     (3)

Từ (2) và (3)

⇒ $\widehat {NHM} = \widehat {APM}$    (4)

Từ (1) và (4)

⇒ ∆NHM ~ ∆APM (g.g)

$\Rightarrow \dfrac{NM}{AM}=\dfrac{HM}{PM}\Rightarrow MH.MA=MN.MP.$

 

 

2) CMR : E, F, H thẳng hàng.

Gọi K là giao BH và QE, L là giao CH và QF.

Tứ giác AJQI có $\widehat {AIQ} + \widehat {AJQ} = 90^o + 90^o = 180^o$   nên là tứ giác nội tiếp

⇒ $\widehat {JAI} + \widehat {JQI} = 180^o$ 

Mà $\widehat {JAI} + \widehat {BQC} = 180^o$ (do ABQC là tứ giác nội tiếp) nên $\widehat {JQI} = \widehat {BQC} \Rightarrow \widehat {BQE} = \widehat {CQF}$  (5)

Vì E, F đối xứng với Q qua AB, AC nên BQ = BE, CQ = CF

⇒ ∆ BEQ và ∆ CQF cân

=> $\widehat {CQF} = \widehat {CFQ}$    (6) .

Từ (5) và (6) suy ra $\widehat {CFL} = \widehat {BQK}$     (7)

Ta có LH // QK (cùng vuông góc AB); KH // QL (cùng vuông góc AC) nên QKHL là hình bình hành

⇒ $\widehat {QKH} = \widehat {QLH} = \widehat {FLC}$  hay $\widehat {QKB} = \widehat {FLC}$      (8)

Từ (7) và (8)

⇒∆QKB ~ ∆FLC (g.g)

=> $\dfrac{QK}{FL}=\dfrac{QB}{FC}$

Hai tam giác cân BQE và CFQ đồng dạng, nên

$\dfrac{QB}{FC}=\dfrac{QE}{QF}\Rightarrow \dfrac{QK}{FL}=\dfrac{QE}{QF}\Rightarrow \dfrac{QK}{QE}=\dfrac{FL}{FQ}$

Mà QK = LH (do QKHL là hình bình hành) nên

$\dfrac{LH}{QE}=\dfrac{FL}{FQ}$

Vì LH’ // QE nên theo định lý Ta–lét ta có:

$\dfrac{LH'}{QE}=\dfrac{FL}{FQ}$

Do đó LH = LH’

⇒ H’ ≡ H

⇒ H ∈ EF

⇒ H, E, F thẳng hàng.

 

3) Gọi J là giao điểm của QE và AB. Gọi I là giao điểm của QF và AC. Tìm vị trí của Q trên cung nhỏ BC để $\dfrac{AB}{QJ}+\dfrac{AC}{QI}$ nhỏ nhất.

Vẽ QD ⊥ BC tại D. Trên cạnh BC lấy điểm G sao cho

$\widehat {CQG} = \widehat {BQA} \Rightarrow \widehat {BQG} = \widehat {CQA}$

Vì ABQC là tứ giác nội tiếp nên  $\widehat {BAQ} = \widehat {GCQ}$

=> ∆BAQ ~ ∆GCQ (g.g)

=> $\dfrac{BA}{GC}=\dfrac{AQ}{CQ}$

Vì $\widehat {JAQ} = \widehat {DCQ}$  ; $\widehat {QJA} = \widehat {QDC} = 90^o$ 

=> ∆JAQ ~ ∆DCQ (g.g)

=>$\dfrac{AQ}{CQ}=\dfrac{JQ}{DQ}$

Do đó

$\dfrac{BA}{GC}=\dfrac{JQ}{DQ}\Rightarrow \dfrac{AB}{QJ}=\dfrac{GC}{DQ}$

Chứng minh tương tự ta có

:$\begin{align}   & \dfrac{AC}{QI}=\dfrac{GB}{DQ} \\  & \Rightarrow \dfrac{AB}{QJ}+\dfrac{AC}{QI}=\dfrac{GC+GB}{DQ}=\dfrac{BC}{DQ} \\ \end{align}$

Vì BC không đổi nên $\dfrac{AB}{QJ}+\dfrac{AC}{QI}$ nhỏ nhất

⇔ DQ lớn nhất

⇔ Q là điểm chính giữa cung BC nhỏ của đường tròn (O).

 

 

Bài 5 (1 điểm)

 

Chứng minh tồn tại các số nguyên a, b, c sao cho $0 < \left| a+b\sqrt{2}+c\sqrt{3} \right| < \dfrac{1}{1000}$

 

 

Giải:

 

Chứng minh tồn tại các số nguyên a, b, c sao cho $0 < \left| a+b\sqrt{2}+c\sqrt{3} \right| < \dfrac{1}{1000}$

 

Xét nửa khoảng A = (0;1]. Chia nửa khoảng này thành 1000 nửa khoảng

${{A}_{1}}=\left( 0;\dfrac{1}{1000} \right],{{A}_{2}}=\left( \dfrac{1}{1000};\dfrac{2}{1000} \right],...,{{A}_{n}}=\left( \dfrac{n-1}{1000};\dfrac{n}{1000} \right],...,{{A}_{1000}}=\left( \dfrac{999}{1000};1 \right]$

 

Xét bộ số

${{x}_{1}};{{x}_{2}};...;{{x}_{1001}}$ với $\ {{x}_{k}}=\left[ 1-k\sqrt{2} \right]+k\sqrt{2}(k\in \mathbb{N}*,k\le 1001)$

Với mọi k ta có

$-k\sqrt{2}<\left[ 1-k\sqrt{2} \right]\le 1-k\sqrt{2}$  (tính chất phần nguyên) nên  $0<\left[ 1-k\sqrt{2} \right]+k\sqrt{2}\le 1\Rightarrow {{x}_{k}}\in A$

⇒ x_k thuộc một trong các 1000 khoảng A₁, A₂,..., A₁₀₀₀

Có 1001 số x_k mà có 1000 nửa khoảng, do đó tồn tại 2 số  ${{x}_{i}},{{x}_{j}}$ thuộc cùng một nửa khoảng A_m nào đó $0\le |{{x}_{i}}-{{x}_{j}}|<\dfrac{1}{1000}.$

Đặt $a=\left[ 1-i\sqrt{2} \right]-\left[ 1-j\sqrt{2} \right],b=i-j=>{{x}_{i}}-{{x}_{j}}=a+b\sqrt{2}+0.\sqrt{3}$

Mà a là số nguyên, $b\sqrt{2}$ là số vô tỷ nên $a+b\sqrt{2}\ne 0\Rightarrow |{{x}_{i}}-{{x}_{j}}|>0$

Do đó

$0<|{{x}_{i}}-{{x}_{j}}|<\dfrac{1}{1000}\Rightarrow 0<\left| a+b\sqrt{2}+0.\sqrt{3} \right|<\dfrac{1}{1000}$

Vậy tồn tại các số nguyên a, b, c thỏa mãn đề bài.

 

 

Trên đây MATHX đã hướng dẫn các em giải đề thi tuyển sinh lớp 10 môn toán chuyên trường THPT  Chuyên Hà Nội Amsterdam năm học 2015 2016.

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.

 

Phụ huynh và các em học có thể tham khảo một số đề thi vào lớp 10 khác tại đây:

PHÂN TÍCH CHI TIẾT ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN THÀNH PHỐ HÀ NỘI 2023

Đề thi tuyển sinh lớp 10 Trường THPT Chuyên Sư Phạm năm 2023

Đề thi thử vào lớp 10 THPT chuyên Đại học Sư Phạm Hà Nội năm 2023 lần 3