
Mathx.vn biên soạn gửi tới các em hướng dẫn giải đề thi thử vào lớp 10 môn toán trường THPT Chu Văn An Thái Nguyên năm học 2024 2025. Các em học sinh nhấn vào nút tải tài liệu bên dưới để tải đề về làm trước ra giấy sau đó so sánh kết quả và cách giải chi tiết trong bài viết này để đạt được hiệu quả ôn tập tốt nhất. Chúc các em học tốt và đạt kết quả cao trong kì thi THPT sắp tới!!
Môn thi: Toán
Thời gian làm bài: 120 phút
Không sử dụng máy tính cầm tay, tính giá trị của biểu thức
\(A=2\sqrt{3}-4\sqrt{27}+5\sqrt{48}\)
Giải
\(A=2\sqrt{3}-4\sqrt{27}+5\sqrt{48} \\ = 2\sqrt{3}-12\sqrt{3}+20\sqrt{3} \\ = 10\sqrt{3}\)
Không sử dụng máy tính cầm tay, giải hệ phương trình:
\(\left\{ \begin{array}{*{35}{l}} 2x + y = 4 \\ 3x + 2y = 7 \\ \end{array} \right.\)
Giải
Từ phương trình 2x + y = 4 ta suy ra được y = 4 - 2x
Thay vào phương trình dưới ta có phương trình sau
\(3x + 2(4 - 2x) = 7 \\ \Leftrightarrow 3x + 8 - 4x = 7 \\ \Leftrightarrow x = 1 \\ \Rightarrow y = 4 - 2 \times 1 = 2\)
Vậy hệ có nghiệm duy nhất (x;y) = (1;2)
Cho hàm số \(y=f(x)=\left({\sqrt{2}}-1\right)x+3\)
a. Hàm số đã cho đồng biến hay nghịch biến trên \(R\) ? Vì sao?
b. Chứng minh \(f(\sqrt{2}+1)\) là một số tự nhiên
Giải
a. Xét phương trình hàm số có dạng y = ax + b
Ta có: \(a = \sqrt{2}-1 > 0\) nên hàm số đã cho đồng biến trên \(R\)
b. Ta có:
\(f(\sqrt{2}+1) = (\sqrt{2}-1)(\sqrt{2}+1) + 3 = 2 - 1 + 3 = 4\)
Vậy \(f(\sqrt{2}+1)\) là một số tự nhiên
Tìm tọa độ giao điểm của hai đồ thị hàm số \(y = -2x^2\) và \(y = x-3\)
Giải
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số \(y = -2x^2\) và \(y = x-3\) là:
\(-2x^2 = x-3 \Leftrightarrow 2x^2 +x - 3 = 0 \\ \Leftrightarrow \left[ \begin{array}{*{35}{l}} x=1 \\ x=-\dfrac {3}{2} \\ \end{array} \right.\)
+. Với x = 1 ta có y = -2
+. Với \(x = -\dfrac {3}{2}\) ta có \(y = -\dfrac {9}{2}\)
Vậy hai đồ thị hàm số cắt nhau tại \(A(1;-2)\) và \(B(-\dfrac {3}{2};-\dfrac {9}{2})\)
Cho biểu thức \(P=\left({\dfrac{1}{\sqrt{x+4}}}+{\dfrac{1}{\sqrt{x}-4}}\right){\dfrac{\sqrt{x}+4}{\sqrt{x}}}\) với \(x > 0; x \neq 16\)
a. Hãy rút gọn biểu thức P
b. Tính giá trị biểu thức P khi \(x = 4 + 2\sqrt {3}\)
Giải:
a.
\(P=\left({\dfrac{1}{\sqrt{x+4}}}+{\dfrac{1}{\sqrt{x}-4}}\right){\dfrac{\sqrt{x}+4}{\sqrt{x}}} \\ = {\dfrac{2{\sqrt{x}}}{({\sqrt{x}}+4)({\sqrt{x}}-4)}}{\dfrac{{\sqrt{x}}+4}{\sqrt{x}}} \\ ={\dfrac{2}{\sqrt{x-4}}}\)
b.
Ta có \(x = 4 + 2\sqrt {3} = 3 + 2\sqrt {3} . 1 + 1 = (\sqrt {3} + 1)^2\)
Khi \(x = 4 + 2\sqrt {3}\) ta có:
\(P={\dfrac{2}{\sqrt{x}-4}} \\ ={\dfrac{2}{\sqrt{\left({\sqrt{3}}+1\right)^{2}}-4}} \\ ={\dfrac{2}{\sqrt{3}-3}}\)
Trong ngày thứ nhất, hai tổ sản xuất của một xí nghiệp dệt được \(800 m^2\) vải. Ngày thứ hai do cải tiến kĩ thuật nên tổ I đã dệt vượt mức 20% so với ngày thứ nhất; tổ II đã dệt vượt mức 15% so với ngày thứ nhất nên ngày thứ hai cả hai tổ dệt được 945 m2 vải. Hỏi ngày thứ nhất mỗi tổ dệt được bao nhiêu mét vuông vải?
Giải:
Gọi số mét vuông vải mà tổ I và tổ II dệt được trong ngày thứ nhất lần lượt là x và y (0 < x, y < 800)
Tổng số vải hai tổ dệt được trong ngày thứ nhất là: \(x + y = 800 \ \ \ \ (1)\)
Ngày thứ hai tổ I dệt vượt mức: \(x.20\% (m^2)\) nên số vải ngày thứ hai tổ I dệt được là:
\(x+x.20\% = x + \dfrac {1}{5}x = \dfrac {6}{5}x (m^2)\)
Ngày thứ hai tổ II dệt vượt mức: \(15\% .y (m^2)\) nên số vải ngày thứ hai tổ II dệt được là:
\(y+15\% .y = y + \dfrac {3}{20}y = \dfrac {23}{20}y (m^2)\)
Tổng số mét vuông vải hai tổ dệt được trong ngày thứ hai là:
\(\dfrac {6}{5}x + \dfrac {23}{20}y = 945 \ \ \ \ (2)\)
Từ (1) và (2) ta có hệ phương trình bậc nhất hai ẩn x và y :
\(\left\{ \begin{array}{*{35}{l}} x + y = 800 \\ \dfrac {6}{5}x + \dfrac {23}{20}y = 945 \\ \end{array} \right.\)
Giải hệ phương trình trên ta được
\(\left\{ \begin{array}{*{35}{l}} x = 500 \\ y = 300 \\ \end{array} \right.\) (tm)
Vậy trong ngày thứ nhất, tổ I dệt được \(500 m^2\) vải và tổ II dệt được \(300 m^2\) vải.
Cho tam giác ABC vuông tại A, đường cao AH . Biết AB = 6cm và AH = 4,8cm . Tính độ dài cạnh BC và diện tích tam giác ABC
Giải:
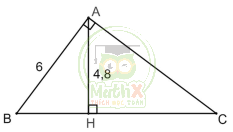
Theo định lý Pitago, ta có:
\(AB^2 = AH^2 + BH^2 \\ \Rightarrow BH^2 = AB^2 - AH^2 = 6^2 - 4,8^2 = 12,96 = 3,6^2\)
=> \(BH = 3,6 cm\)
Ta có: \(AB^2 = BH.BC \Rightarrow BC = \dfrac {AB^2}{BH} = \dfrac {6^2}{3,6} = 10 cm\)
=> \(S_{ABC} = \dfrac {1}{2} BC.AH = \dfrac {1}{2} 10. 4,8 = 24 (cm^2)\)
Cho tam giác ABC vuông tại A, đường cao AH. Từ H kẻ HM vuông góc với AB tại M, HN vuông góc với AC tại N. Chứng minh AM.AB = AN.AC
Giải:
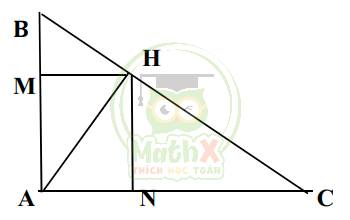
Xét tam giác ABH vuông tại H có đường cao HM
Ta có: \(AM.AB = AH^2\) (1)
Hoàn toàn tương tự ta chứng minh được:
\(AN.AC = AH^2\) (2)
Từ (1) và (2)
=> \(AM.AB=AN.AC\)
Cho đường tròn (O;R), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC (B, C là hai tiếp điểm) với đường tròn. Kẻ đường kính COD của đường tròn (O;R). Tia phân giác của góc \(\widehat {BOD}\) cắt AB tại E .
a. Chứng minh ED là tiếp tuyến của đường tròn (O;R)
b. Tính số đo \(\widehat {AOE}\)
Giải:
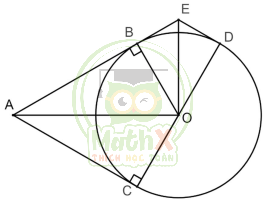
a.
Xét \(\Delta {OBE}\) và \(\Delta {ODE}\) ta có:
OE là cạnh chung
\(\widehat {BOE} = \widehat {DOE}\) (giả thiết)
\(OB = OD\) (đều là bán kính đường tròn (O) )
=> \(\Delta {OBE} = \Delta {ODE}\) (c.g.c)
=> \(\widehat {OBE} = \widehat {ODE}\)
Ta có \(\widehat {OBE} = 90^o\) (tính chất của tiếp tuyến) nên suy ra \(\widehat {ODE} = 90^o\)
Đường thẳng ED đi qua điểm D của đường tròn (O) và \(ED\perp OD\) nên ED là tiếp tuyến của đường tròn (O)
b.
Theo tính chất của hai tiếp tuyến cắt nhau, ta có
OA là tia phân giác của góc \(\widehat {BOC}\)
OE là tia phân giác của góc \(\widehat {BOD}\)
2 góc \(\widehat {BOC}\) và \(\widehat {BOD}\) là 2 góc kề bù
=> \(\widehat {AOE} = 90^o\)
Cho tam giác \(\Delta {ABC}\) nhọn có AB < AC và nội tiếp đường tròn (O). Gọi H là chân đường cao hạ từ đỉnh A của tam giác ABC và E là hình chiếu vuông góc của điểm B lên đường thẳng AO.
a. Chứng minh bốn điểm A, E, H, B cùng thuộc một đường tròn.
b. Gọi M là trung điểm của cạnh BC . Tính tỉ số \(\dfrac {ME}{MH}\)
Giải
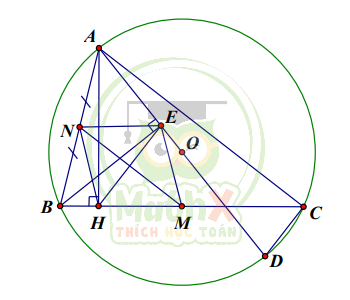
a.
Ta có: \(AH\perp BC\) (gt) => \(\widehat {AHB} = 90^o\)
\(BE\perp AO\) (gt) => \(\widehat {AEB} = 90^o\)
=> \(\widehat {AEB} = \widehat {AHB} = 90^o\)
=> E, H cùng thuộc đường tròn đường kính AB
Vậy 4 điểm A, E, H, B cùng thuộc một đường tròn
b.
Kẻ đường kính AD của đường tròn (O)
Ta có: \(\widehat {BAE} + \widehat {BHE} = 180^o\)
\(\widehat {EHC} + \widehat {BHE} = 180^o\) (2 góc bù nhau)
=> \(\widehat {BAE} = \widehat {EHC}\) (1)
Ta lại có:
\(\widehat {BAE} = \widehat {BAD} = \widehat {BCD}\) (2) (hai góc nội tiếp cùng một đường tròn cùng chắn một cung)
Từ (1) và (2)
=> \(\widehat {EHC} = \widehat {BCD}\) => HE // CD (3)
Mà: \(\widehat {ACD} = 90^o\) (góc nội tiếp chắn nửa đường tròn)
=> \(AC\perp CD\) (4)
Từ (3) và (4)
=> \(HE\perp AC\) (đpcm)
Gọi N là trung điểm của cạnh AB. Khi đó ta có:
Do M là trung điểm của cạnh BC
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Mà \(HE\perp AC\) (cmt)
=> \(HE\perp MN\) (5)
Ta lại có:
\(NE=NH=\dfrac {1}{2}AB\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> N thuộc trung trực của đoạn thẳng HE (6)
Từ (5) và (6)
=> MN là trung trực của đoạn thằng HE
=> \(MH = ME \)
=> \(\dfrac {ME}{MH} = 1\)
Vậy \(\dfrac {ME}{MH} = 1\)
Trên đây MATHX đã hướng dẫn các em giải đề thi thử vào lớp 10 môn toán trường THPT Chu Văn An Thái Nguyên năm học 2024 2025.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
Phụ huynh và các em học có thể tham khảo một số đề thi vào lớp 10 khác tại đây:
PHÂN TÍCH CHI TIẾT ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN THÀNH PHỐ HÀ NỘI 2023
GIẢI ĐỀ THI THỬ VÀO LỚP 10 LẦN 1 TRƯỜNG THPT SƠN TÂY NĂM HỌC 2024-2025
GIẢI ĐỀ THI THỬ VÀO LỚP 10 LẦN 1 PHÒNG GDĐT THỊ XÃ THÁI HÒA NĂM HỌC 2024-2025
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX