GIẢI ĐỀ THI THỬ VÀO LỚP 10 LẦN 1 TRƯỜNG THPT SƠN TÂY NĂM HỌC 2024-2025 - MATHX

 

Nhằm giúp các bạn ôn luyện và giành được kết quả cao trong kì thi tuyển sinh vào lớp 10 môn Toán. MATHX.VN giới thiệu đến các em học sinh lớp 9 đề thi thử môn Toán tuyển sinh vào lớp 10 THPT Sơn Tây lần 1 năm học 2024 – 2025. Đề thi có đáp án và các dạng bài tập hay có trong đề thi vào lớp 10 môn Toán với phương pháp giải chi tiết. Hi vọng tài liệu này sẽ giúp các em học sinh ôn luyện, củng cố kiến thức và chuẩn bị tốt cho kì thi tuyển sinh vào lớp 10 môn Toán.

 

Phụ huynh và các em học sinh tham khảo thêm một số nội dung về ôn thi vào lớp 10 tại đây:

 

LUYỆN TẬP ONLINE: TUYỂN TẬP 50 CÂU HỎI TRẮC NGHIỆM THI VÀO 10 2024 2025 ĐỀ 01 - MATHX

TỔNG HỢP CÁC BÀI TOÁN ĐẠT ĐIỂM 10 THI VÀO LỚP 10 THPT TRÊN TOÀN QUỐC

CHUYÊN ĐỀ TỔNG HỢP ĐỀ THI VÀO LỚP 10 QUA CÁC NĂM

HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN CHUYÊN SỞ GDĐT HÀ NỘI NĂM HỌC 2023 2024 - MATHX

 

 

Để đạt được hiệu quả ôn tập tốt nhất, các em nhấn vào nút bên dưới để tải đề về làm trước sau đó so sánh với lời giải và đáp số trong bài

 

 

 

 

 

GIẢI ĐỀ THI THỬ VÀO LỚP 10 TRƯỜNG THPT SƠN TÂY (LẦN 1)

Năm học 2024-2025

Môn thi: Toán
Thời gian làm bài: 120 phút

 

 

Bài I (2 điểm)

 

Cho các biểu thức \(A={\dfrac{\sqrt{x}-2}{x}}\) và \(B=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{x}{x-4}\) với x >, x ≠ 4.

 

1. Tính giá trị của biểu thức A khi x = 16

 

2. Chứng minh \(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\,\)

 

3. Tìm điều kiện của m để phương trình A.B = m có nghiệm.

 

Lời giải: 

 

1. Thay x =16 (tmđk) vào biểu thức A ta có \(A={\dfrac{\sqrt{16}-2}{16}}\,.\)

 

\(A={\dfrac{1}{8}}\)

 

2. Rút gọn biểu thức B với điều kiện x > 0, x ≠ 4

 

\(B=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{x}{x-4}\)

 

\(={\dfrac{\sqrt{x}-2+{\sqrt{x}}+2+x}{\left({\sqrt{x}}-2\right)\left({\sqrt{x}}+2\right)}}={\dfrac{x+2{\sqrt{x}}}{\left({\sqrt{x}}-2\right)\left({\sqrt{x}}+2\right)}}={\dfrac{{\sqrt{x}}\left({\sqrt{x}}+2\right)}{\left({\sqrt{x}}-2\right)\left({\sqrt{x}}+2\right)}}={\dfrac{{\sqrt{x}}}{{\sqrt{x}}-2}}\)

 

3. Ta có \(A B={\dfrac{\sqrt{x}}{x}}={\dfrac{1}{\sqrt{x}}}\) nên AB = m suy ra \(\dfrac{1}{\sqrt{x}}=m\)

 

Do x >, x ≠ 4 nên phương trình (1) có nghiệm khi \(m\gt 0;m\neq\dfrac{1}{2}\,\)

 

Vậy \(m\gt 0;m\neq\dfrac{1}{2}\,\)thì phương trình AB = m có nghiệm.

 

 

 

 

Bài II (2 điểm)

 

1. Giài bài toán sau bằng cách lập phương trinh hoặc hệ phuơng trình: Một mảnh đất hình chữ nhật có chu vi 90 m. Nếu giảm chiều dài đi 4 m và tăng chiều rộng lên 5 m thi diện tích mảnh đất tăng lên 70\(m^2\) . Tỉnh diện tích mảnh đất hình chữ nhật ban đầu.

 

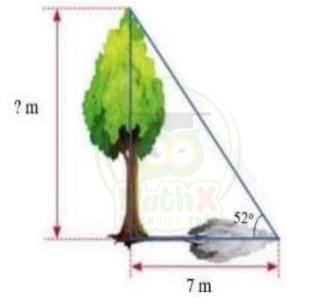
2. Khi mặt trời chiếu qua đỉnh ngọn cây thì góc tạo bởi tia nắng mặt trời với mặt đất là 52 và bóng cây trên mặt đất dài 7 m. Tính chiều cao của cây (kết quả lấy đến hai chữ số của phần thập phân).

 

 

Lời giải: 

 

1) Gọi chiều dài và chiều rộng lần lượt là x và y (đơn vị m; x > y > 0)

 

Vì chu vi mảnh đất hình chữ nhật là 90m nên ta có phương trình \(2\left(x+y\right)=90\) hay x + y = 45

 

Do giảm chiều dài 4m và tăng chiều rộng 5m thì diện tích tăng thêm 70\(m^2\) nên ta có phương trình

 

\(\left(x-4\right)\!\left(y+5\right)=x y+70\) hay 5x - 4y = 90

 

Ta có hệ phương trình \(\left\{ \begin{array}{}   x + y = 45  \\    5x - 4y = 90 \\ \end{array} \right.\) <=> \(\left\{ \begin{array}{}   x = 30\\    y = 15\\ \end{array} \right.\) (tmđk)

 

Vậy chiều dài là 30 m chiều rộng là 15 m. Diện tích mảnh đất hình chữ nhật ban đầu là 30.15 = 450\(m^2\).

 

2) Chiều cao của cây là 7.tan\(52^o\)

 

Vậy chiều cao của cây là 7.tan\(52^o\) ≈ 8,96 (m)

 

 

 

Bài III (2,5 điểm)

 

1. Giải hệ phương trình \(\left\{ \begin{array}{}    2{\sqrt{x}}+{\dfrac{3}{y-1}}=1  \\    3{\sqrt{x}}-{\dfrac{6}{y-1}}=5 \\ \end{array} \right.\)

 

2. Trong mặt phẳng tọa độ Oxy, cho parabol \(\left(P\right):y=x^{2}\) và đường thẳng \(\left(d\right):y=m x+2m-1\,.\)

 

a) Khi m = 2 tìm tọa độ giao điểm của (P) và d.

 

b) Với giá trị nào của m thì khoảng cách từ gốc tọa độ O đến đường thẳng d bằng 2.

 

Lời giải: 

 

1) Điều kiện x ≥ 0, y ≠ 1.

 

\(\left\{ \begin{array}{}    2{\sqrt{x}}+{\dfrac{3}{y-1}}=1  \\    3{\sqrt{x}}-{\dfrac{6}{y-1}}=5 \\ \end{array} \right.\)

 

Đặt \(a={\sqrt{x}}{\big(}a\geq0{\big)},b={\dfrac{1}{y-1}}{\big(}b\neq0{\big)}\) hệ phương trình trở thành \(\left\{ \begin{array}{}    2a + 3b = 1  \\    3a-6b=5 \\ \end{array} \right.\)

 

Giài hệ phương trình tìm được \(\left\{ \begin{array}{}    a =1  \\    b=-{\dfrac{1}{3}} \\ \end{array} \right.\)

 

Đối chiếu điều kiện ta được nghiệm của hệ phương trình là (x,y) = (1;2)

 

2)

 

a) Khi m = 2 ta có \(\left(d\right):y=2x+3\)

 

Phương trình hoành độ giao điểm của đường thẳng d và Parabol (P) là \(x^{2}=2x+3\) ⇔ \(x^{2}-2x-3=0\)

 

Ta có Δ' = 1 + 3 = 4 > 0 nên phương trình có hai nghiệm x = -1; x = 3

 

Với x =−1 thì y =1

 

Với x = 3 thì y = 9

 

Vậy với m = 2 thì d cắt (P) tại hai điểm có tọa độ là (−1;1), (3;9 )

 

b) \((d):y=m x+2m-1\)

 

Nếu m = 0 thì \((d)\colon y=-1\). Khi đó khoàng cách từ điểm O đến đường thẳng d là -1 Suy ra m = 0 không thỏa mãn.

 

Với m ≠ 0 ta có \((d):y=m x+2m-1\), d cắt trục Ox tại điểm M \(M\!\left(-{\dfrac{2m-1}{m}};0\right)\) và d cắt trục Oy tại điềm N (0;2m - 1). Suy ra \(O M=\left|{\dfrac{2m-1}{m}}\right|\); \({{ON}}=\left|2m-1\right|\)

 

Nếu \(m={\dfrac{1}{2}}\) ta có \(\left(d\right):y={\dfrac{1}{2}}x\) là đường thẳng đi qua O nên khoảng cách từ O đến d bằng 0 .

 

Nếu \(m≠{\dfrac{1}{2}}\) theo hệ thức lượng trong tam giác vuông, khoảng cách từ điểm O đến d là h thỏa mãn

 

\(\dfrac{1}{h^{2}}=\dfrac{1}{O M^{2}}+\dfrac{1}{O N^{2}}.\)

 

Khoảng cách từ điểm O đến d bằng 2 thì h = 2 suy ra

 

\({\dfrac{1}{4}}={\dfrac{1}{O M^{2}}}+{\dfrac{1}{O N^{2}}}\) ⇔ \({\dfrac{1}{4}}={\dfrac{m^{2}}{\left(2m-1\right)^{2}}}+{\dfrac{1}{\left(2m-1\right)^{2}}}\)

 

⇔ \(4m^{2}+4=4m^{2}-4m+1\) ⇔ \(m=-{\dfrac{3}{4}}\left(\mathrm{tm}\right)\)

 

Vậy \(m=-{\dfrac{3}{4}}\) thì khoảng cách từ điểm O đến đường thẳng d bằng 2 .

 

 

 

 

Bài IV (3 điểm)

 

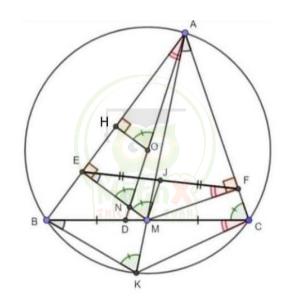
Cho tam giác ABC (AB> AC) nội tiếp đường tròn tâm O. Gọi M là trung điểm của đoạn thẳng BC; E F, lần lượt là chân đường vuông góc kẻ từ M đến các đường thẳng AB,AC , .

 

1. Chứng minh tứ giác AEMF là tứ giác nội tiếp

 

2. Đường thẳng AM cắt đường tròn (O) tại điểm thứ hai là K. Chứng minh KBC = MEF và BC.ME = EF.BK

 

3. Đường thẳng AO cắt cạnh BC tại D. Gọi J là trung điểm của đoạn thẳng EF. Chứng minh AD // JM

 

Lời giải: 

 

1) Ta có:

 

\(A E M=90^{\circ}\)

 

\(A F M=90^{\circ}\)

 

Tứ giác AEMF nội tiếp đường tròn đường kính AM

 

2) Xét đường tròn (O) có KBC = KAC

 

 

Xét đường tròn đường kính AM : MEF = KAC

Suy ra KBC = MEF

 

Chứng minh tương tự KBC = MFE

 

Suy ra hai tam giác ∆KCB và ∆MFE đồng dạng nên BC.ME = EF.BK

 

3) Do M là trung điểm của đoạn thẳng BC, J là trung điểm của đoạn thẳng EF nên ∆MEJ và ∆KBM đồng dạng. Suy ra JME = MKB = AKB

 

Gọi H là trung điểm của AB, N là giao điểm của EM và AD

 

Ta có AKB = AOH \((=\dfrac{1}{2}sd AB)\); AOH = ANE (đồng vị). Suy ra AKB = ANE

 

Vì D ≠ M và JME = ANE nên AD // JM

 

 

 

 

Bài V (0,5 điểm) Cho a,b,c là các số thực không âm thỏa mãn a + b + c = 1 . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = ac + bc - 2024ab.

 

Lời giải: 

 

* GTLN: \(P=a c+b c-2024a b=c{\big(}a+b{\big)}-2024a b\leq c{\big(}a+b{\big)}\leq{\dfrac{(a+b+c)^{2}}{4}}={\dfrac{1}{4}}.\)

 

 

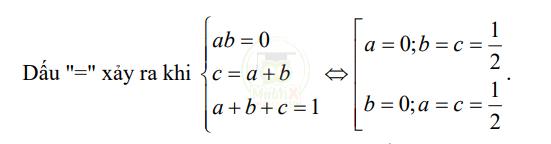
Vậy giá trị lớn nhất của biểu thức P là \(\dfrac{1}{4}\) ⇔ a = 0; b = c = \(\dfrac{1}{2}\) hoặc \(b=0;a=c={\dfrac{1}{2}}\)

 

* GTNN: \(P=a c+b c-2024a b\geq c\left(a+b\right)-2024{\dfrac{\left(a+b\right)^{2}}{4}}\geq-2024{\dfrac{\left(a+b\right)^{2}}{4}}=-506(a+b)^{2}.\)

 

Vì a +  b + c = 1 và a,b,c không âm nên a + b ≤ 1. Suy ra \(P\geq-506(a+b)^{2}\geq-506\)

 

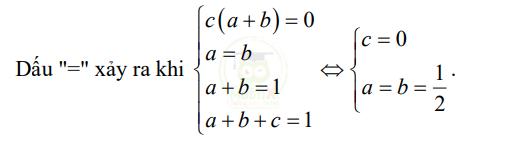
Vậy giá trị nhỏ nhất của biểu thức P là -506 ⇔ c = 0; a = b = \(\dfrac{1}{2}\)

 

 

 

Như vậy MATHX đã cùng các em đi giải đề thi thử vào 10 lần 1 THPT Sơn Tây năm học 2024 - 2025. Hy vọng các em học sinh nắm được nội dung kiến thức, tham khảo được các dạng bài và thành công trong kì thi tuyển sinh sắp tới!