Trường Toán Online MATHX
Những năm gần đây, cấu trúc chung của đề thi tuyển sinh lớp 10 môn toán thường ít có sự thay đổi. Đây là điều kiện thuận lợi để các em học sinh có thể ôn tập tốt hơn, giảm bớt phần nào gánh nặng thi cử đối với các em. Với mục đích giúp học sinh có kế hoạch ôn luyện và từ đó đạt điểm tốt trong bài thi, thầy/cô MATHX sẽ phân tích chi tiết đề thi tuyển sinh lớp 10 môn Toán thành phố Hà Nội năm học 2023 - 2024 để các bạn có thể tham khảo và chuẩn bị kiến thức, ôn tập tốt hơn.
Hình thức: Thi tự luận
Thời gian làm bài: 120 phút
Thang điểm: 10 điểm
Cấu trúc đề thi tuyển sinh vào lớp 10 môn Toán: bao gồm 70% câu hỏi ở mức độ nhận biết và thông hiểu, 30% là vận dụng và vận dụng cao.
Nội dung: gồm 5 bài như sau
Nội dung: Bài toán gồm từ 2 đến 3 ý liên quan đến biểu thức chứa căn bậc hai
Những năm gần đây, bài này thường có 2 ý, một ý thuộc phần thông hiểu, học sinh cần nắm vững kiến thức là có thể giải quyết được bài toán này, ý thứ hai thuộc phần vận dụng thấp, cũng không quá khó khi ta đọc kĩ đề và học tập thật cẩn thận về các nội dung kiến thức dưới đây.
Nội dung kiến thức (chọn trong các phần kiến thức dưới đây)
- Các bài toán thực tế: chuyển động, công việc, lãi suất,…
- Các bài có liên quan đến hình học: ứng dụng thực tế của hệ thức lượng; hình học không gian,…
- Các bài toán tích hợp liên môn: liên quan đến phần Vật Lý, Hóa Học,…
- Giải hệ phương trình (quy về hệ phương trình bậc nhất hai ẩn, hai phương trình, dạo gần đây thường sử dụng phương pháp đặt ẩn phụ, ý này thường chiếm từ 0,5 đến 1 điểm tùy theo từng năm) hoặc giải phương trình.
- Bài toán về hàm số bậc hai, phương trình bậc hai, đồ thị, giao điểm của hai đồ thị, hệ thức Vi-ét và ứng dụng. Ở phần này thường có một ý phân hóa ở mức độ vận dụng, thường có 2 ý chiếm khoảng 1 đến 1,5 điểm.
Bài này thường có 3 ý, phân hóa theo cấp độ từ thấp đến cao. Mỗi ý thường từ 0,5 đến 1,5 điểm
Các nội dung hay gặp
- Chứng minh nhiều điểm cùng thuộc một đường tròn
- Chứng minh tứ giác nội tiếp
- Tính độ dài đoạn thẳng, tính góc, chứng minh hệ thức hình học và các biểu thức liên quan (thường dùng cả phần kiến thức về "Hệ thức lượng trong tam giác vuông và ứng dụng thực tế" và "Tam giác đồng dạng")
- Tiếp tuyến của đường tròn và các bài toán liên quan đến tiếp tuyến
- Chứng minh ba đường thẳng đồng quy, hai đường thẳng song song, vuông góc, điểm thuộc đường thẳng cố định, bài toán quỹ tích, cực trị hình học…
- Chứng minh ba điểm thẳng hàng..
Đặc biệt lưu ý: Trong bài hình, phải chú trọng đến hình vẽ, ta cần vẽ hình chính xác theo đúng yêu cầu bài toán. KHÔNG có hình vẽ, KHÔNG có điểm TOÀN BỘ câu này.
Nội dung thường chọn một trong các phần sau:
- Chứng minh bất đẳng thức
- Tìm giá trị lớn nhất (GTLN), tìm giá trị nhỏ nhất (GTNN)
- Giải hệ phương trình, phương trình nâng cao,…
Đây thường là câu khó nhất trong đề thi, hay được gọi là "câu điểm 10"
Đây là một đề thi nhẹ nhàng, không đánh đố, không gây áp lực, tương thích với diễn biến ôn thi trực tuyến, thi vào 10 trong điều kiện kèm theo phòng chống dịch Covid-19 của học sinh.
Mặc dù đền nhẹ nhàng nhưng đề cũng có tính phân loại thí sinh tương đối tốt. Câu hỏi phân loại thí sinh là câu II. 2 bài toán về tương giao của đường thẳng và parabol, ý thứ 2 của câu 2 bài IV và bài V .
Xem thêm: TUYỂN TẬP CÁC ĐỀ THI VÀO THPT 10 CHUYÊN CÁC TỈNH THÀNH
Đề môn Toán đáp ứng được yêu cầu kiểm tra đánh giá học sinh và có yếu tố phân hóa ở câu I ý c, ý b của câu III.2, ý c câu IV, câu V. Hàm lượng kiểm tra kiến thức và kỹ năng cơ bản cao, không đánh đố học sinh. Học sinh chỉ cần có thời gian ôn luyện, thực hành giải tốt các dạng toán cơ bản và làm bài cẩn thận thì hoàn toàn có thể hoàn thành đề thi một cách nhanh chóng.
Câu I. (2 điểm)
Cho hai biểu thức 
1) Tính giá trị của biểu thức A khi
2) Chứng minh
3) Tìm tất cả giá trị của x để A.B = 4.
a) (0,5 điểm)
Phân tích
Đây là dạng toán tính giá trị biểu thức khi biết giá trị của biến số.
Hướng dẫn
Thay 
Vậy với
b) (1 điểm)
Phân tích
Đề bài của ý này là chứng minh nhưng thực chất là chúng ta chỉ việc thu gọn biểu thức B. Và câu này đã cho chúng ta kết quả của việc thu gọn chính là biểu thức cần chứng minh.
Hướng dẫn
Với 
Vậy với 
c) (0,5 điểm)
Phân tích
Câu này chúng ta vận dụng phương pháp giải phương trình, tìm giá trị của x để thỏa mãn yêu cầu bài toán và ý này không thực sự là quá khó.
Hướng dẫn
Ta có:
A.B = 4
Vậy với thì A.B = 4.
Câu II. (2 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Theo kế hoạch, một phân xưởng phải làm xong 900 sản phẩm trong một số ngày quy định. Thực tế, mỗi ngày phân xưởng đã làm được nhiều hơn 15 sản phẩm so với số sản phẩm phải làm trong một ngày theo kế hoạch. Vì thế 3 ngày trước khi hết thời hạn, phân xưởng đã làm xong 900 sản phẩm. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải làm bao nhiêu sản phẩm? (Giả định số sản phẩm mà phân xưởng làm được tròn mỗi ngày là bằng nhau)
2) Một khối gỗ dạng hình trụ có bán kính đấy là 30 cm và chiều cao là 120cm. Tính thể tích của khối gỗ đó (lấy 
1) (2 điểm)
Phân tích
Đây là dạng bài toán về công việc.
Theo đề bài ta có bảng sau:
|
Năng suất |
Công việc |
Thời gian |
|
|
Kế hoạch |
x |
900 |
|
|
Thực tế |
x + 15 |
900 |
|
Phương trình:
Hướng dẫn
Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là 
Thời gian để phân xưởng đó làm xong 900 sản phẩm theo kế hoạch là: 
Thực tế, mỗi ngày phân xưởng làm được: 
Thời gian thực tế để phân xưởng đó làm xong 900 sản phẩm là: 
Vì thực tế, phân xưởng đã làm xong 900 sản phẩm trước thời hạn 3 ngày nên ta có phương trình:
Suy ra:
Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm xong 60 sản phẩm.
2) (0,5 điểm)
Phân tích
Với bài này các em học sinh cần nhớ công thức tính thể tích hình trụ:
Hướng dẫn
Theo đề bài ta có: hình trụ có bán kính đáy R = 30 cm, chiều cao h = 120 cm.
Vậy thể tích của khối gỗ hình trụ là:
Câu III: 2,5 điểm
1) Giải hệ phương trình
2) Trong mặt phẳng toạ độ Oxy, cho parabol 
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt.
b) Gọi 
1) (1 điểm)
Phân tích
Để giải hệ phương trình này ta sử dụng phương pháp đặt ẩn phụ và phương pháp thế hoặc cộng đại số
Hướng dẫn
ĐK:
Đặt, 
Giải hệ ta được:
Từ v = 2, ta thay lại tính được 
Vậy hệ phương trình có nghiệm .
2) (1 điểm)
a) (0,5 điểm)
Phân tích
Đây là bài toán về giao điểm của hai đồ thị.
Hướng dẫn
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
Phương trình có 
Suy ra phương trình (1) luôn có hai nghiệm phân biệt.
Vậy (d) luôn cắt (P) tại hai điểm phân biệt (đpcm).
b)(0,5 điểm)
Phân tích
Sử dụng hệ thức Vi-ét để giải quyết bài toán này.
Hướng dẫn
Áp dụng hệ thức Vi-ét ta có:
Điều kiện:
Ta có:
Thay (2) và (3) ta có:
Vậy với m = -1 thì hoành độ giao điểm của (d) và (P) thỏa mãn
Câu IV. (3 điểm)
Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn (O). Tiếp tuyến tại điểm A của đường tròn (O) cắt đường thẳng BC tại điểm S. Gọi I là chân đường vuông góc kẻ từ điểm O đến đường thẳng BC.
1) Chứng minh tứ giác SAOI là tứ giác nội tiếp.
2) Gọi H và D lần lượt là chân các đường vuông góc kẻ từ điểm A đến các đường thẳng SO và SC. Chứng minh .\(\widehat {OAH}=\widehat {IAD}\)
3) Vẽ đường cao CE của tam giác ABC. Gọi Q là trung điểm của đoạn thẳng BE. Đường thẳng QD cắt đường thẳng AH tại điểm K. Chứng minh BQ . BA = BD . BI và đường thẳng CK song song với đường thẳng SO.
1)(1 điểm)
Phân tích
Sử dụng dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có tổng hai góc đối bằng 180O
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm này chính là tâm của đường tròn ngoại tiếp tứ giác đó.
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới 1 góc α.
- Tứ giác đó là một trong các hình sau: hình chữ nhật, hình vuông, hình thang cân.
Hướng dẫn
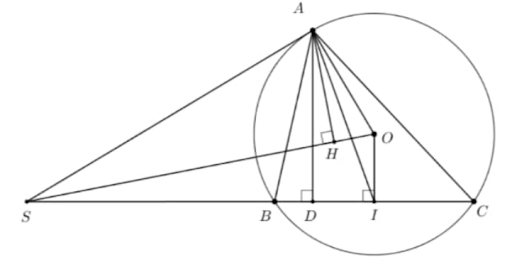
Do SA là tiếp tuyến của (O) nên 
Xét tứ giác SAOI có:
Mà 2 góc này ở vị trí đối diện nên tứ giác SAOI nội tiếp (dhnb) (đpcm)
b) (1 điểm)
Phân tích
Bài này chúng ta sử dụng tính chất của tứ giác nội tiếp.
Hướng dẫn
Do 
Tương tự 
\(\widehat {OAH} = \widehat {ASO}\)(do cùng phụ với \(\widehat {AOH}\) )
Do tứ giác SAOI nội tiếp ( chứng minh trên) nên \(\widehat {ASO} = \widehat {AIO}\) ( góc nội tiếp cùng chắn cung AO)
\(=>\widehat {OAH} = \widehat {AIO} (=ASO)\)
Do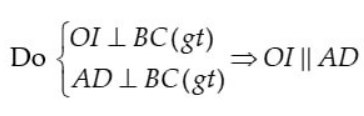 
(từ vuông góc đến song song).
\(=>\widehat {AIO} = \widehat {IAD}\)(cặp góc so le trong)
\(=>\widehat {OAH}=\widehat {IAD}(=\widehat {AIO})\)(đpcm)
c) (1 điểm)
Phân tích
Bài này là dạng toán nâng cao, ý 1: sử dụng hai tam giác đồng dạng để chứng minh tỉ lệ này, còn ý 2: sử dụng định lý từ vuông góc đến song song để chứng minh hai đường thẳng CK và SO song song với nhau.
Hướng dẫn
Bài 5. (0,5 điểm)
Cho hai số thực dương a và b thỏa mãn 
Phân tích
Đây là dạng toán nâng cao từ 9,5 lên 10 điểm. Thường những dạng chứng minh bất đẳng thức chúng ta sẽ sử dụng bất đẳng thức AM – GM hoặc bất đẳng thức Bunyakovsky.
Hướng dẫn
Cách 1: Bất đẳng thức cần chứng minh tương đương với
Hay
Sử dụng bất đẳng thức AM – GM, ta có
Suy ra 
Ta có điều phải chứng minh. Dấu bằng xảy ra khi và chỉ khi
Cách 2: Sử dụng bất đẳng thức Bunyakovsky:
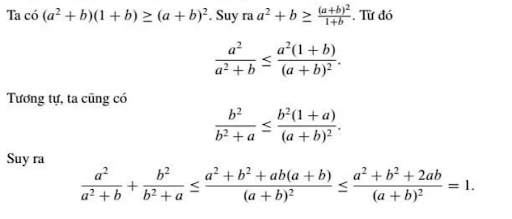
Xem thêm: ĐỀ THI THỬ VÀO 10 THCS VÀ THPT LƯƠNG THẾ VINH 2023 - 2024 mới nhất (có đáp án kèm lời giải)
Vừa rồi, thầy cô MATHX đã phân tích chi tiết cấu trúc đề, các dạng bài toán cũng như hướng dẫn giải chi tiết đề tuyển sinh vào lớp 10 môn Toán của thành phố Hà Nội năm học 2023 - 2024. Chúc các em ôn tập tốt, chuẩn bị thật tốt và thành công trong kỳ thi vào lớp 10 sắp tới.
