GIẢI ĐỀ THI THỬ VÀO LỚP 10 LẦN 1 PHÒNG GDĐT THỊ XÃ THÁI HÒA NĂM HỌC 2024-2025 - MATHX

 

Kì thi tuyển sinh vào lớp 10 đang đến gần. Nhằm giúp các em học sinh ôn tập và chuẩn bị thật tốt cho kì thi sắp tới đội ngũ MATHX biên soạn tài liệu giải đề thi thử vào lớp 10 lần 1 phòng giáo dục và đào tạo thị xã Thái Hòa năm học 2024-2025. Chúc các em học tốt!

 

Phụ huynh và các em học sinh tham khảo thêm một số nội dung về ôn thi vào lớp 10 tại đây:

 

LUYỆN TẬP ONLINE: TUYỂN TẬP 50 CÂU HỎI TRẮC NGHIỆM THI VÀO 10 2024 2025 ĐỀ 01 - MATHX

TỔNG HỢP CÁC BÀI TOÁN ĐẠT ĐIỂM 10 THI VÀO LỚP 10 THPT TRÊN TOÀN QUỐC

CHUYÊN ĐỀ TỔNG HỢP ĐỀ THI VÀO LỚP 10 QUA CÁC NĂM

 

 

Để đạt được hiệu quả ôn tập tốt nhất, các em nhấn vào nút bên dưới để tải đề về làm trước sau đó so sánh với lời giải và đáp số trong bài

 

 

 

 

GIẢI ĐỀ THI THỬ VÀO LỚP 10 LẦN 1 PHÒNG GDĐT THỊ XÃ THÁI HÒA NĂM HỌC 2024-2025 - MATHX

 

 

 

Câu 1: (2,5 điểm)

 

1) Tính giá trị của biểu thức \(A=\sqrt{27}-\sqrt{12}+\dfrac{1}{5}\sqrt{75}.\)

 

2) Rút gọn biểu thức \(B=\left({\dfrac{1}{x-2{\sqrt{x}}}}+{\dfrac{1}{\sqrt{x}-2}}\right)\colon{\dfrac{\sqrt{x}+1}{x-4{\sqrt{x}}+4}},\) với x > 0 và x ≠ 4

 

3) Xác định các hệ số a, b của hàm số y = ax + b , biết rằng đồ thị của hàm số đi qua điểm C (1;4) và song song với đường thẳng y = 2x - 1.

 

Lời giải: 

 

1) Tính giá trị của biểu thức \(A=\sqrt{27}-\sqrt{12}+\dfrac{1}{5}\sqrt{75}.\)

 

\(A=3\sqrt3-2\sqrt3+\dfrac13.5\sqrt3\)

 

\(=2\sqrt3\)

 

2) Rút gọn biểu thức \(B=\left({\dfrac{1}{x-2{\sqrt{x}}}}+{\dfrac{1}{\sqrt{x}-2}}\right)\colon{\dfrac{\sqrt{x}+1}{x-4{\sqrt{x}}+4}},\) với x > 0 và x ≠ 4

 

\(=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}-2\right)^{2}}{\left(\sqrt{x}+1\right)}\)

 

\(={\dfrac{{\sqrt{x}}-2}{\sqrt{x}}}.\)

 

3) Xác định các hệ số a, b của hàm số y = ax + b, biết rằng đồ thị của hàm số đi qua điểm C (1;4) và song song với đường thẳng y = 2x - 1.

 

Vì đồ thị của hàm số song song với đường thẳng y = 2x - 1 nên \(\left\{ \begin{array}{}    a =2  \\    b ≠ -1 \\ \end{array} \right.\)

 

Vì đồ thị của hàm số đi qua điểm C (1;4) và a = 2 nên ta có: 4 = 2.1 + b ⇔ b = 2 (TM). Vậy a = 2 và b = 2.

 

 

 

 

Câu 2: (2,0 điểm)

 

1) Giải phương trình \(3x^{2}-5x-8=0.\)

 

2) Cho phương trình \(x^{2}-4x-1=0\) có hai nghiệm \(x_1, x_2\). Không giải phương trình, hãy tính giá trị của biểu thức \(P={\bigl(}2x_{1}+1{\bigr)}{\bigl(}x_{2}^{\ 2}+1{\bigr)}.\)

 

Lời giải: 

 

1) Giải phương trình \(3x^{2}-5x-8=0.\)

 

Phương trình \(2x^{2}-5x-7=0.\) có a = 3, b = −5 , c = −8

 

nên \(a-b+c=3-\left(-5\right)+\left(-8\right)=0\)

 

Do đó phương trình có hai nghiệm là \(x_1 = -1\)

 

và \(x_{2}={\dfrac{-c}{a}}={\dfrac{-\left(-8\right)}{3}}={\dfrac{8}{3}}\)

 

2) Cho phương trình \(x^{2}-4x-1=0\) có hai nghiệm \(x_1, x_2\). Không giải phương trình, hãy tính giá trị của biểu thức \(P={\bigl(}2x_{1}+1{\bigr)}{\bigl(}x_{2}^{\ 2}+1{\bigr)}.\)

 

Vì phương trình có hai nghiệm \(x_1, x_2\) nên theo hệ thức Vi-ét ta có \(\left\{ \begin{array}{}    x_1 + x_2 =4  \\    x_1 . x_2=-1 \\ \end{array} \right.\)

 

Vì \(x_2\) là nghiệm của phương trình \(x^{2}-4x-1=0\) nên \(x_2^2 -4x_2 - 1= 0\)

 

⇔ \(x_{2}^{\ 2}+1=4x_{2}+2.\)

 

Do đó \(P=2\left(2x_{1}+1\right)\left(2x_{2}+1\right)\)

 

\(=2\Bigl[4x_{1}x_{2}+2\bigl(x_{1}+x_{2}\bigr)+1\Bigr]=2\Bigl[4\bigl(-1\bigr)+2.4+1\bigr]=10.\)

 

 

 

 

Câu 3: (2,0 điểm) 

 

1) Hai lớp 9A và 9B có tổng cộng 95 học sinh. Trong đợt quyên góp vở ủng hộ các bạn học sinh nghèo, bình quân mỗi bạn lớp 9A ủng hộ 3 quyển, mỗi bạn lớp 9B ủng hộ 4 quyển. Vì vậy cả hai lớp đã ủng hộ được 330 quyển. Tính số học sinh của mỗi lớp.

 

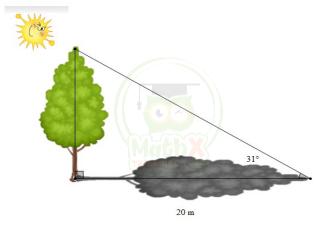
2) Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 31° và bóng của một cây trên mặt đất dài 20 m (xem hình vẽ bên). Tính chiều cao của cây (làm tròn kết quả đến mét).

 

 

Lời giải: 

 

1) Hai lớp 9A và 9B có tổng cộng 95 học sinh. Trong đợt quyên góp vở ủng hộ các bạn học sinh nghèo, bình quân mỗi bạn lớp 9A ủng hộ 3 quyển, mỗi bạn lớp 9B ủng hộ 4 quyển. Vì vậy cả hai lớp đã ủng hộ được 330 quyển. Tính số học sinh của mỗi lớp.

 

Gọi số học sinh mỗi lớp 9A, 9B lần lượt là x, y (học sinh).

 

Điều kiện: x y, ∈ N* và x y < 95

 

Vì hai lớp 9A và 9B có tổng cộng 95 học sinh nên ta có phương trình: x + y = 95 (1)

 

Số vở của lớp 9A ủng hộ là 3x (quyển), số vở của lớp 9B ủng họ là 4y (quyển)

 

Vì cả hai lớp đã ủng hộ được 330 quyển nên ta có phương trình: \(3x+4y=330.\) (2)

 

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{}    x + y = 95  \\    3x + 4y = 330 \\ \end{array} \right.\) Giải hệ phương trình tìm được x  = 50 (TM) và y = 45 (TM)

 

Vậy số học sinh lớp 9A là 50 học sinh, số học sinh lớp 9B là 45 học sinh.

 

2) Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 31° và bóng của một cây trên mặt đất dài 20 m (xem hình vẽ bên). Tính chiều cao của cây (làm tròn kết quả đến mét).

 

 

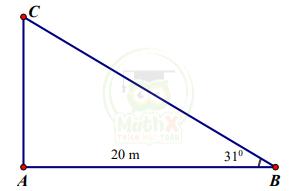
Gọi chiều cao của cây là AC, bóng của cây trên mặt đất là AB. Xét ∆ABC vuông tại A có: AC = AB.tan31°

 

⇒ AC ≈ 12 (m). Vậy cây cao 12m.

 

 

 

 

Câu 4: (3,0 điểm) Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm). Trên cung nhỏ BC lấy điểm D sao cho CD < BD, tia AD cắt đường tròn (O) tại điểm thứ hai là E. Gọi I là trung điểm của DE và K là giao điểm của BC và DE.

 

1) Chứng minh ABOI là tứ giác nội tiếp.

 

2) Chứng minh \({\widehat{O IB}}={\widehat{O M C}}\) và AK.AI = AD.AE

 

3) Qua D kẻ đường thẳng song song với AB, đường thẳng này cắt BC tại điểm M. Đường thẳng ME lần lượt cắt đường tròn (O) và đường thẳng AB tại các điểm P và N (P khác E). Chứng minh rằng \({\widehat{APN}}={\widehat{ICB}}\)

 

Lời giải: 

 

1) Chứng minh ABOI là tứ giác nội tiếp.

 

 

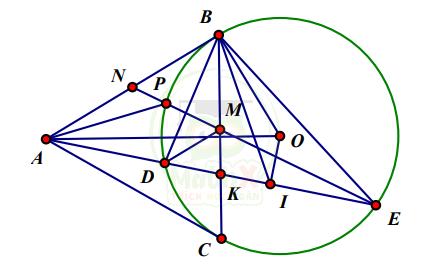
Vì AB là các tiếp tuyến của đường tròn (O) nên ta có AB ⊥ OB ⇒ \({\widehat{{ABO}}}=90^{\circ}\)

 

Vì I là trung điểm của DE nên OI ⊥ DE (theo mối quan hệ giữa đường kính và dây) ⇒ \({\widehat{{AIO}}}=90^{\circ}\)

 

Xét tứ giác ABOI có \({\widehat{{A B O}}}+{\widehat{{A I O}}}=90^{\circ}+90^{\circ}\) = \(180^o\)

 

Do đó ABOI là tứ giác nội tiếp.

 

2) Chứng minh \({\widehat{O IB}}={\widehat{O M C}}\) và AK.AI = AD.AE

 

Vì ABOI là tứ giác nội tiếp nên \({\widehat{O IB}}={\widehat{O AB}}\)

 

Mà theo tính chất của hai tiếp tuyến cắt nhau ta có \({\widehat{O AC}}={\widehat{O AB}}\) .Từ đó suy ra \({\widehat{O IB}}={\widehat{O AC}}\)

 

Xét ∆ACD và ∆AEC có: \({\widehat{CAD}}\) chung và \({\widehat{ACD}}={\widehat{AEC}}\) (cùng bằng \(\cfrac{1}{2}\) sđ CD) nên ∆ACD ☐ ∆AEC (g.g) ⇒ \({\dfrac{A C}{A E}}={\dfrac{A D}{A C}}\) ⇒ \(A C^{2}=A E.A D.\) (1)

 

Ta có \({\widehat{A B O}}={\widehat{{A C O}}}={\widehat{{A I O}}}=90^{\circ}\) nên năm điểm A , B , O , I , C cùng thuộc đường tròn đường kính AO => \({\widehat{AIC}}={\widehat{ABC}}\) = \(\widehat{ACB}\)

 

Xét ∆AIC và ∆ACK có: \({\widehat{IAC}}\) chung và \({\widehat{AIC}}={\widehat{ABC}}\) (theo chứng minh trên) nên ∆AIC ☐ ∆ACK (g.g) => \({\dfrac{A I}{A C}}={\dfrac{A C}{A K}}\Rightarrow A I.A K=A C^{2}.\ \ (2)\)

 

Từ (1) và (2) suy ra AK.AI = AD.AE

 

3) Qua D kẻ đường thẳng song song với AB, đường thẳng này cắt BC tại điểm M. Đường thẳng ME lần lượt cắt đường tròn (O) và đường thẳng AB tại các điểm P và N (P khác E). Chứng minh rằng \({\widehat{APN}}={\widehat{ICB}}\)

 

 

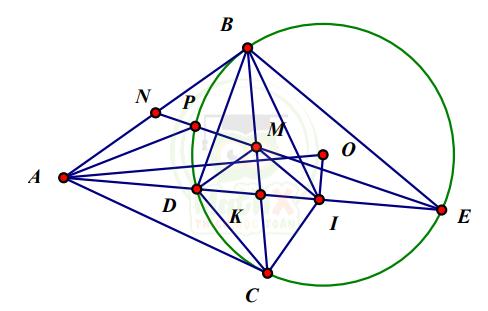
Vì AN DM // nên theo hệ quả của định lí Thales ta có 

 

\({\dfrac{A N}{A E}}={\dfrac{D M}{D E}}\ \ (1)\)

 

Ta có ∆ABE ☐ ∆ADB (g.g) => \({\dfrac{A B}{A E}}={\dfrac{A D}{A B}}\quad(2)\)

 

Vì AB // DM ⇒ \({\widehat{DMC}}={\widehat{ABC}}\) = \({\widehat{ACB}}\), mà \({\widehat{AIC}}={\widehat{ACB}}\) (chứng minh ở câu b)

 

\({\widehat{DMC}}={\widehat{AIC}}\) => DMIC là tứ giác nội tiếp => \({\widehat{MID}}={\widehat{MCD}}=\widehat{ABD}\)

 

Xét ∆ABD và ∆DIM có \({\widehat{MID}}={\widehat{ABD}}\) (theo chứng minh trên) và \({\widehat{BAD}}={\widehat{DMI}}\) (hai góc đồng vị) ⇒ ∆ABD ☐ ∆DIM (g.g)

 

=> \({\dfrac{A D}{A B}}={\dfrac{D M}{D I}}={\dfrac{2D M}{D E}}\cdot~(3)\)

 

Từ (1); (2) và (3) suy ra \({\dfrac{A B}{A E}}={\dfrac{2A N}{A E}}\Longrightarrow A B=2A N\Rightarrow A N=B N.\) (4)

 

Dễ dàng chứng minh được \(B N^{2}=N P.N E.\ \ (5)\)

 

Từ (4) và (5) suy ra \(A N^{2}=N P.N E ⇒\dfrac{A N}{N E}=\dfrac{N P}{A N}\) ⇒ ∆ANE ☐ ∆PNA (c.g.c)

 

⇒ \({\widehat{{A P N}}}={\widehat{{E A N}}}\Rightarrow{\widehat{{A P N}}}={\widehat{{I C B}}}\) (do ABIC là tứ giác nội tiếp ⇒ \({\widehat{ICB}}={\widehat{EAN}}\)

 

 

 

 

Câu 5: (0,5 điểm) Giải phương trình \(2x^{2}-3x+{\dfrac{4}{9}}={\sqrt{3x-{\dfrac{1}{3}}}}-{\sqrt{2x^{2}+{\dfrac{1}{9}}}}.\)

 

Lời giải: 

 

Điều kiện: \(3x-{\dfrac{1}{3}}\geq0⇔ x\geq{\dfrac{1}{9}}\,\)

 

Ta có \(2x^{2}-3x+{\dfrac{4}{9}}={\sqrt{3x-{\dfrac{1}{3}}}}-{\sqrt{2x^{2}+{\dfrac{1}{9}}}}.\)

 

⇔ \(\left(2x^{2}+\dfrac{1}{9}\right)-\left(3x-\dfrac{1}{3}\right)+\left(\sqrt{2x^{2}+\dfrac{1}{9}}-\sqrt{3x-\dfrac{1}{3}}\right)=0\)

 

⇔ \(\left({\sqrt{2x^{2}+{\dfrac{1}{9}}}}\right)^{2}-\left({\sqrt{3x-{\dfrac{1}{3}}}}\right)^{2}+\left({\sqrt{2x^{2}+{\dfrac{1}{9}}}}-{\sqrt{3x-{\dfrac{1}{3}}}}\right)=0\)

 

⇔ \(\left(\sqrt{2x^{2}+\dfrac{1}{9}}-\sqrt{3x-\dfrac{1}{3}}\right)\left(\sqrt{2x^{2}+\dfrac{1}{9}}+\sqrt{3x-\dfrac{1}{3}}+1\right)=0\)

 

⇔ \(\left({\sqrt{2x^{2}+{\dfrac{1}{9}}}}-{\sqrt{3x-{\dfrac{1}{3}}}}\right)=0\) (vì \({\sqrt{2x^{2}+{\dfrac{1}{9}}}}+{\sqrt{3x-{\dfrac{1}{3}}}}+1\gt 0\) với mọi \(x\geq{\dfrac{1}{4}})\)

 

⇔ \(\sqrt{2x^{2}+\dfrac{1}{9}}=\sqrt{3x-\dfrac{1}{3}}⇔2x^{2}-3x+\dfrac{4}{9}=0\) ⇔ \(\left\{ \begin{array}{}    x = \dfrac{4}{3} (TM) \\    x = \dfrac{1}{6} (TM)\\ \end{array} \right.\)

 

Vậy tập nghiệm của phương trình là S = \(\left\{{\dfrac{4}{3}};{\dfrac{1}{6}}\right\}\)

 

 

 

 

Như vậy MATHX đã cùng các em đi giải đề thi thử vào 10 lần 1 thị xã Thái Hòa năm học 2024 - 2025. Hy vọng các em học sinh nắm được nội dung kiến thức, tham khảo được các dạng bài và thành công trong kì thi tuyển sinh sắp tới!