SỬ DỤNG PHƯƠNG PHÁP TRUY HỒI ĐỂ GIẢI BÀI TOÁN ĐẾM

Phương pháp truy hồi là một phương pháp khá hữu dụng và được áp dụng rộng dãi, phổ biến với nhiều bài toán. Trong bài viết này chúng ta sẽ cùng thầy Trần Hữu Hiếu sử dụng phương pháp truy hồi đề giải một số bài toán đếm nhé!

SỬ DỤNG PHƯƠNG PHÁP TRUY HỒI ĐỂ GIẢI BÀI TOÁN ĐẾM

Biên soạn: Trần Hữu Hiếu

Bài toán: We want to cover the following 2 x 8 rectangle by using eight 2 x 1 rectangles.

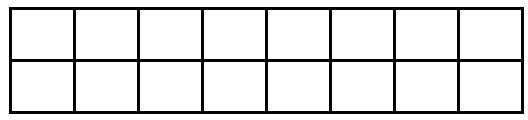
Each 2 x 1 rectangle is placed horizontally or vertically.

How many arrangements are possible to cover the 2 x 8 rectangle?

Dịch đề: Chúng ta muốn phủ kín lưới hình chữ nhật kích thước 2 x 8 bằng cách sử dụng 8 hình chữ nhật kích thước 2 x 1.

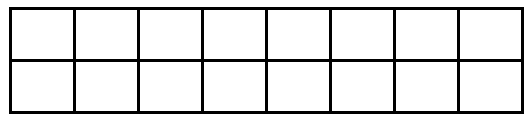
Mỗi hình chữ nhật chỉ được đặt thẳng đứng hoặc nằm ngang.

Hỏi có tất cả bao nhiêu cách sắp xếp để có thể phủ kín lưới hình chữ nhật 2 x 8 ở trên?

Phân tích:

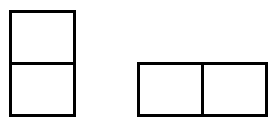
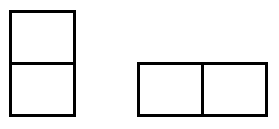
Khi tiếp cận bài toán này, thoạt đầu tiên, chúng ta thường thử một vài cách sắp xếp, và tất nhiên, chúng ta sẽ xuất phát từ các ô vuông bên trái. Ta thấy, ô vuông ở góc trên bên trái có thể được che phủ theo 1 trong 2 cách dưới đây:

Cách 1:

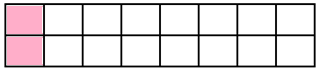
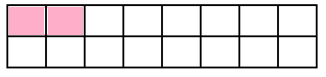
Cách 2:

Với cách 1, ta nhận thấy số cách để phủ kín hình 2 x 8 lúc này chính là số cách để phủ kín hình 2 x 7.

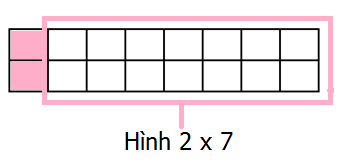
Với cách 2, ta thấy ô vuông góc dưới bên trái cũng được che phủ bởi 1 hình 2 x 1 đặt nằm ngang.

Phần còn lại chính là 1 hình chữ nhật 2 x 6.

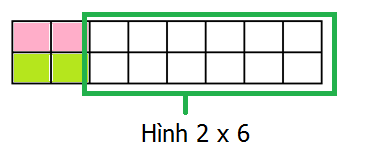
Từ đó ta nghĩ đến việc đi xây dựng cách giải dựa vào việc xây dựng công thức truy hồi để tính số cách che phủ một hình chữ nhật có kích thước 2 x n, trong đó n là số tự nhiên lớn hơn 0.

>>> Tham khảo thêm: [TOÁN LỚP 4,5] CHUYÊN ĐỀ SUY LUẬN LOGIC - PHƯƠNG PHÁP LẬP BẢNG

Lời giải:

Gọi A_k là số cách dùng k hình chữ nhật kích thước 2 x 1 để phủ kín hình chữ nhật 2 x k. (với k là số tự nhiên lớn hơn hoặc bằng 2).

Dễ thấy:

A₁ = 1;

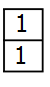
A₂ = 2;

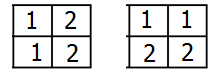
A₃ = 3

Xét hình chữ nhật kích thước 2 x n (n  3)

Xét ô vuông góc trên bên trái của hình 2 x n, ta có 2 khả năng sau:

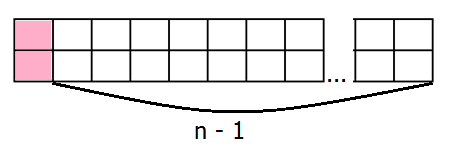
TH1: Ô vuông góc trên bên trái được che bởi hình 2 x 1 đặt thẳng đứng. Khi đó phần còn lại chính là hình 2 x (n – 1)                                                                                              (1)

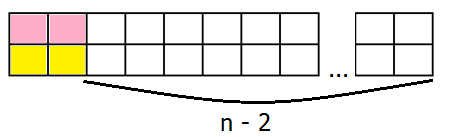
TH2: Ô vuông góc trên bên trái được che bởi hình 2 x 1 nằm ngang, khi đó ô vuông góc dưới bên trái cũng được che bởi hình 2 x 1 nằm ngang. Khi đó phần còn lại chính là hình 2 x (n – 2)   (2)

Từ (1) và (2) ta xây dựng được công thức truy hồi như sau:

            A_n = A_{n – 1} + A_n-2

Từ đó dễ dàng tính viết dược dãy A_n chính là dãy: 1; 2; 3; 5; 8; 13; 21; 34

Đáp án: A₈ = 34

Một số bài toán tương tự:

Bài 1. Có bao nhiêu dãy số gồm toàn các chữ số 1 và 2 và có tổng các số hạng  bằng 15.

Bài 2. Có bao nhiêu số có 8 chữ số, được tạo thành từ các chữ số 1, 2, 3 sao cho không có hai chữ số 1 nào đứng liền nhau.

Bài 3. Có một cầu thang gồm n bậc. Mỗi bước đi có thể bước lên 1 bậc hoặc bước lên 2 bậc. Tìm số các để đi đến bậc thứ n?

Bài 4. a) Cho hình như hình vẽ. Có bao nhiêu cách tô màu các hình tròn bằng 3 màu khác nhau sao cho 2 hình tròn bất kỳ được nối bởi 1 cạnh có màu khác nhau.

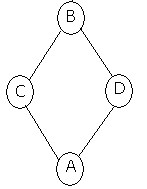
b) Có bao nhiêu cách tô màu 5 đỉnh của hình ngũ giác bằng 3 màu sao cho hai đỉnh được nối với nhau bởi 1 cạnh của ngũ giác thì khác màu nhau.

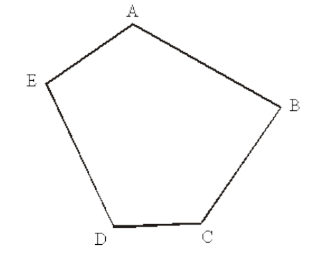
Bài 5. Gọi S_n là số cách tô màu n đỉnh của hình n-giác bằng 3 màu sao cho hai đỉnh được nối với nhau bằng 1 cạnh của đa giác thì khác màu nhau. . Hãy tìm công thức truy hồi để tính S_n.