
Mathx.vn biên soạn gửi tới các em hướng dẫn giải đề thi tuyển sinh lớp 10 môn toán của Sở GDĐT Hà Nội năm học 2023 2024. Các em học sinh nhấn vào nút tải tài liệu bên dưới để tải đề về làm trước ra giấy sau đó so sánh kết quả và cách giải chi tiết trong bài viết này để đạt được hiệu quả ôn tập tốt nhất. Chúc các em học tốt và đạt kết quả cao trong kì thi THPT sắp tới!!
Môn thi: Toán
Thời gian làm bài: 120 phút
Cho hai biểu thức \( A=\dfrac{x+2}{\sqrt{x}}\) và \(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\) với \(x>0,x\ne 1\)
a) Tính giá trị của biểu thức \(A\) khi \(x=9\).
b) Chứng minh \(B=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\).
c) Tìm các giá trị của \(x\) để \(A.B=4\).
Giải
a) Thay \(x=9\) (thỏa mãn điều kiện) vào biểu thức \(A\) ta được:
\(A=\dfrac{9+2}{\sqrt{9}}\Rightarrow A=\dfrac{9+2}{3}=\dfrac{11}{3}\).
Vậy khi \(x=9\) thì \(A=\dfrac{11}{3}\).
b) Với \(x>0,x\ne 1\) ta có:
\(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1} \\ =\dfrac{(2\sqrt{x}-3)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\dfrac{3-\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ =\dfrac{2x+2\sqrt{x}-3\sqrt{x}-3+3-\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ =\dfrac{2x-2\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ =\dfrac{2\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+1)} \\ =\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)
Vậy \(B=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\) (đpcm).
c) Với \(x>0,x\ne 1\) ta có:
\(A.B=\dfrac{x+2}{\sqrt{x}}.\dfrac{2\sqrt{x}}{\sqrt{x}+1}=\dfrac{2x+4}{\sqrt{x}+1} \)
Để \(A.B=4\) thì
\(\dfrac{2x+4}{\sqrt{x}+1}=4 \\ \Leftrightarrow \dfrac{2x+4}{\sqrt{x}+1}=\dfrac{4(\sqrt{x}+1)}{\sqrt{x}+1} \\ \Rightarrow 2x+4=4\sqrt{x}+4\Leftrightarrow 2x-4\sqrt{x}=0 \\ \Leftrightarrow 2\sqrt{x}(\sqrt{x}-2)=0\Leftrightarrow \left[ \begin{array}{*{35}{l}} 2\sqrt{x}=0 \\ \sqrt{x}-2=0 \\ \end{array}\Leftrightarrow \left[ \begin{array}{*{35}{l}} x=0 \\ x=4 \\ \end{array} \right. \right.\)
Đối chiếu với điều kiện ta có \(x=4\) là giá trị cần tìm.
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Theo kế hoạch, một phân xưởng phải làm xong 900 sản phẩm trong một số ngày quy định. Thực tế, mỗi ngày phân xưởng đã làm được nhiều hơn 15 sản phẩm so với số sản phẩm phải làm trong một ngày theo kế hoạch. Vì thế 3 ngày trước khi hết thời hạn, phân xưởng đã làm xong 900 sản phẩm. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phẩm mà phân xưởng làm được trong mỗi ngày là bằng nhau.)
2) Một khối gỗ dạng hình trụ có bán kính đáy là \(30~\,\text{cm}\)và chiều cao là \(120~\,\text{cm}\). Tính thể tích của khối gỗ đó. (lấy \(\pi \approx 3,14\)).
Giải
1) Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là \(x\) (sản phẩm), \(x\in {{\mathbb{N}}^{*}},x<900\).
Thời gian phân xưởng phải hoàn thành theo kế hoạch là \(\dfrac{900}{x}\) (ngày).
Thực tế, mỗi ngày phân xưởng làm được \(x+15\) (sản phẩm).
Thời gian phân xưởng hoàn thành trên thực tế là \(\dfrac{900}{x+15}\) (ngày).
Vì phân xưởng hoàn thành trước thời hạn 3 ngày nên ta có phương trình:
\(\dfrac{900}{x}-\dfrac{900}{x+15}=3\Rightarrow 900(x+15)-900x=3x(x+15) \\ \Leftrightarrow 3{{x}^{2}}+45x-13500=0\Leftrightarrow {{x}^{2}}+15x-4500=0\)
Chú ý: Ôn lại kiến thức, đối với phương trình bậc 2 = 0 ta sẽ sử dụng công thức Delta
\(\Delta = b^2 - 4ac \)
với a, b, c là hệ số của phương trình bậc 2
\(ax^2 + bx + c = 0\)
1. Nếu \(\Delta > 0\), tức là \(b^2 - 4ac > 0\), thì phương trình bậc 2 sẽ có hai nghiệm thực và phân biệt. Bằng cách sử dụng công thức nghiệm của phương trình bậc 2:
\(x_1 = (-b + \sqrt{\Delta})/(2a)\) và \(x_2 = (-b - \sqrt{\Delta})/(2a)\), chúng ta có thể tính được giá trị của hai nghiệm \(x_1\) và \(x_2\).
2. Nếu \(\Delta = 0\), tức là \(b^2 - 4ac = 0\), thì phương trình bậc 2 sẽ có một nghiệm kép. Bằng cách sử dụng công thức nghiệm của phương trình bậc 2:
\(x = -b/(2a)\), chúng ta có thể tính được giá trị của nghiệm kép x.
3. Nếu \(\Delta < 0\), tức là \(b^2 - 4ac < 0\), thì phương trình bậc 2 sẽ không có nghiệm thực. Trong trường hợp này, chúng ta nói phương trình bậc 2 có nghiệm phức.
Áp dụng công thức Delta để giải phương trình trên ta được
\(x=60\) (thoả mãn), \(x=-75\) (loại).
Vậy theo kế hoạch, mỗi ngày phân xưởng phải làm 60 sản phẩm.
2)
Thể tích khối gỗ: \(V=\pi {{r}^{2}}h\approx 3,{{14.30}^{2}}.120=339\,120\,\,\left( ~\text{c}{{\text{m}}^{3}} \right)\)
Vậy thể tích khối gỗ khoảng \(339\,120\,\,\left( ~\text{c}{{\text{m}}^{3}} \right)\)
1) Giải hệ phương trình \(\left\{ \begin{array}{*{35}{l}} \dfrac{2}{x-3}-3y=1 \\ \dfrac{3}{x-3}+2y=8 \\ \end{array} \right.\) .
2) Trong mặt phẳng tọa độ \(Oxy\), cho parabol \((P) : y={{x}^{2}}\) và đường thẳng \((d):y=(m+2)x-m\).
a) Chứng minh \((d)\) luôn cắt \((P)\) tại hai điểm phân biệt.
b) Gọi \({{x}_{1}}\) và \({{x}_{2}}\) là hoành độ các giao điểm của \((d)\) và \((P)\). Tìm tất cả giá trị của \(m\) để
\(\dfrac{1}{{{x}_{1}}}+\dfrac{1}{{{x}_{2}}}=\dfrac{1}{{{x}_{1}}+{{x}_{2}}-2}\) .
Giải
1)
Điều kiện: \(x\ne 3.\)Đặt \(\dfrac{1}{x-3}=a\) hệ phương trình trở thành:
\(\left\{ \begin{array}{*{35}{l}} 2a-3y=1 \\ 3a+2y=8 \\ \end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} a=2 \\ y=1 \\ \end{array} \right. \right.\) .
Với \(a=2\Rightarrow \dfrac{1}{x-3}=2\Rightarrow x=\dfrac{7}{2}\) (thỏa mãn điều kiện).
Vậy hệ phương trình có nghiệm \((x;y)=\left( \frac{7}{2};1 \right)\) .
2)
a) Xét phương trình hoành độ giao điểm \((d)\) và \((P)\).
\({{x}^{2}}=(m+2)x-m\Leftrightarrow {{x}^{2}}-(m+2)x+m=0\,\,\left( * \right)\)
Ta có \(\Delta ={{(m+2)}^{2}}-4.1.m\Rightarrow \Delta ={{m}^{2}}+4\).
Do \({{m}^{2}}\ge 0\) với mọi \(m\Rightarrow {{m}^{2}}+4>0\) với mọi \(m\)
\(\Rightarrow \Delta >0\) với mọi \(m\), phương trình (*) luôn có hai nghiệm phân biệt với mọi \(m\).
Vậy \((d)\) luôn cắt \((P)\) tại hai điểm phân biệt với mọi \(m\).
b) Gọi \({{x}_{1}}\) và \({{x}_{2}}\) là hoành độ các giao điểm của \((d)\) và \((P)\).
Theo hệ thức Vi - et ta có:
\(\left\{ \begin{array}{*{35}{l}} {{x}_{1}}+{{x}_{2}}=m+2 \\ {{x}_{1}}{{x}_{2}}=m \\ \end{array} \right.\).
Điều kiện để biểu thức \(\dfrac{1}{{{x}_{1}}}+\dfrac{1}{{{x}_{2}}}=\dfrac{1}{{{x}_{1}}+{{x}_{2}}-2}\) có nghĩa là:
\(\left\{ \begin{array}{*{35}{l}} {{x}_{1}}\ne 0 \\ {{x}_{2}}\ne 0 \\ {{x}_{1}}+{{x}_{2}}\ne 2 \\ \end{array} \right.\)
Khi đó:
\(\left\{ \begin{array}{*{35}{l}} m+2\ne 2 \\ m\ne 0 \\ \end{array}\Leftrightarrow m\ne 0 \right.\).
Xét: \(\dfrac{1}{{{x}_{1}}}+\dfrac{1}{{{x}_{2}}}=\dfrac{1}{{{x}_{1}}+{{x}_{2}}-2}\)
\(\Leftrightarrow \dfrac{{{x}_{1}}+{{x}_{2}}}{{{x}_{1}}.{{x}_{2}}}=\dfrac{1}{{{x}_{1}}+{{x}_{2}}-2} \\ \Leftrightarrow \dfrac{m+2}{m}=\dfrac{1}{m+2-2} \\ \Leftrightarrow \dfrac{m+2}{m}=\dfrac{1}{m} \\ \Leftrightarrow m+2=1 \\ \Leftrightarrow m=-1\) (thỏa mãn)
Vậy với \(m=-1\) thì thỏa mãn yêu cầu bài toán.
Cho tam giác \(ABC\) có ba góc nhọn \((AB
1) Chúng minh tứ giác \(SAOI\) là tứ giác nội tiếp.
2) Gọi H và D lần lượt là chân các đường vuông góc kẻ từ điểm A đến các đường thẳng SO và SC. Chứng minh \(\widehat{OAH}=\widehat{IAD}\).
3) Vẽ đường cao CE của tam giác ABC. Gọi Q là trung điểm của đoạn thẳng BE. Đường thẳng QD cắt đường thằng AH tại điểm K. Chứng minh \(BQ\cdot BA=BD\cdot BI\) và đường thẳng CK song song với đường thẳng SO.
Giải
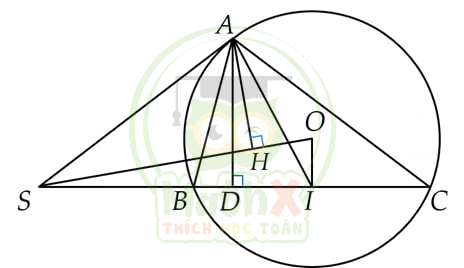
1)
Tứ giác \(SAOI\) có:
\(\widehat{SAO}={{90}^{{}^\circ }}\) (tính chất của tiếp tuyến);
\(\widehat{SIO}={{90}^{{}^\circ }}\,\,\,(OI\bot BC)\);
\(\widehat{SAO}+\widehat{SIO}={{90}^{{}^\circ }}+{{90}^{{}^\circ }}={{180}^{{}^\circ }}\)
Mà \(\widehat{SAO}\) và \(\widehat{SIO}\) đối nhau
\(\Rightarrow \) Tứ giác \(SAOI\) nội tiếp đường tròn đường kính SO.
2)
Theo câu 1), ta có: tứ giác \(SAOI\) nội tiếp nên \(\widehat{SOA}=\widehat{SIA}\) (hai góc nội tiếp cùng chắn \(\overset\frown{SA}\)).
\(\Rightarrow {{90}^{{}^\circ }}-\widehat{SOA}={{90}^{{}^\circ }}-\widehat{SIA}\)
Mà \({{90}^{{}^\circ }}-\widehat{SOA}=\widehat{OAH}\) (vì \(\vartriangle AHO\) vuông tại H) ;
\({{90}^{{}^\circ }}-\widehat{SIA}=\widehat{IAD}\) (vì \(\vartriangle ADI\) vuông tại D)
\(\Rightarrow \widehat{OAH}=\widehat{IAD}\).
3)
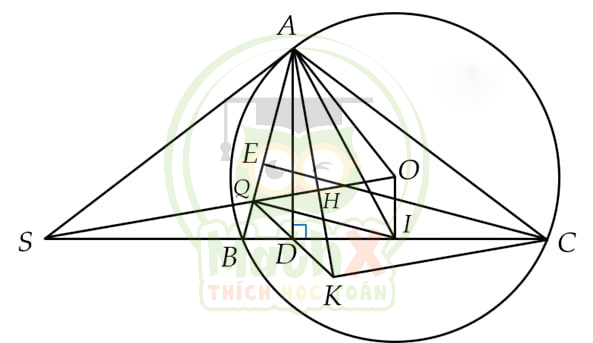
Vì \(OI\bot BC\Rightarrow I\) là trung điểm của BC mà Q là trung điểm của \(BE\Rightarrow IQ\) là đường trung bình của \(\vartriangle BEC\Rightarrow IQ // CE\).
Mà \(CE\bot AB\Rightarrow IQ\bot AB\Rightarrow \widehat{IQA}={{90}^{{}^\circ }}\).
Lại có \(\widehat{IDA}={{90}^{{}^\circ }}\) vì \((AD\bot SC)\)
\(\Rightarrow \) Tứ giác \(AQDI\) nội tiếp đường tròn đường kính \(AI\).
\(\Rightarrow \widehat{QAI}+\widehat{QDI}={{180}^{{}^\circ }}\) và \(\widehat{BDQ}+\widehat{QDI}={{180}^{{}^\circ }}\)(hai góc kề bù)
\(\Rightarrow \widehat{BDQ}=\widehat{QAI}\left( ={{180}^{{}^\circ }}-\widehat{QDI} \right)\).
Xét \(\vartriangle BDQ\) và \(\vartriangle BAI\) có:
\(\hat{B}\) chung;
\(\widehat{BDQ}=\widehat{BAI}\) (chứng minh trên);
\(\Rightarrow \vartriangle BDQ\,\,\sim \,\vartriangle BAI\) (g . g)
\(\Rightarrow \dfrac{BD}{BQ}=\dfrac{BA}{BI}\Rightarrow BQ\cdot BA=BD\cdot BI\).
Vì \(\widehat{BDQ}=\widehat{KDC} \) (hai góc đối đỉnh)
\(\Rightarrow \widehat{KDC}=\widehat{BAI}\) (1);
Ta có: \(\widehat{SAB}+\widehat{BAO}={{90}^{{}^\circ }}\) (vì \(SA\bot OA\)) ;
\(\widehat{DAC}+\widehat{ACD}={{90}^{{}^\circ }}\) (vì \(\vartriangle ADC\) vuông tại D);
\(\widehat{BCA}=\widehat{SAB}\) (góc nội tiếp và góc tạo bời tia tiếp tuyến và dây cung cùng chắn \(\overset\frown{AB}\)).
\(\Rightarrow \widehat{BAO}=\widehat{DAC}\) hay \(\widehat{BAD}=\widehat{OAC}\)
Theo ý 2) ta có
\(\widehat{DAI}=\widehat{HAO} \\ \Rightarrow \widehat{BAI}=\widehat{KAC}\text{ }\) (2);
Từ (1) và (2), ta có:
\(\widehat{KAC}=\widehat{KDC} \)
\(\Rightarrow\) tứ giác \(DKCA\) nội tiếp.
\(\Rightarrow \widehat{ADC}=\widehat{AKC}={{90}^{{}^\circ }}\Rightarrow AK\bot CK\).
Mà \(AK\bot SO\Rightarrow SO // KC\).
Cho hai số thực dương \(a\) và \(b\) thỏa mãn \(a+b\le 2\) . Chứng minh \(\dfrac{{{a}^{2}}}{{{a}^{2}}+b}+\dfrac{{{b}^{2}}}{{{b}^{2}}+a}\le 1\).
Giải:
Ta có \(\dfrac{{{a}^{2}}}{{{a}^{2}}+b}+\dfrac{{{b}^{2}}}{{{b}^{2}}+a}\,\,\le \,\,1\,\,\,\,\left( * \right)\)
\(\Leftrightarrow {{a}^{2}}\left( {{b}^{2}}+a \right)+{{b}^{2}}\left( {{a}^{2}}+b \right)\le \left( {{a}^{2}}+b \right)\left( {{b}^{2}}+a \right)\)
\(\Leftrightarrow 2{{a}^{2}}{{b}^{2}}+\left( {{a}^{3}}+{{b}^{3}} \right)\le {{a}^{2}}{{b}^{2}}+{{a}^{3}}+{{b}^{3}}+ab\)
\(\Leftrightarrow \ {{a}^{2}}{{b}^{2}}-ab\le 0\)
\(\Leftrightarrow \ ab(ab-1)\le 0\Leftrightarrow ab-1\le 0\) (Vì \(a>0,\,\,b>0\) (giả thiết))
\(\Leftrightarrow \ ab\le 1 \left( ** \right)\)
Áp dụng bất đẳng thức Cô si cho hai số dương \(a,\,\,b\) ta có \(a+b\ge 2\sqrt{ab}\).
Mà \(2\ge ab\) (giả thiết) suy ra \(2\ge 2\sqrt{ab}\Leftrightarrow \sqrt{ab}\le 1\Leftrightarrow ab\le 1.\)
Như vậy (**) được chứng minh nên (*) được chứng minh.
Dấu bằng xảy ra khi và chỉ khi \(a=b=1.\)
Trên đây MATHX đã hướng dẫn các em giải đề thi tuyển sinh lớp 10 môn toán của Sở GDĐT Hà Nội năm học 2023 2024.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
Phụ huynh và các em học có thể tham khảo một số đề thi vào lớp 10 khác tại đây:
PHÂN TÍCH CHI TIẾT ĐỀ THI TUYỂN SINH LỚP 10 MÔN TOÁN THÀNH PHỐ HÀ NỘI 2023
Đề thi tuyển sinh lớp 10 Trường THPT Chuyên Sư Phạm năm 2023
Đề thi thử vào lớp 10 THPT chuyên Đại học Sư Phạm Hà Nội năm 2023 lần 3
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX