
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 trong thời gian sắp tới, MATHX biên soạn đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán THCS Nguyễn Tri Phương - Thừa Thiên Huế năm học 2023 - 2024. Hy vọng rằng bài viết này sẽ giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới.
Môn: Toán
Năm học: 2023 - 2024
Câu 1: (2,0 điểm) Tính nhanh
a) Tìm y, biết: \(y \times 2,5 + y \times 3,5 + y \times 4 = 45\)
b) Tính giá trị của biểu thức A:
\(A = 3,4 \times (16,35 - 7,35) + 0,125 \times 3,4 \times 8\)
Hướng dẫn:
a) \(\ \ \ \ \ y \times 2,5 + y \times 3,5 + y \times 4 = 45 \\ \Leftrightarrow y \times (2,5 + 3,5 + 4) = 45 \\ \Leftrightarrow y \times 10 = 45 \\ \Leftrightarrow y = 45 : 10 \\ \Leftrightarrow y = 4,5\)
b) \(\ \ \ \ \ A = 3,4 \times (16,35 - 7,35) + 0,125 \times 3,4 \times 8 \\ \Leftrightarrow A = 3,4 \times 9 + 3,4 \times 0,125 \times 8 \\ \Leftrightarrow A = 3,4 \times 9 + 3,4 \times 1 \\ \Leftrightarrow A = 3,4 \times (9 + 1) \\ \Leftrightarrow A = 3,4 \times 10 \\ \Leftrightarrow A = 34\)
Đáp số:
a) y = 4,5
b) A = 34
Câu 2: (1,5 điểm) Hai kho chứa tất cả 418 tấn thóc, nếu chuyển từ kho thứ nhất sang kho thứ hai 60 tấn thóc thì số thóc ở kho thứ nhất nhiều hơn số thóc ở kho thứ hai là 18 tấn. Tính số thóc ban đầu ở mỗi kho?
Hướng dẫn:
Ta có sơ đồ số thóc ở hai kho sau khi di chuyển là:
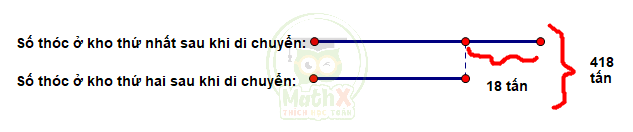
Số thóc ở kho thứ nhất sau khi di chuyển là:
(418 + 18) : 2 = 218 (tấn)
Số thóc ban đầu ở kho thứ nhất là:
218 + 60 = 278 (tấn)
Số thóc ban đầu ở kho thứ hai là:
418 - 278 = 140 (tấn)
Đáp số:
Kho thứ nhất: 278 tấn
Kho thứ hai: 140 tấn
Câu 3: (2,0 điểm) Để tham dự Sea Games 32 ở Cam-pu-chia, Đoàn Việt Nam đã tổ chức lễ xuất quân chia làm nhiều đợt. Đợt thứ nhất có 60% vận động viên xuất quân so với tổng số vận động viên toàn đoàn. Đợt thứ hai có 50% số vận động viên còn lại được xuất quân. Tính số vận động viên đã xuất quân của cả hai đội, biết số vận động viên của đoàn chưa xuất quân là 141 người.
Hướng dẫn:
Theo đề bài, số vận động viên chưa xuất quân chiếm 50% số vận động viên còn lại sau khi xuất quân đợt 1
=> Số vận động viên còn lại sau khi xuất quân đợt 1 là:
\(141 \times 100 : 50 = 282 \) (vận động viên)
Cũng theo đề bài, đợt thứ nhất có 60% vận động viên xuất quân so với tổng số vận động viên toàn đoàn
=> Số vận động viên còn lại sau khi xuất quân đợt 1 chiếm: 100% - 60% = 40% tổng số vận động viên toàn đoàn
=> Số vận động viên toàn đoàn là:
\(282 \times 100 : 40 = 705 \) (vận động viên)
Số vận động viên đã xuất quân là:
\(705 - 141 = 564 \) (vận động viên)
Đáp số: 564 vận động viên
Câu 4: (1,5 điểm) Một ô tô dự định đi từ A đến B trong 3 giờ. Do thời tiết xấu nên vận tốc của ô tô giảm đi 14km/giờ, vì thế ô tô đến B muộn 1 giờ so với thời gian dự định. Tính quãng đường AB
Hướng dẫn:
Thời gian thực tế ô tô đi từ A đến B là:
3 giờ + 1 giờ = 4 (giờ)
Tỉ số thời gian của ô tô dự định đi và thực tế đi là:
\(3 : 4 = \dfrac {3}{4}\)
Trên cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau. Vì vậy, tỉ số vận tốc của ô tô dự định đi so với vận tốc thực tế ô tô đi là: \(\dfrac {4}{3}\)
Ta có sơ đồ sau:

Hiệu số phần bằng nhau là:
4 - 3 = 1 (phần)
=> Vận tốc thực tế ô tô đi là:
\(14 : 1 \times 3 = 42\) (km/giờ)
Quãng đường AB dài:
\(42 \times 4 = 168\) (km)
Đáp số: 168km
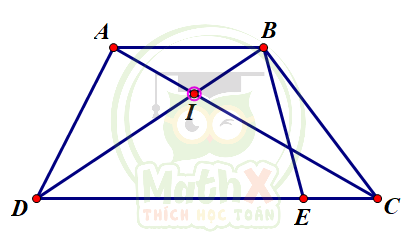
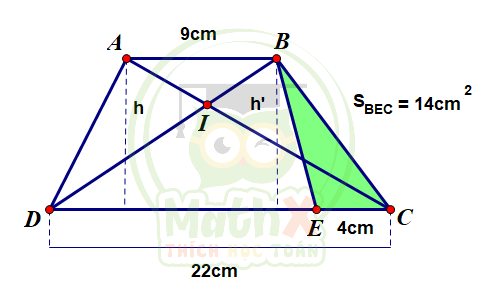
Bài 5: (3,0 điểm) Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Độ dài AB = 9cm, độ dài DC = 22cm. Trên cạnh DC lấy một điểm E sao cho CE = 4cm (hình vẽ), biết diện tích tam giác BEC là \(14 cm^2\)
a) So sánh diện tích hai tam giác AID và BIC.
b) Tính diện tích hình thang ABED.
c) Tìm tỉ số diện tích giữa tam giác ABD và tam giác BED.
Hướng dẫn:
Cách 1:
a) \(S_{ADC} = S_{BDC}\) (hai tam giác có chung đáy DC, có chiều cao hình thang ABCD)
Mà:
\(S_{ADC} = S_{AID} + S_{DIC}\)
\(S_{BDC} = S_{BIC} + S_{DIC}\)
Vậy: \(S_{ADI} = S_{BIC}\)
b) Chiều cao hình thang ABCD bằng chiều cao của hình tam giác BEC và bằng:
\(14 \times 2 : 4 = 7\) (cm)
Độ dài DE là:
22 - 4 = 18 (cm)
Diện tích hình thang ABED là:
\(S_{ABED} = (18+9) \times 7 : 2 = 94,5 \ (cm^2)\)
c) Ta có:
\(\dfrac {S_{ABD}}{S_{BED}} = \dfrac {AB \times h : 2}{DE \times h' : 2}\)
Mà h và h' đều là chiều cao của hình thang ABED:
\(\Rightarrow \dfrac {S_{ABD}}{S_{BED}} = \dfrac {AB \times h : 2}{DE \times h' : 2} = \dfrac {AB}{DE} = \dfrac {9}{18} = \dfrac {1}{2}\)
Câu c cách 2:
Diện tích tam giác ABD là:
\(S_{ABD} = 9 \times 7 : 2 = 31,5 \ (cm^2)\)
Diện tích tam giác BED là:
\(S_{BED} = 18 \times 7 : 2 = 63 \ (cm^2)\)
Tỉ số diện tích giữa tam giác ABD và tam giác BED là:
\(\dfrac {S_{ABD}}{S_{BED}} = \dfrac {31,5}{63} = \dfrac {1}{2}\)
Cách 2:
Chiều cao của tam giác BEC hạ từ B xuống cạnh EC:
\(14 \times 2 : 4 = 7\) (cm)
Các tam giác BCD, BDE, DAB, DAC và hình thang ABED đều có cùng chiều cao với tam giác BEC (hạ từ B xuống cạnh EC) và bằng 7cm
a) \(S_{ADC} = S_{BDC}\) (hai tam giác có chung đáy DC, có chiều cao bằng 7cm)
Mà:
\(S_{ADC} = S_{AID} + S_{DIC}\)
\(S_{BDC} = S_{BIC} + S_{DIC}\)
Vậy: \(S_{ADI} = S_{BIC}\)
b) Độ dài DE = 22 - 4 = 18 (cm)
Diện tích hình thang ABED là:
\(S_{ABED} = (18+9) \times 7 : 2 = 94,5 \ (cm^2)\)
c) \(\dfrac {S_{ABD}}{S_{BED}} = \dfrac {AB \times 7 : 2}{DE \times 7 : 2} = \dfrac {AB}{DE} = \dfrac {9}{18} = \dfrac {1}{2}\)
Đáp số:
a) \(S_{ADI} = S_{BIC}\)
b) \(S_{ABED} = 94,5 \ cm^2\)
c) \(\dfrac {S_{ABD}}{S_{BED}} = \dfrac {1}{2}\)
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Nguyễn Tri Phương - Thừa Thiên Huế năm học 2023 - 2024. Các em đọc kĩ đề bài, luyện tập tự làm trước khi xem đáp án, chúc các em ôn tập tốt và đạt điểm cao trong kì thi sắp tới.
Ngoài ra, các em học sinh và phụ huynh tham khảo thêm đề và hướng dẫn giải của một số trường chất lượng cao khác như Amsterdam hay Lương Thế Vinh tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS AMSTERDAM 2023-2024
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS LƯƠNG THẾ VINH 2023-2024
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS NGUYỄN TẤT THÀNH 2023-2024
GIẢI CHI TIẾT ĐỀ TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS NGÔI SAO 2023 2024 - MATHX