 Trường Toán Online MATHX
Trường Toán Online MATHX
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 10 năm học 2024 2025, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em bộ đề tuyển tập 50 câu hỏi trắc nghiệm để 01 làm online có đính kèm đáp án để giúp các em có thể tự luyện tập thêm tại nhà. Hy vọng rằng tài liệu này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới.
Hướng dẫn: Dưới đây là bộ đề câu hỏi trắc nghiệm. Các em đọc kĩ đề bài, làm bài ra giấy, chọn phương án đúng và nhấn trả lời. Nếu trả lời đúng sẽ hiển thị ra nút xem lời giải, nhấn vào nút đó sẽ hiển thị giải chi tiết bên dưới phần chọn đáp án. Trả lời sai các em sẽ cần chọn lại phương án khác. Chúc các em học tốt!!
Môn: Toán
Năm học: 2024 - 2025
Mã Đề: 01
Câu 1. Tìm điều kiện xác định của phương trình \({\sqrt{\left(x-4\right)^{2}}}+{\dfrac{x-4}{\sqrt{x^{2}-8x+16}}}=2x\)
| A. \(x \geq 4\) | B. \(x \in R\) | C. x < 4 | D. \(x \neq 4\) |
\({\sqrt{\left(x-4\right)^{2}}}+{\dfrac{x-4}{\sqrt{x^{2}-8x+16}}}=2x\) xác định khi:
\(x^{2}-8x+16\gt 0\Leftrightarrow\left(x-4\right)^{2}\gt 0\Leftrightarrow x\neq4\)
Câu 2. Tính giá trị của biểu thức
\(\left(\sqrt{\dfrac{49}{3}}-\sqrt{\dfrac{25}{3}}+\sqrt{3}\right).\sqrt{3}=\)
| A. \(\dfrac{5}{\sqrt{3}}\) | B. \(5\sqrt{3}\) | C. \(\dfrac{\sqrt{3}}{5}\) | D. 5 |
\(\left(\sqrt{\dfrac{49}{3}}-\sqrt{\dfrac{25}{3}}+\sqrt{3}\right).\sqrt{3}= \left(\dfrac{7}{\sqrt{3}}-\dfrac{5}{\sqrt{3}}+\sqrt{3}\right).\sqrt{3}=7-5+3=5\)
Câu 3. Tính giá trị của biểu thức \(C={\sqrt{3+2{\sqrt{2}}}}-{\sqrt{7+2{\sqrt{10}}}}\) là:
| A. \(1+ \sqrt{5}\) | B. \(1- \sqrt{5}\) | C. \(2\sqrt{2} (1+ \sqrt{5})\) | D. \(2\sqrt{2} (1- \sqrt{5})\) |
\(C={\sqrt{3+2{\sqrt{2}}}}-{\sqrt{7+2{\sqrt{10}}}} = \sqrt{\left({\sqrt{2}}+1\right)^{2}}-\sqrt{\left({\sqrt{5}}+{\sqrt{2}}\right)^{2}}=\sqrt{2}+1-\sqrt{5}-{\sqrt{2}}=1-{\sqrt{5}}\)
Câu 4. Cho \(A=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\left(\dfrac{1}{2\sqrt{x}}-\dfrac{\sqrt{x}}{2}\right)\) Tìm số các giá trị của x sao cho \(A=1-{\sqrt{x}}\)
| A. 0 | B. 1 | C. 2 | D. 3 |
\(A=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\left(\dfrac{1}{2\sqrt{x}}-\dfrac{\sqrt{x}}{2}\right) \\ ={\dfrac{\left({\sqrt{x}}-1\right)^{2}-\left({\sqrt{x}}+1\right)^{2}}{\left({\sqrt{x}}+1\right)\left({\sqrt{x}}-1\right)}}. \dfrac{1-x}{2{\sqrt{x}}} \\ ={\dfrac{\left({\sqrt{x}}-1-{\sqrt{x}}-1\right)\left({\sqrt{x}}-1+{\sqrt{x}}+1\right)}{-2{\sqrt{x}}}} \\ ={\dfrac{-2.{\sqrt{x}}}{-2{\sqrt{x}}}}=1\)
\(A=1-{\sqrt{x}}\Leftrightarrow1-{\sqrt{x}}=1\Leftrightarrow{\sqrt{x}}=0\Rightarrow x=0\) (tm)
Câu 5. Cho \(P={\dfrac{\sqrt{x}}{\sqrt{x}-1}}+{\dfrac{3}{\sqrt{x}+1}}-{\dfrac{6{\sqrt{x}}-4}{x-1}}\) . Tìm tất cả các giá trị của x sao cho \(P < \dfrac {1}{2}\)
| A. \(\left\{ \begin{align} & 0 < x \leq 9 \\ & x \neq 1 \\ \end{align} \right.\) | B. \(\left\{ \begin{align} & 0 < x < 9 \\ & x \neq 1 \\ \end{align} \right.\) | C. \(\left\{ \begin{align} & 0 \leq x < 9 \\ & x \neq 1 \\ \end{align} \right.\) | D. \(\left\{ \begin{align} & 0 \leq x \leq 9 \\ & x \neq 1 \\ \end{align} \right.\) |
\(P={\dfrac{\sqrt{x}}{\sqrt{x}-1}}+{\dfrac{3}{\sqrt{x}+1}}-{\dfrac{6{\sqrt{x}}-4}{x-1}}\) ( \(x \geq 0\) ; \(x \neq 1\) )
\(= \dfrac {{\sqrt{x}}{\Big(}{\sqrt{x}}+1{\Big)}+3{\Big(}{\sqrt{x}}-1{\Big)}-6{\sqrt{x}}+4}{\left({\sqrt{x}}+1\right)\left({\sqrt{x}}-1\right)} \\ = \dfrac {x+{\sqrt{x}}+3{\sqrt{x}}-3-6{\sqrt{x}}+4}{\left({\sqrt{x}}+1\right)\left({\sqrt{x}}-1\right)} \\ = \dfrac{{\sqrt{x}}-1}{{\sqrt{x}}+1}\)
\(P\lt \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\lt \dfrac{1}{2} \Leftrightarrow{\dfrac{{\sqrt{x}}-1}{{\sqrt{x}}+1}}-{\dfrac{1}{2}}\lt 0\Leftrightarrow{\dfrac{2{\sqrt{x}}-2-{\sqrt{x}}-1}{2\left({\sqrt{x}}+1\right)}}\lt 0 \\ \Rightarrow{\sqrt{x}}-3\lt 0\Rightarrow{\sqrt{x}}\lt 3\Rightarrow x\lt 9 \\ \Rightarrow \left\{ \begin{align} & 0 \leq x < 9 \\ & x \neq 1 \\ \end{align} \right.\)
Câu 6. Cho hàm số bậc nhất có đồ thị là đường số d.Tìm hàm số đó biết d đi qua A(1;3), B(2;-1)
| A. y = -4x + 2 | B. y = -2x + 3 | C. y = -4x + 5 | D. y = -4x + 7 |
Goi hàm số cần tìm có dạng (d): y = ax + b ( \(a \neq 0\) )
Vì (d) đi qua A(1;3), B(2;-1) => \(\left\{ \begin{align} & a + b = 3 \\ & 2a + b = -1 \\ \end{align} \right. \Leftrightarrow \) \(\left\{ \begin{align} & a = -4 \\ & b = 7 \\ \end{align} \right.\)
Vậy hàm số cần tìm là y = -4x + 7
Câu 7. Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biieets d đi qua C(3;-2) và song song với \(\Delta:3x-2y+1=0\)
| A. \(y={\dfrac{1}{2}}x-{\dfrac{3}{2}}\) | B. \(y={\dfrac{3}{2}}x-{\dfrac{13}{2}}\) | C. \(y={\dfrac{3}{2}}x-{\dfrac{3}{2}}\) | D. \(y={\dfrac{3}{2}}x+{\dfrac{3}{2}}\) |
Gọi (d): y = ax + b (\(a \neq 0\) ) là đồ thị cần tìm
Vì \((d)// \Delta : \ 3x-2y+1=0\Rightarrow\) \(\left\{ \begin{align} & a = \dfrac {3}{2} \\ & b \neq \dfrac {1}{2} \\ \end{align} \right.\)
Để \((d)\!:y\!=\!{\dfrac{3}{2}}x\!+\!b\) đi qua (3;-2) => \(\left\{ \begin{align} & x = 3 \\ & y = -2 \\ \end{align} \right.\)
\(\Rightarrow-2={\dfrac{3}{2}}.3+b\Rightarrow b=-{\dfrac{13}{2}}\) (tm)
Vậy \((d) : y=\dfrac{3}{2}x-\dfrac{13}{2}\)
Câu 8. Cho hàm số bậc nhất có đồ thị là đường thẳng d.Tìm hàm số đó biết d đi
qua M(1;2) và cắt tia Ox, Oy tại P, Q sao cho \(S_{\Delta OPQ}\) nhỏ nhất
| A. y = 3x - 1 | B. y = -2x + 3 | C. y = -2x + 4 | D. y = 2x |
y = ax + b => 2 = a + b => b = 2 - a
Vì d cắt tia Ox, Oy
=> \(d\cap O x=P{\biggl(}-{\dfrac{b}{a}};0{\biggr)} , d \cap O y=Q{\big(}0;b,{\big)},b\gt 0\Rightarrow a\lt 0\)
\(S_{\Delta OPQ}\) min \(\Leftrightarrow \dfrac{1}{2}O P.O Q_{\mathrm{min}} \Leftrightarrow{\dfrac{1}{2}}{\bigg|} \dfrac {b}{a} {\bigg|} {\bigg|}b{\bigg|}_{\operatorname*{min}} \Leftrightarrow \dfrac {b^2}{a}min\)
\(\Leftrightarrow{\dfrac{\left(2-a\right)^{2}}{a}}={\dfrac{4}{a}}-4+a\operatorname*{min}_{a}\geq2{\sqrt{{\dfrac{4}{a}}}}\,a-4=0\)
Dấu " = " xảy ra khi \(a = \dfrac {4}{a} \Leftrightarrow a=-2(d o\ a\lt 0)\Leftrightarrow b=4\)
Vậy y = -2x + 4
Câu 9. Cho hàm số bậc nhất có đồ thị là đường thẳng d.Tìm hàm số đó biết d đi qua N (2;-1) và \(d\perp d'\) với d': y = 4x + 3
| A. \(y=-\dfrac {1}{4}x -\dfrac {1}{2}\) | B. \(y=-\dfrac {1}{4}x -\dfrac {1}{3}\) | C. \(y=\dfrac {1}{4}x +\dfrac {1}{2}\) | D. \(y=\dfrac {1}{4}x -\dfrac {3}{2}\) |
Hàm số \(\left(d\right):y=a x+b{\big(}a\neq0{\big)}\perp d^{'}\!:y=4x+3\Rightarrow a.4=-1\Rightarrow a=-{\dfrac{1}{4}}\)
Đồ thị hàm số \(y=-\dfrac {1}{4}x +b\) qua điểm N(2;-1) => \(-1={\dfrac{-1}{4}}.2+b\Leftrightarrow b=-{\dfrac{1}{2}}\)
Vậy \(y=-\dfrac {1}{4}x -\dfrac {1}{2}\)
Câu 10. Cho đường thẳng \(d:y=(m-1)x+m\) và \(d' :y=\left(m^{2}-1\right)x+1\) . Tìm tất cả các giá trị của m để hai đường thẳng d, d' song song với nhau
| A. m = 0, m = 1 | B. m = 2 | C. m = 0 | D. m = 1 |
Để các đường thẳng \(d:y=(m-1)x+m\) và \(d' :y=\left(m^{2}-1\right)x+1\) song song với nhau thì
\(\left\{ \begin{align} & m - 1 = m^2 - 1 \\ & m \neq 1 \\ \end{align} \right.\) \(\Leftrightarrow \left\{ \begin{align} & m^2 - m = 0 \\ & m \neq 1 \\ \end{align} \right.\) \(\Leftrightarrow \left\{ \begin{align} & \left[\begin{array}{c}{{m=0}}\\ {{m=1 \Rightarrow m=0}}\end{array}\right. \\ & m \neq 1 \\ \end{align} \right.\)
Câu 11. Tìm phương trình đường thẳng d: y = ax + b. Biết đường thẳng d đi qua điểm I(2;3) và tạo với hai tia Ox, Oy một tam giác vuông cân
| A. y = x + 5 | B. y = -x + 5 | C. y = -x - 5 | D. y = x - 5 |
d: y = ax + b đi qua điểm I(2;3) => 3 = 2a + b (*)
Ta có: \(d\cap O x=d\left(-{\dfrac{b}{a}};0\right),d\cap O y=B\left(0;b\right)\)
\(\Rightarrow O A=\left|-{\dfrac{b}{a}}\right|={\dfrac{b}{a}},O B=\left|b\right|=b\) (do A, B thuộc tia Ox, Oy)
Tam giác OAB vuông tại O. Do đó, Tam giác OAB vuông cân khi OA = OB
\(\Rightarrow-{\dfrac{b}{a}}=b\Rightarrow\) \(\left[\begin{array}{c} {{b=0 \Rightarrow A=B=O (0;0) (ktm)}} \\ {{a=-1 \Rightarrow \begin{cases} 3=2a+b \\ a=-1 \end{cases} \Rightarrow \begin{cases} a=-1 \\ b=5 \end{cases} }}\end{array}\right.\)
Vậy đường thẳng cần tìm là: y = -x + 5
Câu 12. Cho hàm số y = ax + b có đồ thị là hình dưới. Tìm a b
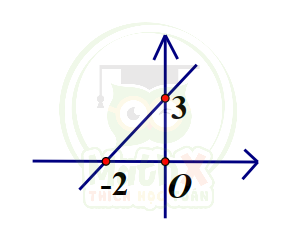
| A. a = -2, b = 3 | B. \(a = -\dfrac {3}{2}, b=2\) | C. a = -3, b = 3 | D. \(a = \dfrac {3}{2}, b=3\) |
Đồ thị hàm số y = ax + b đi qua điểm (-2;0), (0;3)
\(\Rightarrow \begin{cases} -2a+b=0 \\ b=3 \end{cases} \Rightarrow \begin{cases} a=\dfrac{3}{2} \\ b=3 \end{cases}\)
Câu 13. Đồ thị hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A B C D , , , dưới đây. Hỏi hàm số đó là hàm số nào ?
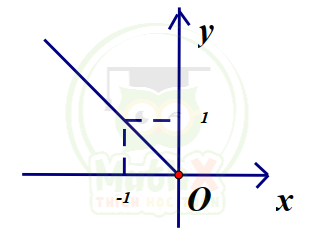
| A. y = |x| | B. y = -x | C. y = |x| với x > 0 | D. y = -x với x < 0 |
Vì y = ax đi qua (-1;1) => a = -1 và nằm về phía x < 0
Câu 14. Khẳng định nào về hàm số y = 3x + 5 là sai
A. Đồng biến trên R
B. Cắt Ox tại \(\left(-{\dfrac{5}{3}};0\right)\)
C. Cắt Oy tại (0;5)
D. Nghịch biến trên R
Vì y = 3x + 5 có a = 3 > 0 nên đồng biến trên R
Câu 15. Tập xác định của hàm số \(y={\sqrt{\left|x-2\right|}}\) là:
| A. R | B. \(\left[\begin{array}{c} {{m>2}} \\ {{m<2}}\end{array}\right.\) | C. \(m \leq 2\) | D. \(m \geq 2\) |
\(y={\sqrt{\left|x-2\right|}}\) xác định khi |x - 2| > 0 => \(\left[\begin{array}{c} {{x-2\geq0}} \\ {{x-2<0}}\end{array}\right.\) \(\Leftrightarrow \left[\begin{array}{c} {{x\geq2}} \\ {{x-<2}}\end{array}\right.\) => \(x \in R\)
Câu 16. Với giá trị nào của m thì tham số y = (2-m)x + 5m nghịch biến trên R
| A. m > 2 | B. m < 2 | C. m = 2 | D. \(m \neq 2\) |
Hàm số y = (2-m)x + 5m nghịch biến khi 2 - m < 0 => m > 2
Câu 17. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
| A. \(2x+3y^2=0\) | B. \(xy-x=1\) | C. \(x^3+y=5\) | D. \(2x-3y=4\) |
Phương trình bậc nhất hai ẩn có dạng ax + by = c
Câu 18. Tìm nghiệm của hệ phương trình \(\begin{cases} 4x-5y=2 \\ 3y+x=1 \end{cases}\)
| A. \(\left(-{\dfrac{7}{19}};{\dfrac{2}{19}}\right)\) | B. \(\left({\dfrac{11}{17}};{\dfrac{2}{17}}\right)\) | C. \(\left({\dfrac{7}{19}};{\dfrac{2}{19}}\right)\) | D. \(\left(-{\dfrac{11}{17}};{\dfrac{2}{17}}\right)\) |
\(\begin{cases} 4x-5y=2 \\ 3y+x=1 \end{cases} \Leftrightarrow \begin{cases} 12x-15y=6 \\ 5x+15y=5 \end{cases} \\ \Leftrightarrow \begin{cases} 17x=11 \\ y=\dfrac{1-x}{3} \end{cases} \Leftrightarrow \begin{cases} x=\dfrac{11}{17} \\ y=\dfrac{2}{17} \end{cases}\)
Câu 19. Tháng thứ nhất, hai tổ sản xuất được 1000 chi tiết máy. Tháng thứ hai tổ I vượt mức 20%và tổ II vượt mức 15% so với tháng thứ nhất. Vì vậy hai tổ sản xuất được 1170chi tiết máy. Hỏi tháng thứ hai, mỗi tổ sản xuất được bao nhiêu chi tiết máy ?
A. Tổ I: 480 chi tiết máy, tổ II: 690 chi tiết máy
B. Tổ I: 450 chi tiết máy, tổ II: 720 chi tiết máy
C. Tổ I: 400 chi tiết máy, tổ II: 600 chi tiết máy
D. Tổ I: 600 chi tiết máy, tổ II: 570 chi tiết máy
Gọi x y , là số chi tiết máy hai tổ tháng thứ nhất làm được \(\left(x,y\in\mathbb{N}^{*};x,y\lt 1000\right)\)
Theo bài ta có hệ phương trình: \( \begin{cases} x+y=1000 \\ 1,2x+1,15y=1170 \end{cases} \Leftrightarrow \begin{cases} x=400 \\ y=600 \end{cases} (tm)\)
Vậy tháng thứ hai, Tổ I: 400 . 1,2 = 480 (chi tiết máy), tổ II: 600.1,15 = 690 (chi tiết máy)
Câu 20. Cho hệ phương trình \(\begin{cases} x-y+m=0 \\ (x+y-2)(x-2y+1)=0 \end{cases}\) . Tìm tất cả các giá trị của m để hệ phương trình trên có nghiệm duy nhất ?
| A. m = 0 | B. m = 1 | C. m = 2 | D. m = 3 |
\(\begin{cases} x-y+m=0 \ \ (1) \\ (x+y-2)(x-2y+1)=0 \ \ (2) \end{cases}\)
Từ (1) => x = y - m thay vào (2) ta có:
\((y-m+y-2)\bigl(y-m-2y+1\bigr)=0\Leftrightarrow(2y-m-2)\bigl(-y-m+1\bigr)=0\)
\(\Leftrightarrow \left[\begin{array}{c} {{2y-m-2=0}} \\ {{-y-m+1=0 }}\end{array}\right. \Leftrightarrow \left[\begin{array}{c} {{y=\dfrac{m+2}{2}}} \\ {{y=1-m }}\end{array}\right. \)
Để hệ phương trình có nghiệm duy nhất thì \({\dfrac{m+2}{2}}=1\!-\!m\Leftrightarrow m\!+\!2=\!2\!-\!m\Leftrightarrow m\!=\!0\)
Câu 21. Cho ba đường thẳng \(y=3x-2, \ y=-{\dfrac{1}{3}}x+{\dfrac{4}{3}}, \ y=-2x+8\) .Miền được tạo bởi đồ thị của ba đường thẳng đã cho là tam giác gì ?
A. Tam giác thường
B. Tam giác vuông cân
C. Tam giác cân
D. Tam giác vuông
Ta gọi A B C , , là giao điểm của 2 đường thẳng đôi một của 3 dường thẳng trên
\(\Leftrightarrow A{\big(}1;1{\big)},B{\big(}4;0{\big)},C{\big(}2;4{\big)}\Rightarrow AB={\sqrt{10}}, AC={\sqrt{10}},B C={\sqrt{20}}\)
\(\Rightarrow A B=A C ; B C^{2}=A B^{2}+AC^{2}\)
Nên \(\Delta ABC\) vuông cân tại A
Câu 22. Với những giá trị của m để phương trình \(x^{2}-m x+m-2=0\) có hai nghiệm phân biệt \(x_{1},x_{2}\) . Khi đó tính \(A=x_{1}^{2}+x_{2}^{2}\)
| A. \(A = m^2\) | B. \(A = m^2 + m -2\) | C. \(A = m^2 + 2m - 4 \) | D. \(A = m^2 - 2m + 4 \) |
\(x^{2}-m x+m-2=0\) có \(\Delta=m^{2}-4\bigl(m-2\bigr)=m^{2}-4m+8\gt 0\) nên phương trình luôn có hai nghiệm.
Áp dụng hệ thức Vi-et: \(\begin{cases} x_{1}+x_{2}=m \\ x_{1}x_{2}=m - 2 \end{cases}\)
\(\Rightarrow A=x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2x_{1}x_{2}=m^{2}-2\left(m-2\right)=m^{2}-2m+4\)
Câu 23. Với những giá trị của m để phương trình \(x^{2}-m x+m-2=0\) có hai nghiệm \(x_{1},x_{2}\) thỏa mãn \({\dfrac{x_{1}^{2}-2}{x_{1}-1}}.{\dfrac{x_{2}^{2}-2}{x_{2}-1}}=4\) . Khi đó m là nghiệm của phương trình nào dưới đây
| A. \(m^2 + 2m + 1 = 0\) | B. \(2m^2 - 5m + 3 = 0\) | C. \(m^2 - 3m + 2 = 0 \) | D. \(m^2 - 4 = 0\) |
\(x^{2}-m x+m-2=0\) có \(\Delta=m^{2}-4\bigl(m-2\bigr)=m^{2}-4m+8\gt 0\) nên phương trình luôn có hai nghiệm phân biệt: \(\begin{cases} x_{1}+x_{2}=m \\ x_{1}x_{2}=m - 2 \end{cases}\)
Ta có:
\({\dfrac{x_{1}^{2}-2}{x_{1}-1}}.{\dfrac{x_{2}^{2}-2}{x_{2}-1}}=4\Leftrightarrow{\dfrac{x_{1}^{2}x_{2}^{2}-2\Bigl(x_{1}^{2}+x_{2}^{2}\Bigr)+4}{x_{1}x_{2}-\bigl(x_{1}+x_{2}\bigr)+1}}=4\)
\(\Leftrightarrow{\dfrac{\left(x_{1}x_{2}\right)^{2}-2\left[\left(x_{1}+x_{2}\right)^{2}-2x_{1}x_{2}\right]+4}{x_{1}x_{2}-\left(x_{1}+x_{2}\right)+1}}=4\)
\(\Leftrightarrow{\dfrac{\left(m-2\right)^{2}+2\left(m^{2}-2m+4\right)+4}{m-2+m+1}}=4\)
\(\Rightarrow 3m^{2}-8m+16=8m-4\Longleftrightarrow3m^{2}-16m+20=0\)
\(\Leftrightarrow \left[\begin{array}{c} {{m=\dfrac{10}{3}}} \\ {{m=2}}\end{array}\right.\)
\(m={\dfrac{10}{3}};m=2\) là nghiệm của phương trình \(m^2 - 3m + 2\)
Câu 24. Cho phương trình \(m x^{2}-2x+4=0\) (m :tham số, x :ẩn số). Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt ?
| A. \(m < \dfrac{1}{4}\) | B. \(m < \dfrac{1}{4}, \ m \neq 0\) | C. \(m > \dfrac{1}{4}\) | D. \(m \in R\) |
Phương trình \(m x^{2}-2x+4=0\) ( m :tham số, x :ẩn số) là hàm số bậc hai khi m ≠ 0
Phương trình có hai nghiệm phân biệt khi
\(\Delta^{\prime}\gt 0\Leftrightarrow1-4m\gt 0\Leftrightarrow m\lt \dfrac{1}{4} và \ m\neq0\)
Câu 25. Phương trình bậc hai nào sau đây có nghiệm \({\sqrt{3}}+{\sqrt{2}}\) và \({\sqrt{3}}-{\sqrt{2}}\)
A. \(x^{2}+2{\sqrt{3}}x+1=0\)
B. \(x^{2}-2{\sqrt{3}}x+1=0\)
C. \(x^{2}+2{\sqrt{3}}x-1=0\)
D. \(x^{2}-2{\sqrt{3}}x-1=0\)
Áp dụng hệ thức Vi et khi ta có hai nghiệm
Nên: \(\begin{cases} x_{1}+x_{2}=2{\sqrt{3}} \\ x_{1}x_{2}=-1 \end{cases}\)
Ta thấy phương trình \(x^{2}-2{\sqrt{3}}x-1=0\) thỏa mãn
Câu 26. Đường thẳng \(\left(d\right)\!:y=-x+6\) và parabol \(\left(P\right)\!:y=x^{2}\)
A. Tiếp xúc nhau
B. Cắt nhau tại hai điểm A(-3;9), B(2;4)
C. Không cắt nhau
D. Cắt nhau tai hai điểm A, B và AB = 56
Ta có phương trình hoành độ giao điểm: \(x^2+x-6=0\)
\(\Leftrightarrow \left[\begin{array}{c} {{x=2 \Rightarrow y=4}} \\ {{x=-3 \Rightarrow y=9}}\end{array}\right. \)
Câu 27. Hàm số \(y=\left({m-\dfrac{1}{2}}\right)x^{2}\) đồng biến với x < 0 nếu:
| A. \(m < \dfrac {1}{2}\) | B. m = 1 | C. \(m > \dfrac {1}{2}\) | D. \(m = \dfrac {1}{2}\) |
Hàm số \(y=\left({m-\dfrac{1}{2}}\right)x^{2}\) đồng biến khi \(x\lt 0\Leftrightarrow m-{\dfrac{1}{2}}\lt 0\Leftrightarrow m\lt {\dfrac{1}{2}}\)
Câu 28. Parabol \(\left(P\right):y=\left(m-{\dfrac{1}{2}}\right)x^{2}\) có đồ thị trong hình dưới có m bằng bao nhiêu
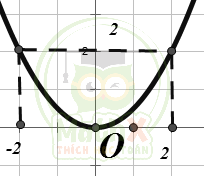
| A. 1 | B. -1 | C. 2 | D. \(\dfrac {1}{2}\) |
\(\left(P\right):y=\left(m-{\dfrac{1}{2}}\right)x^{2}\) đi qua điểm \(\left(2;2\right)\Rightarrow m-{\dfrac{1}{2}}={\dfrac{2}{2^2}}\Leftrightarrow m=1\)
Câu 29. Parabol \(\left(P\right):y=\left(m-{\dfrac{1}{2}}\right)x^{2}\) có đồ thị là hình nào dưới đây ?
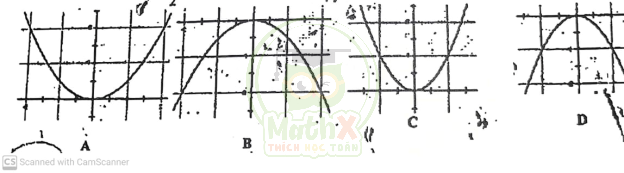
Chọn đáp án B
Câu 30. Một vận động viên nhảy cầu trong hồ nước. Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức \(h=-(x-1)^2+4\) . Khi vận động viên cách mặt nước 3m, tính khoảng cách x
| A. x = 0 | B. x = 2 | C. \(\Leftrightarrow \left[\begin{array}{c} {{x=0}} \\ {{x=2}}\end{array}\right.\) | D. x = 3 |
Khi ở độ cao 3m
=> \(h=-(x-1)^2+4=3 \Leftrightarrow(x-1)^{2}=1 \Leftrightarrow \left[\begin{array}{c} {{x-1=1}} \\ {{x-1=-1}}\end{array}\right.\Leftrightarrow \left[\begin{array}{c} {{x=0}} \\ {{x=2}}\end{array}\right.\)
Vì x là khoảng cách từ điểm rơi đến chân cầu nên x > 0 => x = 2
Câu 31. Tìm tập nghiệm của phương trình \({\sqrt{x^{2}-6x+9}}=2x+1\)
| A. \(S=\left\{-4;{\dfrac{2}{3}}\right\}\) | B. \(S=\left\{-4\right\}\) | C. \(S=\left\{{\dfrac{2}{3}}\right\}\) | D. \(S= \emptyset\) |
\({\sqrt{x^{2}-6x+9}}=2x+1 {\biggl(}x\geq-{\dfrac{1}{2}}{\biggr)}\Rightarrow x^{2}-6x+9=4x^{2}+4x+1\)
\(\Leftrightarrow3x^{2}+10x-8=0\Leftrightarrow\) \(\Leftrightarrow \left[\begin{array}{c} {{x=\dfrac {2}{3} \ (tm)}} \\ {{x=-4 \ (ktm) }}\end{array}\right.\)
Câu 32. Tìm tất cả các giá trị của tham số m để phương trình \(x^4 + 4x^2 - m + 4 = 0\) có bốn nghiệm phân biệt ?
| A. \(m \geq -3\) | B. \(m \geq 3\) | C. m = 3 | D. \(m \in \emptyset\) |
\(x^4 + 4x^2 - m + 4 = 0\) (1)
Đặt \(t = x^2\) => phương trình thành \(t^{2}+4t-m+4 \ \ (2)\)
Để phương trình (1) có 4 nghiệm phân biệt thì pt (2) có 2 nghiệm dương phân biệt
=> \(\begin{cases} S>0 \\ P>0 \end{cases} \Leftrightarrow \begin{cases} -4>0 \\ -m+4>0 \end{cases} \Leftrightarrow \) vô lý. Vậy không tìm được giá trị m
Câu 33. Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, \(\widehat {ADC} = 40^o\), \(\widehat {ABC} = 90^o\) Hãy tính chiều dài cạnh AD và diện tích của chiếc diều (làm tròn đến hàng phần nghìn)
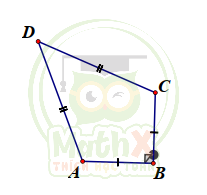
A. \(AD \approx 24,811cm; S_{A B C D}\approx269,849 {cm}^{2}\)
B. \(AD \approx 24,812cm; S_{A B C D}\approx269,850 {cm}^{2}\)
C. \(AD \approx 24,81cm; S_{A B C D}\approx269,85 {cm}^{2}\)
D. \(AD \approx 24,813cm; S_{A B C D}\approx269,850 {cm}^{2}\)
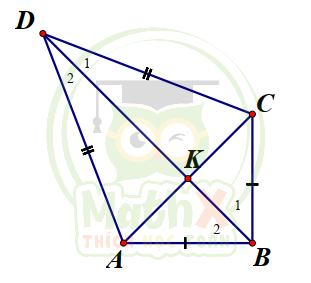
\(\Delta A B D=\Delta C B D \ \ (c.c.c)\Rightarrow \widehat {d_1} = \widehat {d_2} = \dfrac {40^o}{2}=20^o \ , \widehat {b_1} + \widehat {b_2} = 90^o\)
Mặt khác: AD = CD , AB = CB
=> BD là đường trung trực của AC
=> \(\begin{cases} \widehat K = 90^o \\ AK=CK \end{cases}\)
\(A K=A B.\sin B=6{\sqrt{2}}{\big(}c m{\big)}\Rightarrow A D={\dfrac{A K}{\sin D_{2}}}\approx24.81(c m{\big)}\)
\(D K=AK.\cot \widehat {D_{2}} \approx23,3c m\Rightarrow S_{\Delta ADK} \approx98,9\left(c m^{2}\right)\)
\(\Rightarrow S_{A B C D}=2.S_{A D K}+S_{A B C}\approx269,85(c m^{2})\)
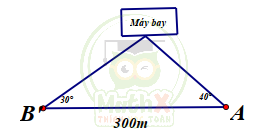
Câu 34. Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là \(40^o\) và tại vị trí B là \(30^o\). Hãy tính độ cao của máy bay .
| A.102,00m | B. 102,07m | C. 102,60m | D.102,06m |
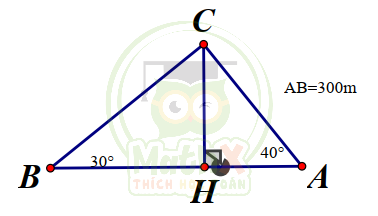
Độ cao của máy bay: CH
Xét \(\Delta C H B:C H=B H.{\mathrm{tan}}B=B H.{\mathrm{tan}}30^{\circ}={\dfrac{B H}{\sqrt{3}}}\Rightarrow B H=C H.{\sqrt{3}}\)
Xét \(\Delta A H C:C H=AH.\tan A=A H.\tan40^{\circ}\Rightarrow AH=\dfrac{C H}{\tan40^{\circ}}\)
\(AB=AH+B H=C H{\sqrt{3}}+{\dfrac{C H}{\tan{40^{\circ}}}}\)
\(AB=300=\left({\sqrt{3}}+{\frac{1}{\tan{40^{\circ}}}}\right)C H\Rightarrow C H={\dfrac{300}{{\sqrt{3}}+{\dfrac{1}{\tan{40^{\circ}}}}}}\approx102{,}61(m)\)
Câu 35. Cho tam giác ABC có AB = 10cm, AC = 12cm, \(\widehat A = 40^o\). Góc C gần bằng góc nào nhất ?
| A. \(50^o\) | B. \(60^o\) | C. \(70^o\) | D. \(56^o\) |
Hạ \(B H\perp A C\). Áp dụng tỉ số lượng giác của góc nhọn trong các tam giác vuông:
\(AH=10.{\mathrm{cos}}40^{\circ}\approx7.66;B H=10.{\mathrm{sin}}40^{\circ}\approx6.43\)
\(\Rightarrow HC=AC-AH=12-7.66=4.34\)
\(\Rightarrow\tan C={\dfrac{B H}{H C}}={\dfrac{6.43}{4.34}}\Rightarrow \widehat C\approx56^{\circ}\)
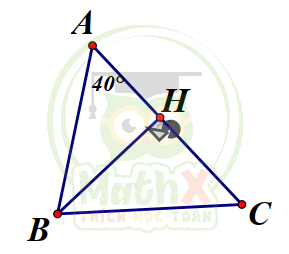
Câu 36. Cho tam giác ABC có trực tâm H là trung điểm của đường cao AD .Đẳng thức nào sau đây đúng ?
A. \(\cos B=\cos B.\cos C\)
B. \(\cos A=\cos A.\cos C\)
C. \(\cos A=\cos B.\cos C\)
D. \(\cos A=\cos B.\cos B\)
Đường cao \(B E,C F,\widehat {D H C}=90^{\circ}-\widehat {D C H}=\widehat {A B C}\)
\(\Rightarrow H D=H C\cdot\cos \widehat {D H C}=H C.\cos B\)
\(AH= HE:\cos\widehat{AH E}=H E:\cos\widehat C={\dfrac{H C.\cos\widehat {EHC}}{\cos \widehat C}}={\dfrac{H C.\cos\widehat A}{\cos\widehat C}}\)
\(AH=DH\Rightarrow\cos B.\cos C=\cos A\)
Câu 37. Cho tam giác ABC vuông tại A.Đẳng thức nào sau đây đúng ?
A. \(\tan{\dfrac{\angle A B C}{2}}={\dfrac{A C}{A C+B C}}\)
B. \(\tan{\dfrac{\angle A B C}{2}}={\dfrac{A C}{A B-B C}}\)
C. \(\tan{\dfrac{\angle A B C}{2}}={\dfrac{A C}{A B+B C}}\)
D. \(\tan{\dfrac{\angle A B C}{2}}={\dfrac{A C}{A B.B C}}\)
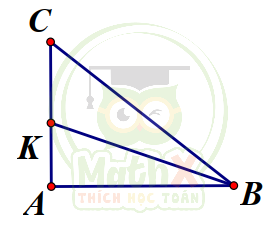
Kẻ BK là tia phân giác của \(\angle ABC \ (K\in{A C})\). Theo tính chất của tia phân giác
\(\Rightarrow{\dfrac{A K}{A B}}={\dfrac{K C}{B C}}\)
Áp dụng tính chất của tỉ lệ thức ta có :
\({\dfrac{A K}{A B}}={\dfrac{K C}{B C}}={\dfrac{A K+K C}{A B+BC}}={\dfrac{A C}{A B+B C}}\)
Mà \(\tan\angle A B K={\dfrac{A K}{A B}}={\dfrac{A C}{A B+B C}}\)
Câu 38. Cho \(\Delta ABC\), một đường thẳng song song với cạnh BC cắt cạnh AB và cạnh AC lần lượt tại D và F. Khẳng định nào sau đây là đúng ?
| A. \(\dfrac {AD}{FB} = \dfrac {AF}{AC}\) | B. \(\dfrac {AD}{FD} = \dfrac {AF}{CF}\) | C. \(\dfrac {AB}{AD} = \dfrac {BC}{DF}\) | D. \(\dfrac {AB}{AD} = \dfrac {AF}{AC}\) |
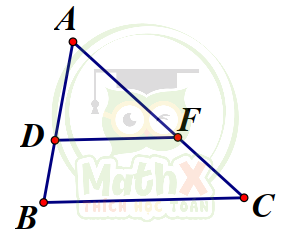
Áp dụng định lý Ta let ta có :
\(\dfrac {AB}{AD} = \dfrac {BC}{DF}\)
Câu 39. \(\Delta ABC\) đồng dạng với \(\Delta DEF\) theo tỉ số đồng dạng \(k_1\) , \(\Delta DEF\) đồng dạng với \(\Delta GHK\) theo tỉ số đồng dạng \(k_2\) . \(\Delta ABC\) đồng dạng với \(\Delta GHK\) theo tỉ số :
| A. \(\dfrac {k_1}{k_2}\) | B. \(k_1+k_2\) | C. \(k_1-k_2\) | D. \(k_1.k_2\) |
\(\Delta ABC\) đồng dạng với \(\Delta GHK\) theo tỉ số : \(k_1.k_2\)
Câu 40. Trên đường tròn (O) lấy ba cung liên tiếp \({\widehat{A B}}={\widehat{B C}}={\widehat{C D}}\) sao cho số đo của chúng đều bằng \(50^o\). Gọi I là giao điểm của hai tia AB, DC; H là giao điểm của hai dây AC, BD. Khẳng định nào sau đây sai ?
A. \(\angle A H D=130^{\circ}\)
B. \(\angle A I C =80^{\circ}\)
C. \(\Delta IAD\) là tam giác cân
D. \(\angle A C B =50^{\circ}\)
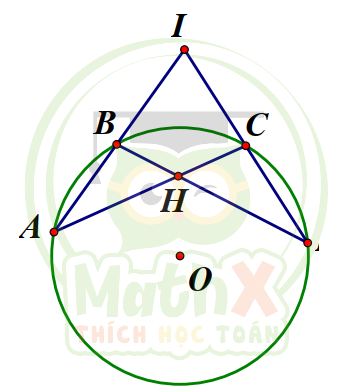
\(\angle A C B={\dfrac{1}{2}}s d{\widetilde{A B}}={\dfrac{1}{2}}.50^{\circ}=25^{\circ}\) nên câu D sai
Câu 41. Cho nửa đường tròn tâm O, đường kính AB, C là điểm tùy ý trên nửa đường tròn. Tiếp tuyến của (O) tại A cắt tia BC tại D. Tia phân giác của góc ∠BAC cắt dây BC tại M và cung BC tại N. Tam giác DAM là tam giác gì ?
A. Tam giác vuông
B. Tam giác vuông cân
C. Tam giác cân nhưng không đều
D. Tam giác đều
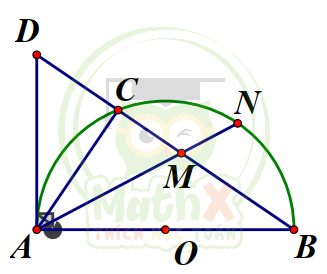
Ta có AD là tiếp tuyến nên
\(\angle D A M={\dfrac{1}{2}}\,s d{\widehat{{A N}}}={\dfrac{1}{2}}{\Bigl(}\,s d\,{\widehat{{A C}}}+s d{\widehat{{C N}}}{\Bigr)} \ \ (1)\)
\(\angle D M A\) là góc có đỉnh trong đường tròn nên:
\(\angle D M A={\dfrac{1}{2}}\biggl(s d \widehat {AC}+s d{\widehat {NB}} \biggr) \ \ (2)\)
Mà AN là tia phân giác
\(\Rightarrow s d \widehat {CN} = s d{\widehat {NB}} \ \ (3)\)
Từ (1) (2) (3) => \(\angle DAM=\angle DMA \Rightarrow \Delta DAM\) cân nhưng không đều
Câu 42. Cho tam giác ABC có góc A bằng \(80^o\) nội tiếp đường tròn (O), kéo dài BA một đoạn AD = AC.Cho BC cố định, A di động trên cung chứa góc \(80^o\) thuộc (O) thì D di động trên đường nào ?
A. Đường tròn tâm C, bán kính CD
B. Cung chứa góc \(50^o\) vẽ trên BC cùng phía với cung BAC
C. Hai cung chứa góc \(50^o\) vẽ trên BC và đối xứng nhau qua BC
D. Đường tròn đường kính BC
Ta có: \(AD = AC \Rightarrow \Delta ACD \) cân tại A
\(\Rightarrow\angle AD C={\dfrac{180^{\circ} - \angle D A C}{2}}={\dfrac{180^{\circ}-80^{\circ}}{2}}=50^{\circ}\Rightarrow\angle B D C=50^{\circ}\)
Mà BC cố định nên điểm D thuộc cung chứa góc 50° dựng trên BC
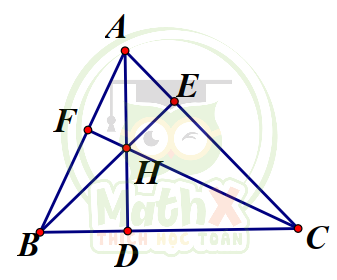
Câu 43. Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD, tia AH cắt BC tại F. Số tứ giác nội tiếp được đường tròn có trong hình vẽ là
| A. 4 tứ giác | B. 6 tứ giác | C. 7 tứ giác | D. 8 tứ giác |
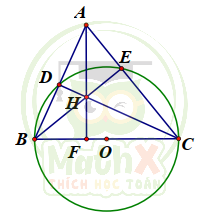
Các tứ giác nội tiếp : BDEC. ADHE, BDFH, FHEC
=> Có 4 tứ giác nội tiếp
Câu 44. Cho tam giác ABC vuông tại A, đường cao AH nội tiếp đường tròn (O; R). Gọi I, K theo thứ tự là điểm đối xứng của H qua hai cạnh AB, AC. Khẳng định nào sau đây đúng?
A. Tứ giác AHBI nội tiếp đường tròn đường kính AB
B. Tứ giác AHCK nội tiếp đường tròn đường kính AC
C. Ba điểm I, A, K thẳng hàng
D. Cả ba đáp án trên đều đúng
Cả 3 ý đều đúng
Câu 45. Cho hai đường tròn (O; 8cm) và (O; 5cm) . Hai bán kính OM, ON của đường tròn lớn cắt đường tròn nhỏ tại E, F. Cho biết góc \(∠MON = 100 ^o\) .Tính diện tích hình vành khăn nằm trong góc ∠MON (hình giới hạn bởi hai đường tròn) (làm tròn kết quả đến chữ số thập phân thứ nhất)
| A. \(122,5cm^2\) | B. \(34cm^2\) | C. \(34,2cm^2\) | D. \(122,6cm^2\) |
Diện tích hình vành khăn:
\(S_{vanh \ khan}=\pi R^{2}-\pi R'^{2}=\pi\left(8^{2}-5^{2}\right)\approx122,5(c m^{2})\)
Câu 46. Cho đường tròn (O; R) vẽ hai bán kính OA, OB vuông góc với nhau, tiếp tuyến của (O) tại A và B cắt nhau tại T. Tính theo R diện tích hình giới hạn bởi hai tiếp tuyến TA, TB và cung nhỏ AB
| A. \({\dfrac{R^{2}}{4}}(4-\pi)\) | B. \({\dfrac{R^{2}}{4}}(\pi-3)\) | C. \({\dfrac{R^{2}}{4}}(\pi+1)\) | D. \({\dfrac{R^{2}}{4}}(4+\pi)\) |
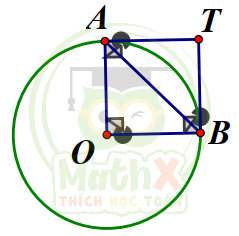
Ta có: \(\begin{cases} \angle O=\angle A=\angle B=90^{\circ} \ \ (1) \\ OA=OB=R \ \ (2) \end{cases}\)
Từ (1) và (2) suy ra OATB là hình vuông \(\Rightarrow S_{OATB}=R^{2}\)
Ta có: \(S_{quat (AOB)}=\dfrac{\pi R^{2}.90}{360}=\dfrac{\pi R^{2}}{4} \ \ (dvdt)\)
\(\Rightarrow S_{quat \ TAB}=S_{OATB}-S_{OAB}=R^{2}-{\dfrac{\pi R^{2}}{4}}={\dfrac{R^{2}}{4}}\big(4-\pi\big) \ \ (dvdt)\)
Câu 47. Cho hai đường tròn (O; 6cm) và (O'; 2cm) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, (B thuộc (O), C thuộc (O') ) Tính số đo các góc ∠AOB, ∠AOC'
A. \(\angle A O B=45^{\circ}\angle A O' C=135^{\circ}\)
B. \(\angle A O B=50^{\circ}\angle A O' C=130^{\circ}\)
C. \(\angle A O B=60^{\circ}\angle A O' C=120^{\circ}\)
D. \(\angle A O B=40^{\circ}\angle A O' C=140^{\circ}\)
.png)
Ta có \(B C\perp O B , B C\perp O'C\) (tiếp tuyến vuông góc với bán kính đi qua tiếp điểm)
\(\Rightarrow \begin{cases} \angle B=\angle C=90^{\circ} \\ OB // O'C \end{cases}\)
Vẽ CD // OO' \((D \in OB)\)
Tứ giác ODCO' là hình bình hành
\(\Rightarrow \begin{cases} CD = OO' = R + R' = 6 + 2 = 8 (cm) \\ BD = OB - OD = 6 - 2 = 4 (cm) \end{cases}\)
\(\Delta BCD\) vuông tại B có CD = 2.BD nên bằng nửa tam giác đều cạnh CD
\(\Rightarrow\angle B D C=60^{\circ}\Rightarrow\angle A O B=\angle B D C=60^{\circ}\) (hai góc đồng vị)
Ta có: \(\angle AOB + \angle AO'C=180^{\circ}\) (hai góc trong cùng phía)
\(\Rightarrow\angle AO'C=180^{\circ} - \angle AOB = 180^{\circ} - 60^{\circ}= 120^{\circ}\)
Vậy \(\angle AOB = 60^{\circ} , \angle AO'C = 120^{\circ}\)
Câu 48. Từ 1 điểm M nằm ngoài đường tròn (O), vẽ hai cát tuyến MAB, MCD (A nằm giữa M và B, C nằm giữa M và D). Cho biết số đo cung nhỏ AC là \(30^o\) và số đo cung nhỏ BD là \(80^o\). Vậy số đo góc M là :
| A. \(50^o\) | B. \(40^o\) | C. \(15^o\) | D. \(25^o\) |
\(\angle M={\dfrac{1}{2}}{\bigg(}s d{\widehat{B D}}-s d{\widehat{A C}}{\bigg)}={\dfrac{1}{2}}.(80^{\circ}-30^{\circ})=25^{\circ}\)
Câu 49. Một hình nón có diện tích xung quanh bằng \(20\pi \ cm^2\) và bán kính đáy 4cm. Đường sinh của hình nón bằng:
| A. 5cm | B. 3cm | C. 4cm | D. 6cm |
Ta có diện tích xung quanh của hình nón
\(S_{xq}=\pi r l\Rightarrow l=\frac{S_{x q}}{\pi r}=\frac{20\pi}{4\pi}=5(c m)\)
Câu 50. Cho hình vuông ABCD nội tiếp đường tròn (O; R), cho hình vuông ABCD quay xung quanh đường trung trực của hai cạnh đối, thì phần thể tích của khối cầu nằm ngoài khối trụ là :
| A. \({\dfrac{\pi R^{3}}{4}}\Bigl(8-3{\sqrt{2}}\Bigr)\) | B. \({\dfrac{\pi R^{3}}{6}}\Bigl(8-3{\sqrt{2}}\Bigr)\) | C. \({\dfrac{\pi R^{3}}{3}}\Bigl(8-3{\sqrt{2}}\Bigr)\) | D. \({\dfrac{\pi R^{3}}{12}}\Bigl(8-3{\sqrt{2}}\Bigr)\) |
Hình vuông ABCD nội tiếp (O; R) nên \(A B=R{\sqrt{2}}\) .Khi quay mô hình ta được :
Hình cầu tâm O bán kính R và hình trụ có chiều cao \(h=R{\sqrt{2}}\), bán kính đáy
\(r=\dfrac {R{\sqrt{2}}}{2}\)
\(V=V_{cau}-V_{tru}=\frac{4}{3}\pi R^{3}-\pi R\sqrt{2}.\dfrac{R^{2}}{2}=\left(\dfrac{8-3\sqrt{2}}{6}\right)\pi R^{3} \ \ (dvdt)\)
Trên đây là 50 câu hỏi trắc nghiệm ôn thi vào lớp 10 năm học 2024 2025 kèm đáp án.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong Ôn thi cấp 3 để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.


