
Mathx.vn biên soạn gửi tới các em hướng dẫn giải chi tiết đề thi tuyển chọn học sinh giỏi cấp tỉnh của sở GDĐT Thanh Hóa môn toán khối THCS năm học 2023 2024. Các em học sinh tải để về làm trước sau đó so sánh kết quả và cách giải chi tiết trong bài viết này. Chúc các em học tập tốt!
Môn thi: Toán - THCS
Năm học: 2023 - 2024
Thời gian làm bài: 150 phút

1. Cho biểu thức:
\({\mathrm{A}}=\left(2-{\dfrac{2{\sqrt{x y}}+1}{1+{\sqrt{x y}}}}+{\dfrac{1}{1-{\sqrt{x y}}}}+{\dfrac{2{\sqrt{x}}}{1-x y}}\right):\left({\dfrac{{\sqrt{x y}}-{\sqrt{x}}}{{\sqrt{x y}}+1}}-{\dfrac{{\sqrt{x y}}+{\sqrt{x}}}{{\sqrt{x y}}-1}}\right)\)
(với \(x > 0, y > 0, xy \neq 1\)). Rút gọn biểu thức A
2. Cho a là số thực thỏa mãn: \(a^{3} - a - 1 = 0\). Tính giá trị của biểu thức
\(B=a\sqrt{2a^{6}-4a^{4}+4a^{2}+3a}-\sqrt{2a^{2}+3a+2}\)
Giải
1.
Ta có:
\({\mathrm{A}}=\left(2-{\dfrac{2{\sqrt{x y}}+1}{1+{\sqrt{x y}}}}+{\dfrac{1}{1-{\sqrt{x y}}}}+{\dfrac{2{\sqrt{x}}}{1-x y}}\right):\left({\dfrac{{\sqrt{x y}}-{\sqrt{x}}}{{\sqrt{x y}}+1}}-{\dfrac{{\sqrt{x y}}+{\sqrt{x}}}{{\sqrt{x y}}-1}}\right)\)
\(= \left(\dfrac{2\Bigl(1+\sqrt{x y}\Bigr)-2\sqrt{x y}-1}{1+\sqrt{x y}}+\dfrac{1}{1-\sqrt{x y}}+\dfrac{2\sqrt{x}}{1-x y}\right) : \left({\dfrac{\left({\sqrt{x y}}-{\sqrt{x}}\right)\left({\sqrt{x y}}-1\right)-\left({\sqrt{x y}}+{\sqrt{x}}\right)\left({\sqrt{x y}}+1\right)}{\left({\sqrt{x y}}+1\right)\left({\sqrt{x y}}-1\right)}}\right) \\ = \left({\dfrac{1}{1 + {\sqrt{x y}}}}+{\dfrac{1}{1 - {\sqrt{x y}}}}+{\dfrac{2{\sqrt{x}}}{1-x y}}\right) : \dfrac{x y-\sqrt{x y}-x\sqrt{y}+\sqrt{x}-x y-\sqrt{x y}-x\sqrt{y}-\sqrt{x}}{x y - 1} \\ = {\dfrac{1-{\sqrt{x y}}+1+{\sqrt{x y}}+2{\sqrt{x}}}{1-x y}} . \dfrac{x y-1}{-2x{\sqrt{y_{-}}}-2{\sqrt{x y}}} \\ = {\dfrac{2+2{\sqrt{x}}}{1-x y}}.{\dfrac{1-x y}{2{\sqrt{x y}}({\sqrt{x}}+1)}} \\ = \dfrac{1}{\sqrt{x y}}\)
Vậy \(A = \dfrac{1}{\sqrt{x y}}\) với \(x > 0, y > 0, xy \neq 1\)
2.
\(B=a\sqrt{2a^{6}-4a^{4}+4a^{2}+3a}-\sqrt{2a^{2}+3a+2} = a{\sqrt{2a^{2}+3a+2(a^{3}-a)^{2}}} - {\sqrt{2a^{2}+3a+2}}\)
\(B = (a - 1) {\sqrt{2a_{-}^{2}+3a+2}}\) (1)
\(B^{2} = (a - 1)^{2} . (2a^{2} + 3a + 2) = \left(a^{2}{-}2a{+}1\right).(2a^{2}{+}3a{+}2) = 2a ^{4} - a ^{3} - 2a ^{2} -a + 2 = \left(2a-1\right)\left(a^{3}- a -1\right) + 1=1\) (2)
Vì \(a(a^{2} - 1) = 1\) nên \(a \neq 0\)
Nếu a < 0 thì \(a(a^{2} - 1) = 1\)
\(\begin{cases}{{a^{2} - 1 <0}}\\ {{a + 1 = a^{3} < 0}}\end{cases} \Rightarrow \begin{cases}{{-1 < a < 1}}\\ {{a < -1}}\end{cases}\) Vô lí
Do đó a > 0. Suy ra: \(a^{3} = a + 1 > 1 \Rightarrow a > 1 \Rightarrow a - 1 > 0 \Rightarrow B > 0\) (3)
Từ (1) (2) (3) suy ra: B = 1
1. Giải phương trình:
\(^3{{\sqrt{x^{3}+5x^{2}}}}-1={\sqrt{{\dfrac{5x^{2}-2}{6}}}}\)
2. Giải hệ phương trình:
Giải
1.
ĐKXĐ: \(x ^ {3} \geq \dfrac {2}{5}\) (*)
Đặt \(t =\,{\sqrt{\dfrac{5x^{2}-2}{6}}}\) (\(t \geq 0\)). Suy ra \(5x^{2} = 6 t^{2} + 2\)
\({^{3}\sqrt{x^{3} + 5x^{2}}} -1=t \Rightarrow x ^ {3} + 6 t^{2} + 2 = {(t+1)^{3}} \Leftrightarrow x ^ {3} = {(t+1)^{3}} \Leftrightarrow x = t - 1 \Leftrightarrow t = x + 1\)
\(\sqrt{\dfrac{5x^{2}-2}{6}}=x+1 \Leftrightarrow \begin{cases}{{x \geq 1}}\\ {{\sqrt{\dfrac{5x^{2}-2}{6}}=(x+1)^2}}\end{cases} \\ \Leftrightarrow \begin{cases}{{x \geq 1}}\\ {{x ^2 + 12x + 8 = 0}}\end{cases} \\ \Leftrightarrow x = -6 + 2\sqrt{7}\)
So sánh với điều kiện (*) thì phương trình có nghiệm là \(x = -6 + 2\sqrt{7}\)
2.
\(\begin{cases}{{x^{2}y^{2}+3x+3y-3=0}} \ \ \ (1) \\ {{x^{3}y-4x^{2}y-3x y^{2}+2x y-x^{2}+x=0}} \ \ \ (2) \end{cases}\)
Lấy phương trình (2) cộng với phương trình (1) theo vế, ta có:
\(x^{2}y^{2}+3x+3y-3 + x^{3}y-4x^{2}y-3x y^{2}+2x y-x^{2}+x = 0 \\ \Leftrightarrow (x^3y+x^2y^2-x^2y)-(x^2+xy-x)-(3x^2y+3xy^2-3xy)+(3x+3y-3)=0 \\ \Leftrightarrow x^2y(x+y-1)-x(x+y-1)-3xy(x+y-1)+3(x+y-1)=0 \\ \Leftrightarrow (x+y-1)(x^2y-3xy-x+3)=0 \Leftrightarrow \left[\begin{array}{c}{{x+y-1=0}}\\ {{(x^2y-3xy-x+3)=0}}\end{array}\right.\)
Với x + y - 1 = 0 => y = 1 - x thế vào (1)
\(\Leftrightarrow x^2(1-x)^2 = 0 \Leftrightarrow \left[\begin{array}{c}{{x=0 \Rightarrow y=1}}\\ {{x=1 \Rightarrow y=0}}\end{array}\right.\)
Với \((x^2y-3xy-x+3)=0 \Leftrightarrow (x-3)(xy-1) = 0 \Leftrightarrow \left[\begin{array}{c}{{x-3=0}}\\ {{xy-1=0}}\end{array}\right. \Leftrightarrow \left[\begin{array}{c}{{x=3}}\\ {{x=\dfrac{1}{y}}}\end{array}\right.\)
Khi x = 3 thế vào (1) \(\Leftrightarrow 9y^3 + 3y+6=0\) (vô nghiệm)
Khi \(x = \dfrac {1}{y}\) thế vào (1) \(\Leftrightarrow 3y^3 - 2y+3=0\) (vô nghiệm)
Vậy tập nghiệm của hệ phương trình là S = {(0;1),(1;0)}
1. Giải phương trình nghiệm nguyên:
\(y={^3{\sqrt{2+{\sqrt{x}}}}}+{^3{\sqrt{2-{\sqrt{x}}}}}\)
2. Cho n là số nguyên dương thỏa mãn \(3^{n} - 1\) chia hết cho \(2^{2024}\).
Chứng minh rằng \(n\geq2^{2022}\)
Giải
1.
\(y={^3{\sqrt{2+{\sqrt{x}}}}}+{^3{\sqrt{2-{\sqrt{x}}}}}\) (1)
ĐKXĐ: \(x \geq 0\)
Nhận thấy: \(y={^3{\sqrt{2+{\sqrt{x}}}}} > {^3{\sqrt{-2+{\sqrt{x}}}}}\) nên
\(y={^3{\sqrt{2+{\sqrt{x}}}}}+{^3{\sqrt{2-{\sqrt{x}}}}} > {^3{\sqrt{-2+{\sqrt{x}}}}}+{^3{\sqrt{2-{\sqrt{x}}}}} = 0 => y > 0\)
Lập phương 2 vế của (1) ta được:
\(y^3=4+3({^3{\sqrt{2+{\sqrt{x}}}}} + {^3{\sqrt{2-{\sqrt{x}}}}}){^3{\sqrt{4-x}}} \Rightarrow y^3=4+3.y.{{^3{\sqrt{4-x}}}} \Rightarrow {{^3{\sqrt{4-x}}}} = \dfrac{y^3-4}{3y}\) (vì y > 0) (2)
Vì \(x \geq 0\) nên \( {{^3{\sqrt{4-x}}}} = \dfrac{y^3-4}{3y} \leq {^3{\sqrt{4}}}\)
=> \(y^3 \leq 3y.{^3{\sqrt{4}}} + 4 \Leftrightarrow y^3 - 3y.{^3{\sqrt{4}}} \leq 4 \Leftrightarrow y(y^2-3.{^3{\sqrt{4}}}) \leq 4\) (*)
Nếu \(y \geq 3\) thì \(y(y^2-3.{^3{\sqrt{4}}}) \geq 3.(9-3.{^3{\sqrt{4}}}) > 4\) mâu thuẫn với (*)
Do đó y < 3 kết hợp vói y > 0 ta được \(y\in\{1,2\}\) vì y nguyên
+. Xét y = 2 thay vào (2) ta được: \({{^3{\sqrt{4-x}}}} = \dfrac {2}{3}\) (vô lý, vì \(x\in Z\) )
+. Xét y = 1 thay vào (2) ta được: \({{^3{\sqrt{4-x}}}} = -1 \Leftrightarrow x = 5\)
Thử lại ta thấy x = 5 và y = 1 thỏa mãn bài toán
Vậy phương trình có nghiệm: (x;y) = (5;1)
2)
Vì n > 0 nên ta đặt \(n = 2^k .m\) (\(k;m \in Z\); m lẻ)
Ta có: \(3^n-1=(3^{2^k})^m -1= (3^{2^k} - 1) ((3^{2^k})^{m-1} + (3^{2^k})^{m-2} + ... +3^{2^k} +1)\)
Do m lẻ nên tổng \((3^{2^k} - 1) ((3^{2^k})^{m-1} + (3^{2^k})^{m-2} + ... +3^{2^k} +1)\) có lẻ số hạng nên tổng đó là số lẻ
Do đó \(3^{n} - 1 \ \vdots \ 2^{2024} \Leftrightarrow 3^{2^k} - 1 \ \vdots \ 2^{2024}\)
Ta lại có:
\((3^{2^k} - 1) = (3-1)(3+1)(3^2+1)(3^{2^2}+1)(3^{2^3}+1)...(3^{2^{k-1}}+1) \\ = 2^3(3^2+1)(3^{2^2}+1)(3^{2^3}+1)...(3^{2^{k-1}}+1)\)
Với \(a \in ({1;2;3;...;k-1})\) , ta có
\(3^{2^k} +1 = [(3^{2^{k-1}})^2-1] + 2 = (3^{2^{k-1}}-1)(3^{2^{k-1}}+1) +2\)
Vì \((3^{2^{k-1}}-1) và (3^{2^{k-1}}+1)\) là các số chẵn nên tích chia hết cho 4
Do đó \(3^{2^k} +1\) chia hết cho 2 nhung không chia hết cho 4
\(\Rightarrow (3^2+1)(3^{2^2}+1)(3^{2^3}+1)...(3^{2^{k-1}}+1) \ \vdots \ 2^{k-1} \\ \Rightarrow 2^3(3^2+1)(3^{2^2}+1)(3^{2^3}+1)...(3^{2^{k-1}}+1) \ \vdots \ 2^{k+2} \\ \Rightarrow 3^n -1 \ \vdots \ 2^{k+2}\)
Để \(3^n -1 \ \vdots \ 2^{2024}\) thì \(2^{k+2} \ \vdots \ 2^{2024}\) => \(k+2 \geq 2024\)
=> \(k \geq 2022\) => \(n=2^k.m \geq 2^k \geq 2^{2022}\)
Vậy ta có điều phải chứng minh
Câu IV (6 điểm)
Cho tam giác đều ABC có độ dài cạnh bằng \(2{\sqrt{3}}\) và đường cao AH. Trên đoạn BH lấy điểm M tùy ý (M không trùng B, H). Gọi P, Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC
1. Chứng minh giá trị của biểu thức MP + MQ không phụ thuộc và vị trí của điểm M
2. Gọi K là trung điểm của AM
a. Chứng minh rằng tứ giác PKQH là hình thoi
b. Gọi S là diện tích hình thoi PKQH. Biết khi điểm M thay đổi thì S nhận đúng một giá trị nguyên dương. Tìm giá trị nguyên dương đó
3. Vẽ đường tròn (O) nội tiếp tam giác ABM. Gọi D, E, F theo thứ tự là tiếp điểm của (O) với các cạnh BM, AB, AM. Vẽ DN vuông góc với EF tại N. Chứng minh \({\widehat{B N E}}={\widehat{M N F}}\)
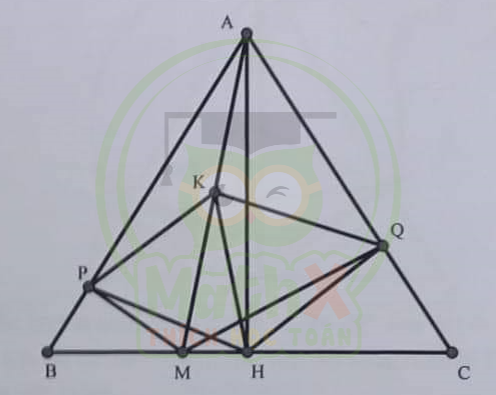
Giải
1.
Trong \(\Delta B M P\) vuông ở P, ta có: \(MP = MB.sinMBP=MB.sin60^0=\dfrac {{\sqrt{3}}}{2}MB\)
Tương tự, ta chứng minh được: \(MQ = \dfrac {{\sqrt{3}}}{2} MC\)
=> \(MP+MQ= \dfrac {{\sqrt{3}}}{2}(MB+MC)=\dfrac {{\sqrt{3}}}{2}BC=\dfrac {{\sqrt{3}}}{2}.2{\sqrt{3}}=3\) không phụ thuộc vào vị trí của điểm M
2.
a.
Do \({\widehat{A P M}}={\widehat{A Q M}} = {\widehat{A H M}} = 90^o\) nên theo tính chất đường trung tuyến của tam giác vuông, ta có
\(KP = KQ = KH = \dfrac {1}{2}AM\) (1)
Trong \(\Delta PKH\) cân ở K có \({\widehat{P K H}}=2{\widehat{P A H}} = 2{\widehat{B A H}} = 2.30^o= 60^o\)
Vậy \(\Delta PKH\) đều => HP = HK (2)
Tương tự, ta chứng minh được \(\Delta QKH\) => HQ = HK (3)
Từ (1) (2) (3) ta được \(HP = PK = KQ = QH = HK = \dfrac {1}{2}AM\) nên tú giác PKQH là hình thoi
b.
Ta có \(S=S_{PKQH}=2S_{PKH}=2.KH^2.\dfrac {{\sqrt{3}}}{4}=\dfrac {{\sqrt{3}}}{2}KH^2=\dfrac {{\sqrt{3}}}{8}AM^2>\dfrac {{\sqrt{3}}}{8}AH^2=\dfrac {9{\sqrt{3}}}{8}\)
\(S=S_{PKQH}=\dfrac {{\sqrt{3}}}{8}AM^2<\dfrac {{\sqrt{3}}}{8}AB^2=\dfrac {3{\sqrt{3}}}{2} \Rightarrow 1,95 \approx \dfrac {9{\sqrt{3}}}{8} < S <\dfrac {3{\sqrt{3}}}{2} \approx 2.60 \Rightarrow S=2\)
3.
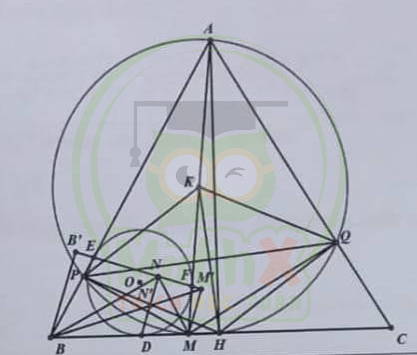
Gọi B', M' lần lượt là hình chiếu của B, M lên EF. Gọi N' là giao điểm của DN và BM'. Khi đó BB' // DN // MM' nên áp dụng định lý Talet trong các \(\Delta BMM'\) ; \(\Delta M'BB'\) ta có:
\(\begin{cases}{\dfrac {MD}{DB}} = \dfrac {M'N'}{N'B} \\ {{\dfrac {M'N'}{N'B} = \dfrac {M'N}{NB'}}}\end{cases} \) => \(\dfrac {BD}{DM} = \dfrac {B'N}{NM'}\) (4)
Xét \(\Delta BB'E\) và \(\Delta MM'F\) , ta có:
\({\widehat{B B' E}}={\widehat{M M' F}} = 90^o\)
\({\widehat{B E B'}}={\widehat{A E F}} = {\widehat{A F E}}\) (\(\Delta AEF\) cân tại F do AE = AF theo tính chất tiếp tuyến) = \( {\widehat{M F M'}}\)
Vậy \({\widehat{B E B'}} \) ~ \({\widehat{M M' F}} \) (g.g) => \(\dfrac {B'E}{M'F} = \dfrac {BE}{MF}= \dfrac {BD}{DM}\) (5) (do BE = BD; MF = MD theo tính chất tiếp tuyến)
Từ (4) và (5), ta được \(\dfrac {B'N}{NM'} = \dfrac {B'E}{M'F}= \dfrac {B'N-B'E}{NM'-M'F}= \dfrac {EN}{FN}\)
Xét \(\Delta BNE\) và \(\Delta MNF\) , ta có:
\({\widehat{B E N}}={\widehat{M F N}}\)
\(\dfrac {EN}{FN} = \dfrac {B'N}{NM'}= \dfrac {BE}{MF}\)
Vậy \(\Delta BNE\) ~ \(\Delta MNF\) (c.g.c) => \({\widehat{B N E}}={\widehat{M N F}}\) (ĐPCM)
Cho a, b, c là các số thực dương thỏa mãn \(a + b + c = {\dfrac{a}{b}}+{\dfrac{b}{c}}+{\dfrac{c}{a}}\)
Tìm giá trị lớn nhất của biểu thức: \(\mathrm{P}={\dfrac{\mathrm{a}+\mathrm{b}+1}{\mathrm{a}^{3}+\mathrm{b}^{3}+1}}+{\dfrac{\mathrm{b}+\mathrm{c}+\mathrm{l}}{\mathrm{b}^{3}+\mathrm{c}^{3}+\mathrm{l}}}+{\dfrac{\mathrm{c}+\mathrm{a}+1}{\mathrm{c}^{3}+\mathrm{a}^{3}+\mathrm{l}}}\)
Giải
Áp dụng bất đẳng thức Cauchy cho giả thiết ta được
\(\mathbf{a}+\mathbf{b}+\mathbf{c}={\dfrac{\mathbf{a}}{\mathbf{b}}}+{\dfrac{\mathbf{b}}{\mathbf{c}}}+{\dfrac{\mathbf{c}}{\mathbf{a}}}\geq 3\)
Mặt khác áp dụng bất đẳng thức Bunhiacopxki dạng phân thức cho giả thiết ta được
\(\mathbf{a}+\mathbf{b}+\mathbf{c}={\dfrac{\mathbf{a}}{\mathbf{b}}}+{\dfrac{\mathbf{b}}{\mathbf{c}}}+{\dfrac{\mathbf{c}}{\mathbf{a}}}\geq \dfrac{\left(a+\mathrm{b}+\mathrm{c}\right)^{2}}{\mathrm{ab+bc+ca}} \Rightarrow ab +bc +ca \geq a + b +c \geq 3\)
Áp dụng bất đẳng thức Bnhiacopxki ta có
\((a^3+b^3+1)(a+b+1) \geq (a^2+b^2+1)^2 \geq \dfrac {(a+b+1)^2(a^2+b^2+1)}{3}\)
Do đó ta được
\(\dfrac {a+b+1}{a^3+b^3+1} \leq \dfrac {3}{a^2+b^2+1}\)
Tương tự ta thu được
\(P \leq \dfrac {3}{a^2+b^2+1} + \dfrac {3}{b^2+c^2+1} + \dfrac {3}{c^2+a^2+1}\)
Ta sẽ chứng minh; \(\dfrac {1}{a^2+b^2+1} + \dfrac {1}{b^2+c^2+1} + \dfrac {1}{c^2+a^2+1} \leq 1\)
Thật vậy, bất đẳng thức trên được viết lại thành
\(\dfrac {a^2+b^2}{a^2+b^2+1} + \dfrac {b^2+c^2}{b^2+c^2+1} + \dfrac {c^2+a^2}{c^2+a^2+1} \geq 2\)
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
\(\dfrac {a^2+b^2}{a^2+b^2+1} + \dfrac {b^2+c^2}{b^2+c^2+1} + \dfrac {c^2+a^2}{c^2+a^2+1} \geq \dfrac { ( \sqrt{a^{2}+b^{2}} + \sqrt{b^{2}+c^{2}} + \sqrt{c^{2}+a^{2}} )^2 }{2(a^2+b^2+c^2)+3}\)
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
\(( \sqrt{a^{2}+b^{2}} + \sqrt{b^{2}+c^{2}} + \sqrt{c^{2}+a^{2}} )^2 \geq 4(a^2+b^2+c^2)+6 \\ \Leftrightarrow {\sqrt{\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)}} + {\sqrt{\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)}} + {\sqrt{\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)}} \geq a^2+b^2+c^2+3\)
Áp dụng bất đẳng thức Bunhiacopxki ta được
\({\sqrt{\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)}} \geq b^2+ac\)
Áp dụng tương tự ta được
\({\sqrt{\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)}} + {\sqrt{\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)}} + {\sqrt{\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)}} \geq a^2+b^2+c^2+ab+bc+ca\)
Mà từ giả thiết ta được \(ab+bc+ca \geq 3\). Do vậy ta được
\({\sqrt{\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)}} + {\sqrt{\left(\mathbf{b}^{2}+\mathbf{c}^{2}\right)\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)}} + {\sqrt{\left(\mathbf{c}^{2}+\mathbf{a}^{2}\right)\left(\mathbf{a}^{2}+\mathbf{b}^{2}\right)}} \geq a^2+b^2+c^2+3\)
Vậy bất đẳng thức được chứng minh
Suy ra giá trị lớn nhất của P là 3
Đẳng thức xảy ra khi và chỉ khi a = b = c = 1
Trên đây MATHX đã hướng dẫn các em chữa đề thi tuyển chọn học sinh giỏi cấp tỉnh của sở GDĐT Thanh Hóa môn toán khối THCS năm học 2023 2024
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
Phụ huynh và các em học có thể tham khảo một số bài toán lớp 9 khác tại đây:
Bài toán về tập hợp và tính chia hết - đề hsg thcs cầu giấy 2023 2024
Một bài toán BĐT hay dùng phương pháp xét bất đẳng thức riêng
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX