
Đội ngũ MATHX biên soạn gửi đến quý phụ huynh và các em học sinh Hướng dẫn giải đề mẫu toán thi vào lớp 6 chất lượng cao THCS Archimedes năm học 2024 - 2025 (Bài nâng cao). Hy vọng rằng tài liệu giải chi tiết này sẽ là một công cụ hữu ích, giúp các em hiểu rõ cấu trúc của đề thi, đồng thời rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động hơn. Chúc em học tốt đạt được những kết quả xuất sắc trong kỳ thi sắp tới và đạt vé vào cổng trường mình mong muốn.
Để biết thêm thông tin về trường và phương thức tuyển sinh Archimedes mới nhất PHHS tham khảo tại đây:
GIỚI THIỆU VỀ TRƯỜNG THCS ARCHIMEDES ACADEMY
THÔNG TIN TUYỂN SINH VÀO LỚP 6 THCS ARCHIMEDES ACADEMY NĂM HỌC 2024 - 2025
Các em học sinh nhấn vào nút tải tài liệu bên dưới để tải đề về làm trước khi xem đáp án để đạt được hiệu quả ôn tập tốt nhất
NĂM HỌC 2024 – 2025
MÔN TOÁN
Phần A. Điền đáp số:
Học sinh ghi kết quả cho 10 bài toán dưới đây
Bài 1. Cho hai số tự nhiên x, y khác 0. Biết rằng 75% của số tự nhiên x bằng 60% của số tự nhiên y, hỏi 40% của số tự nhiên y bằng bao nhiêu phần trăm của số tự nhiên x?
Hướng dẫn:
Vì 75% của số tự nhiên x bằng 60% của số tự nhiên y hay 60% của số tự nhiên y bằng 75% của số tự nhiên x nên:
20% của số tự nhiên y bằng 25% của số tự nhiên x.
Suy ra 40% của số tự nhiên y bằng 50% của số tự nhiên x.
Đáp số: 50% của số tự nhiên x.
Bài 2. Tìm chữ số tận cùng của số
C = (1 + 2 + 3 + … + 9) ´ (9 + 99 + 999 + … + 99…9).
Hướng dẫn:
Có: 1 + 2 + 3 + 4 + … + 9 = 45 nên chữ số tận cùng của dấu ngoặc đầu tiên bằng 5.
Vì số hạng cuối cùng trong dấu ngoặc thứ hai có 2024 chữ số 9
Nên tổng 9 + 99 + 999 + … + 99…9 có 2024 số hạng mà mỗi số hạng đều là số lẻ do đó kết quả của tổng 9 + 99 + 999 + … + 99…9 là một số chẵn.
Vi chữ số tận cùng là 5 nhân với chữ số tận cùng là số chẵn thì chữ số tận cùng là 0 nên chữ số tận cùng của C là 0.
Đáp số: 0.
Nhận xét: Đây là bài toán không khó, biểu thức phía sau có thể làm học sinh mất bình tĩnh khi số lớn quá, tuy nhiên chỗ này chỉ cần xét đến tính chẵn lẻ là được.
Bài 3. Tính giá trị của biểu thức.
\(A =\dfrac{1}{1+\dfrac{1}{2024}}+\dfrac{1}{1+\dfrac{2}{2023}}+\dfrac{1}{1+\dfrac{3}{2022}}+...+\dfrac{1}{1+\dfrac{2024}{1}}\)
Hướng dẫn:
\(A =\dfrac{1}{1+\dfrac{1}{2024}}+\dfrac{1}{1+\dfrac{2}{2023}}+\dfrac{1}{1+\dfrac{3}{2022}}+...+\dfrac{1}{1+\dfrac{2024}{1}}\)
\(A = \dfrac{1}{\dfrac{2025}{2024}}+\dfrac{1}{\dfrac{2025}{2023}}+\dfrac{1}{\dfrac{2025}{2022}}+...+\dfrac{1}{\dfrac{2025}{1}}\)
\(A = \dfrac{2024}{2025}+\dfrac{2023}{2025}+\dfrac{2022}{2025}+...+\dfrac{1}{2025}\)
\(A = \dfrac{1}{2025}\times (2024+2023+2022+...+1)\)
\(A= \dfrac{1}{2025}\times \dfrac{(2024+1)\times 2024}{2}\)
\(A = \dfrac{1}{2025}\times \dfrac{2025\times 2024}{2}\)
\(A = \dfrac{2024}{2} = 1012\)
Vậy A = 1012
Đáp số: 1012
Nhận xét: Ở bài toán này, mấu chốt nằm ở chỗ nhận ra 1 + 2014 = 2 + 2023 = … = 2014 + 1, từ đó biến đổi đưa về cùng mẫu số. Đây cũng là bài toán không quá khó nhưng có thể biểu thức cồng kềnh khiến nhiều học sinh không giải quyết được.
Bài 4. Các số tự nhiên 1, 2, 3, … được điền vào bảng theo quy luật như hình vẽ bên dưới. Hỏi, số được điền ở ô ngoài cùng bên trái của hàng thứ 2023 là số nào?
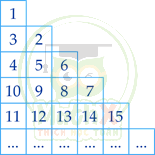
Hướng dẫn:
Số ở ô ngoài cùng hàng thứ nhất là: 1 = 0 + 1
Số ở ô ngoài cùng hàng thứ 3 là: 4 = (1 + 2) + 1
Số ở ô ngoài cùng hàng thứ 5 là: 11 = (1 + 2 + 3 + 4) + 1
Quy luật: Số ở hàng thứ tự lẻ bằng tổng của các số liền trước số thứ tự đó và cộng thêm 1.
Suy ra ô ngoài cùng bên trái của hàng thứ 2023 là:
(1 + 2 + 3 + 4 + … + 2022) + 1 = (1 + 2022) x 2022 : 2 + 1 = 2 045 254.
Đáp số: 2 045 254.
Cách khác: Ta thấy hàng 1 có 1 số, hàng 2 có 2 số, hàng 3 có 3 số…
Ở hàng lẻ, các số được viết tăng dần từ trái qua phải. Ở hàng chẵn, các số được viết tăng dần từ phải qua trái.
Sau khi viết hết 2022 hàng thì ta đã viết đến số:
1 + 2 + 3 + … + 2022 = (1 + 2022) x 2022 : 2 = 2 045 253
Như vậy số đầu tiên bên trái của hàng 2023 là số tiếp theo:
2 045 253 + 1 = 2 045 254.
Đáp số: 2 045 254.
Nhận xét: Đây là bài toán khá hay, không quá khó nhưng đòi hỏi học sinh cẩn thận xử lý thì mới ra kết quả chính xác được.
Bài 5. Một nhóm bốn người đang ngồi với nhau. Mỗi người trong số họ sẽ tính tổng số tuổi của ba người còn lại. Các kết quả thu được lần lượt là 58, 63, 80, 84. Hỏi, tuổi của người nhỏ tuổi nhất trong nhóm là bao nhiêu?
Hướng dẫn:
Ta nhận thấy, tuổi của mỗi bạn đều được xuất hiện ba lần trong ba tổng khi mỗi bạn tính tổng số tuổi của ba bạn còn lại. Do đó ta tính được 3 lần tổng của cả 4 người là:
58 + 63 + 80 + 84 = 285 (tuổi)
Tổng số tuổi của bốn người là: 285 : 3 = 95 (tuổi)
Vì 58 < 63 < 80 < 84 nên tổng số tuổi của 3 người lớn nhất là 84.
Tuổi của người nhỏ nhất trong nhóm là: 95 – 84 = 11 (tuổi)
Đáp số: 11 tuổi.
Nhận xét: Đây là bài toán khá lại, không nhiều bài tư duy và phân tích, tính được tổng của cả 4 người…. Dạng bài ghép cặp, ghép nhóm cũng có khá nhiều bài hay và thú vị, học sinh cần chỉ ra được sự xuất hiện số lần giống nhau của mỗi đại lượng
Bài 6. Một cửa hàng có 6 hòm hàng với khối lượng 316 kg, 327 kg, 336 kg, 338 kg, 349 kg và 351 kg. Cửa hàng đó đã bán 5 hòm hàng và còn thừa lại một hòm hàng, trong đó khối lượng hàng bán được trong buổi sáng gấp bốn lần khối lượng hàng bán được trong buổi chiều. Hỏi, hòm hàng còn lại có khối lượng bao nhiêu ki-lô-gam?
Hướng dẫn:
Vì khối lượng hàng bán được trong buổi sáng gấp 4 lần số lượng hàng bán được trong buổi chiều nên tổng số lượng hàng đã bán được gấp 5 lần khối lượng hàng bán được trong buổi chiều.
Hay tổng khối lượng hàng đã bán được ở 5 hòm là một số chia hết cho 5.
Tổng khối lượng hàng của 6 hòm là: 316 + 327 + 336+338 +349 + 351 = 2017 (kg).
Vì tổng khối lượng của 6 hòm là một số chia cho 5 dư 2, mà tổng khối lượng hàng đã bán được ở 5 hòm là một số chia hết cho 5 nên khối lượng của hòm hàng còn lại là một số chia cho 5 dư 2.
Trong 6 hòm đã cho, chỉ có hòm có khối lượng 327 kg có 327 là số chia cho 5 dư 2 nên hòm hàng còn lại có khối lượng là 327 kg.
Đáp số: 327 kg.
Nhận xét: Đây là bài táon quen thuộc, học sinh hay gặp trong chương trình nâng cao toán 4, khi học về chia hết, bài toán vẽ sơ đồ.
Bài 7. Tính giá trị của biểu thức.
\( N = \dfrac{1}{2}+\dfrac{1+2}{3}+\dfrac{1+2+3}{4}+\dfrac{1+2+3+4}{5}+...+\dfrac{1+2+3+...+100}{101}\)
Hướng dẫn:
\(N = \dfrac{1}{2}+\dfrac{1+2}{3}+\dfrac{1+2+3}{4}+\dfrac{1+2+3+4}{5}+...+\dfrac{1+2+3+...+100}{101} \)
\(N = \dfrac{1}{2}+\dfrac{1}{3}\times (1+2)+\dfrac{1}{4}\times (1+2+3)+\dfrac{1}{5}\times (1+2+3+4)+...+\dfrac{1}{101}\times (1+2+3+...+100)\)
\(N = \dfrac{1}{2}+\dfrac{1}{3}\times \dfrac{(1+2)\times 2}{2}+\dfrac{1}{4}\times \dfrac{(1+3)\times 3}{2}+\dfrac{1}{5}\times \dfrac{(1+4)\times 4}{4}+...+\dfrac{1}{101}\times \dfrac{(1+100)\times 100}{2}\)
\(N = \dfrac{1}{2}+\dfrac{1}{3}\times \dfrac{3\times 2}{2}+\dfrac{1}{4}\times \dfrac{4\times 3}{2}+\dfrac{1}{5}\times \dfrac{5\times 4}{2}+...+\dfrac{1}{101}\times \dfrac{101\times 100}{2}\)
\(N = \dfrac{1}{2}+\dfrac{2}{2}+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{100}{2}\)
\(N = \dfrac{1}{2}\times (1+2+3+4+...+100)\)
\(N = \dfrac{1}{2}\times \dfrac{(1+100)\times 100}{2}\)
\(N = \dfrac{1}{2}\times \dfrac{101\times 100}{2}\)
\(N = \dfrac{101\times 100}{4}\)
\(N = 2525\)
Đáp số: 2525.
Nhận xét: Đây là bài toán dễ kiếm điểm.
Câu 8. Trong hình vẽ bên dưới, có tất cả bao nhiêu tam giác?
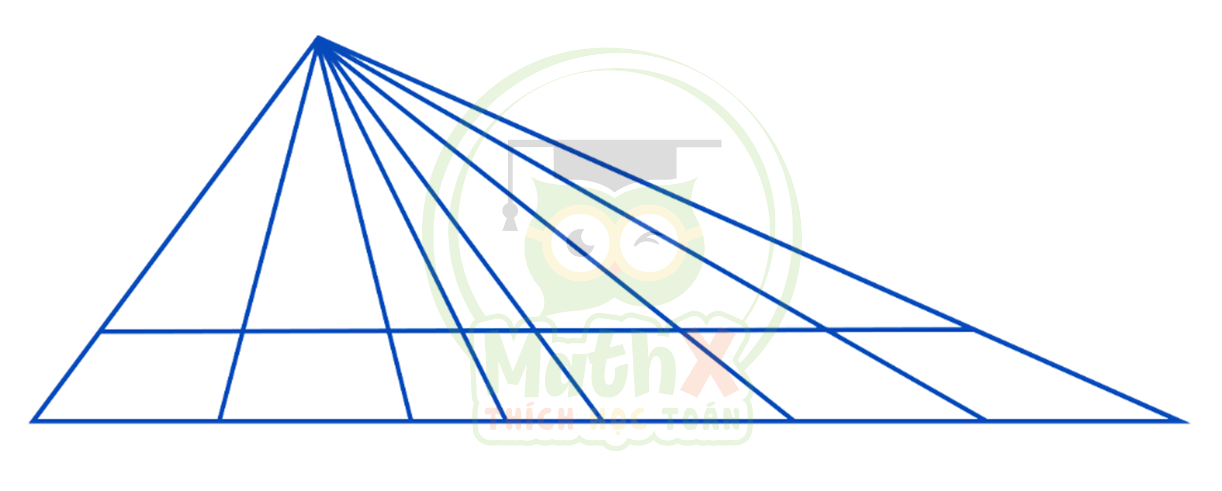
Hướng dẫn:
Ta xét dãy hình có quy luật như sau :
2 tam giác đơn.

Có tổng số tam giác là:
(1 + 2) x 2 : 2 = 3 ( tam giác)
3 tam giác đơn.

Có tổng số tam giác là:
(1 + 3) x 3 : 2 = 6 (tam giác).
4 tam giác đơn.
Có tổng số tam giác là:
(1 + 4) x 4 : 2 = 10 ( tam giác).
7 tam giác đơn.

Có tổng số tam giác là:
(1 + 7) x 7: 2 = 28 (tam giác).
Vậy hình vẽ ở đề bài có số tam giác là : 28 x 2 = 56 (tam giác ).
Đáp số: 56 tam giác.
Nhận xét: Đây là bài toán quen thuộc trong phần chuyên đề đếm hình.
Bài 9. Mật mã mở khóa vali của Nam là một dãy gồm ba chữ số. Dưới đây là một vài thông tin của mật mã.
• Dãy 682 có đúng một chữ số trùng khớp với mật mã và trùng cả vị trí
• Dãy 645 có đúng một chữ số trùng khớp với mật mã nhưng sai vị trí.
• Dãy 206 có hai chữ số trùng khớp với mật mã nhưng cả hai đều sai vị trí.
• Dãy 738 không có chữ số nào trùng khớp với mật mã.
• Dãy 780 có đúng một chữ số trùng khớp với mật mã nhưng sai vị trí.
Hỏi, mật mã mở khóa vali của Nam là dãy số nào?
Hướng dẫn:
Mật mã mở khóa vali của Nam là một dãy gồm ba chữ số.
Vì “Dãy 738 không có chữ số nào trùng khớp với mật mã”
=> Dãy mật mã mở khóa vali của Nam không có các chữ số 7, 3, 8.
Mặt khác, “Dãy 780 có đúng một chữ số trùng khớp với mật mã nhưng sai vị trí”
=> Dãy mật mã mở khóa vali của Nam có chữ số 0 và chữ số 0 nằm ở vị trí thứ ba.
Vì “Dãy 682 có đúng một chữ số trùng khớp với mật mã và trùng cả vị trí’’, mà mật mã không có chữ số 8 nên chữ số đó có thể là 6 hoặc 2.
Nếu chữ số đó là 6 thì 6 trùng khớp với mật mã và ở vị trí thứ nhất.
Lại có: “Dãy 645 có đúng một chữ số trùng khớp với mật mã nhưng sai vị trí” nên chữ số 6 trùng khớp với mật mã nhưng không ở vị trí thứ nhất, mâu thuẫn.
Do đó, “Dãy 682 có đúng một chữ số trùng khớp với mật mã và trùng cả vị trí” là chữ số 2 đứng ở vị trí thứ ba.
“Dãy 206 có hai chữ số trùng khớp với mật mã nhưng cả hai đều sai vị trí” đó là các chữ số 2 và 0 ( vì chữ số 6 không trùng khớp mật mã ).
Vì chữ số 0 sai vị trí, chữ số 0 không đứng ở vị trí thứ ba nên chữ số 0 đứng ở vị trí thứ nhất.
“Dãy 645 có đúng một chữ số trùng khớp với mật mã nhưng sai vị trí” là chữ số 4 hoặc 5 (vì 6 không phải chữ số nằm trong dãy mật mã ). Mặt khác chữ số đó sai vị trí nên nó không thể là chữ số 4.
Do đó chữ số trùng khớp mật mã là chữ số 5, đứng ở vị trí thứ hai.
Vậy mật mã mở khóa vali của Nam là dãy số: 052.
Đáp số: 052
Nhận xét: Bài này khá khó và phức tạp. Tuy nhiên khi làm trắc nghiệm, học sinh cũng có thể thử chọn và suy ra đáp án khá nhanh.
Bài 10.
Trong hình vẽ bên dưới, AE = 2 ´ EC, BF = FE và AG = GF. Biết rằng tam giác GEF có diện tích là 120 cm2, hãy tính diện tích của tam giác ABC.
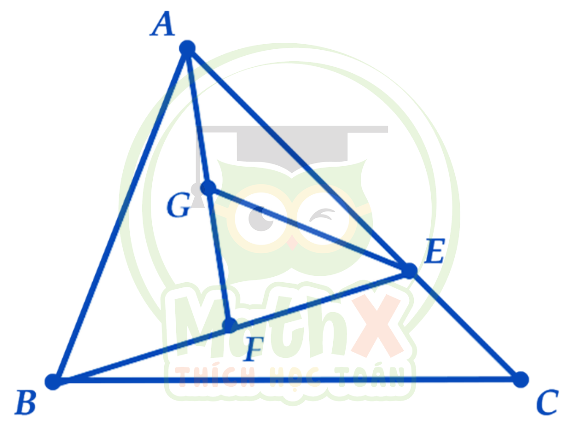
Hướng dẫn:
Có \(AG = GF\) nên \(GF = \dfrac{1}{2} \times AF\).
\(\dfrac{{{S}_{GEF}}}{{{S}_{AEF}}}=\dfrac{GF}{AF}=\dfrac{1}{2}\) (Chung chiều cao từ E hạ xuống đáy AF)
Suy ra diện tích tam giác AEF là:
\(120 \times 2 = 240\) (cm2)
Vì \(BF = FE\) nên \(EF = \dfrac{1}{2} \times EB\).
\(\dfrac{{{S}_{AEF}}}{{{S}_{AEB}}}=\dfrac{EF}{EB}=\dfrac{1}{2}\) (Chung chiều cao từ A hạ xuống đáy BE)
Suy ra diện tích tam giác là:
\(240 \times 2 = 480\) (cm2)
Vì \(AE = 2 \times EC\) nên \(AC = \dfrac{3}{2} \times AE\).
\(\dfrac{{{S}_{ABE}}}{{{S}_{ABC}}}=\dfrac{AE}{AC}=\dfrac{2}{3}\) (Chung chiều cao hạ từ B xuống đáy AC)
Suy ra diện tích tam giác ABC là::
\(480 : 2 \times 3 = 720\) (cm2)
Vậy diện tích tam giác ABC là 720 cm2.
Đáp số: 720 cm2
Phần B. Tự luận.
Học sinh cần trình bày chi tiết lời giải cho 5 bài toán dưới đây.
Bài 11. Tìm tất cả các số tự nhiên n > 1 thỏa mãn
\(\dfrac{1}{1\times 2}+\dfrac{1}{2\times 3}+\dfrac{1}{3\times 4}+...+\dfrac{1}{n\times (n+1)}=\dfrac{2023}{2024}\)
Hướng dẫn:
Ta có:
\(\dfrac{1}{1\times 2}+\dfrac{1}{2\times 3}+\dfrac{1}{3\times 4}+...+\dfrac{1}{n\times (n+1)}=\dfrac{2023}{2024}\)
\(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{4}+...+\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{2023}{2024}\)
\(1-\dfrac{1}{n+1}=\dfrac{2023}{2024}\)
\(1-\dfrac{1}{n+1}=1-\dfrac{1}{2024}\)
Nên \(n + 1 = 2024\) hay \(n = 2023\) .
Đáp số: 2023.
Nhận xét: Đây là bài khá dễ kiếm điểm.
Bài 12. Ở một xứ sở kỳ diệu, các loài vật chung sống hòa bình, hạnh phúc cùng nhau. Một ngày nọ, lợn con đến thăm nhà gia đình gấu. Gia đình gấu có ba thành viên, gồm có gấu bố, gấu mẹ và gấu con. Khi bước vào nhà, lợn con nhìn thấy có ba chú gấu giống hệt nhau: một chú mặc áo sơ mi màu đỏ, một chú mặc áo sơ mi màu xanh dương và một chú mặc áo sơ mi màu xanh lá. Lợn con không thể phân biệt đâu là gấu bố, đâu là gấu mẹ và đâu là gấu con. Hai chú gấu mặc áo sơ mi màu đỏ và màu xanh dương lần lượt mỗi chú nói hai câu, trong đó có một câu đúng và một câu sai.
• Chú gấu mặc áo sơ mi màu đỏ nói: “Tôi là bố của chú gấu mặc áo sơ mi màu xanh dương. Tôi là con gái của chú gấu mặc áo sơ mi màu xanh lá.”
• Chú gấu mặc áo sơ mi màu xanh dương nói: “Hai chú gấu mặc áo sơ mi màu đỏ và màu xanh lá có giới tính khác nhau. Tôi là gấu con.”
Hãy xác định đâu là gấu con.
Hướng dẫn:
Xét hai câu nói của chú gấu mặc áo sơ mi màu đỏ:
Nếu câu: “Tôi là bố của chú gấu mặc áo sơ mi màu xanh dương” là đúng thì bố gấu mặc áo sơ mi màu đỏ và gấu con mặc áo sơ mi màu xanh dương.
Do đó, còn lại gấu mẹ mặc áo sơ mi màu xanh lá.
Từ đó suy ra câu nói “Hai chú gấu mặc áo sơ mi màu đỏ và màu xanh lá có giới tính khác nhau” là đúng.
Do đó câu nói “Tôi là gấu con” của chú gấu mặc áo sơ mi màu xanh dương là sai. Hay gấu con không mặc áo sơ xanh dương (mâu thuẫn).
Vì vậy với hai câu nói của chú gấu mặc áo sơ mi màu đỏ thì câu “Tôi là bố của chú gấu mặc áo sơ mi mà xanh dương là sai.
=> Câu “Tôi là con gái của chú gấu mặc áo sơ mi màu xanh lá” là đúng.
=> Gấu con mặc áo sơ mi màu đỏ.
Vậy chú gấu mặc áo sơ mi màu đỏ là gấu con.
Đáp số: chú gấu mặc áo sơ mi màu đỏ là gấu con.
Nhận xét: Đây là bài toán suy luận logic, cái khó của bài này là học sinh cần trình bày tỉ mỉ, chi tiết để đạt điểm tối đa trong bài toán này.
Câu 13. Cho bảng ô vuông như hình vẽ bên dưới. Người ta điền các số tự nhiên 1, 2, …, 16 vào các ô vuông của bảng, mỗi ô vuông được điền đúng một số và mỗi số chỉ được dùng đúng một lần, sao cho tổng của tất cả các số ở mỗi hàng và ở mỗi cột là như nhau (có tất cả hai hàng và hai cột). Gọi N là tổng của bốn số được điền vào bốn ô vuông ở góc của bảng. Hãy tìm giá trị nhỏ nhất của N.
Hướng dẫn:
Gọi T là tổng của tất cả các số ở mỗi hàng hay mỗi cột.
Khi đó ta có:
\(T \times 4 = N + (1+2+3 \ + \ ... \ +16)\)
\(T \times 4 = N + (1+16) \times 16 : 2\)
\(T \times 4 = N + 136\)
Vì \(T \times 4\) và \(N + 136\) đều chia hết cho 4 nên N phải chia hết cho 4.
Tổng của 4 số nhỏ nhất trong các số tự nhiên từ 1 đến 16 là \(1+2+3+4=10\)
Do đó N lớn hơn hoặc bằng 10
Vì N chia hết cho 4 và N lớn hơn hoặc bằng 10 nên N nhỏ nhất bằng 12.
Suy ra: Bốn số được điền vào bốn ô vuông ở góc của bảng có thể là 1, 2, 3, 6
(vì \(1+2+3+6=12\) ).
Tổng của tất cả các số ở mỗi hàng hay mỗi cột là:
\((12+136):4=37\).
Ví dụ ta có các cách sắp xếp các số 1, 2, 3, …, 16 vào bảng thỏa mãn yêu cầu bài toán với N nhỏ nhất bằng 12 như sau:
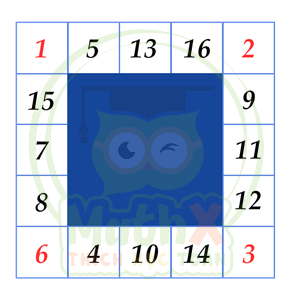
Đáp số: Giá trị nhỏ nhất của N = 10.
Nhận xét: bài này khá khó, nhưng cũng không quá lạ lẫm khi học sinh được tiếp xúc với dạng toán về “ma phương”. Mấu chốt của bài toán nằm ở chỗ các ô ở góc xuất hiện 2 lần. Cần khai thác điểm này và tính chia hết cho 4 khi tính tổng của cả 4 hàng.
Bài 14. Một số tự nhiên được gọi là số palindrome nếu đọc theo chiều xuôi hay chiều ngược thì đều như nhau (chẳng hạn, 131, 1221, 14841, … là các số palindrome). Một số tự nhiên có sáu chữ số \(\overline{abcdef}\) được gọi là số thú vị nếu \(\overline{cd}\) chia hết cho \(\overline{ab}\) và \(\overline{ef}\) chia hết cho \(\overline{ab}\) (chẳng hạn 124896, 102040, … là các số thú vị). Một số tự nhiên có sáu chữ số được gọi là số palindrome thú vị nếu nó vừa là số palindrome vừa là số thú vị. Hãy tìm tất cả các số tự nhiên có sáu chữ số là số palindrome thú vị.
Hướng dẫn:
Số tự nhiên có sáu chữ số là số palindrome sẽ có dạng là: \(\overline{abccba}\) (a, b, c là các chữ số và a khác 0).
Để \(\overline{abccba}\) là số thú vị thì \(\overline{cc}\) chia hết cho \(\overline{ab}\) và \(\overline{ba}\) chia hết cho \(\overline{cc}\) .
Vì \(\overline{ba}\) chia hết cho \(\overline{cc}\) suy ra \(b=a\) . Khi đó ta được số \(\overline{aaccaa}\) .
Vì \(\overline{cc}\) chia hết cho \(\overline{aa}\) và \(\overline{cc}\) chia hết cho \(\overline{aa}\) nên \(\overline{aa} = \overline{cc}\) . Suy ra \(a=c\) .
Do đó số tự nhiên có sáu chữ số là số palindrome thú vị nếu số đó có tất cả các chữ số giống nhau và khác 0.
Vậy các số tự nhiên có có sáu chữ số là số palindrome thú vị là:
111111; 222222; 333333; 444444; 555555; 666666; 777777; 888888; 999999.
Đáp số: 111111; 222222; 333333; 444444; 555555; 666666; 777777; 888888; 999999.
Nhận xét: Đây là bài toán không quá khó, nhưng việc hiểu kỹ và phân tích đúng đề bài là rất cần thiết để giải đúng bài toán này.
Bài 15. Các thành viên của câu lạc bộ thuyền máy Archimedes muốn thực hiện một cuộc thi vòng quanh một hồ lớn hình tròn bằng thuyền máy. Có một khó khăn là mỗi thuyền máy đều chỉ có thể mang tối đa số nhiên liệu đủ cho nửa đường đi. Cuối cùng, họ thống nhất cuộc thi như sau: Tất cả các đội sẽ cùng xuất phát tại cùng một điểm. Mỗi đội đều có thể dùng nhiều thuyền máy tham dự cuộc thi, các thuyền máy có thể tiếp nhiên liệu cho nhau nhưng không được đậu lại vào bờ dọc đường đi mà đều phải đi tiếp hoặc quay về điểm xuất phát. Thuyền nào khi quay về điểm xuất phát có thể nạp thêm nhiên liệu và tiếp tục xuất phát. Đội thắng là đội có được một thuyền máy chạy liên tục hết một vòng hồ để trở về điểm xuất phát. MATHSISFUN là một trong các đội tham gia cuộc thi. Chứng minh rằng, bằng cách dùng ba thuyền máy, MATHSISFUN sẽ có cách chiến thắng cuộc thi. (Giả thiết rằng, thời gian tiếp nhiên liệu mỗi lần là không đáng kể và các thuyền máy đều có tốc độ như nhau.)
Hướng dẫn:
Ta xét ba tàu là A, B, C.
Chia đường đua thành 8 phần bằng nhau như hình vẽ dưới đây. Không mất tính tổng quát, ta giả sử nhiên liệu để đi hết cả vòng đua là 8 lít xăng. Khi đó mỗi tàu chỉ chứa được tối đa là 4 lít xăng (do chỉ chứa được nhiên liệu để đi được nửa chặng đường)
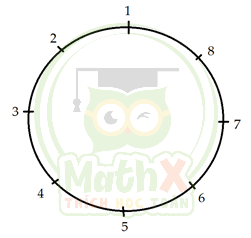
Bước 1: Cho ba tàu đi từ vạch xuất phát số 1, theo đến địa điểm số 2.
Tại địa điểm số 2, mỗi tàu còn lại 3 lít xăng.
Tàu C cho tàu A 1 lít xăng à tàu A có 4 lít
Tàu C cho tàu B 1 lít xăng à tàu B có 4 lít
Tàu C còn lại 3 – 1 – 1 = 1 lít xăng.
Bước 2:
Tàu A, B đi tiếp đến vị trí số 3. Lúc này tàu A, B còn 3 lít xăng.
Tại vị trí số 3, tàu B cho tàu A 1 lít xăng à tàu A lại có 4 lít xăng.
Tàu B còn lại 2 lít xăng.
Tàu C quay về vị trí 1. Tàu C hết xăng và nhận thêm 4 lít xăng mới.
Bước 3.
Tàu A (đang còn 4 lít xăng) đi tiếp đến vị trí số 5 và tại đây tàu A còn lại 2 lít xăng.
Tàu B còn lại 2 lít xăng đi về số 1 thì hết xăng, đổ thêm 4 lít xăng.
Tàu C ở vị trí 1 nhận thêm 4 lít xăng và đợi cho đến khi tàu B về vị trí số 1.
Bước 4.
Tàu A đi tiếp đến vị trí số 6. Tàu A còn 1 lít xăng.
Tàu B và C cùng đi đến vị trí số 8. Tại đây, tàu C cho tàu B 1 lít xăng. Tàu B còn lại 4 lít, tàu C còn lại 2 lít xăng.
Bước 5.
Tàu A đi tiếp đến vị trí số 7. Tàu A hết xăng. Tàu A nhận của tàu B 1 lít xăng, tàu A có 1 lít xăng.
Tàu B đi tiếp đến số 7. Tàu B còn lại 3 lít xăng. Tàu B cho tàu A 1 lít xăng. Tàu B còn lại 2 lít.
Tàu C quay về số 1. Tàu C đổ thêm cho đầy 4 lít xăng.
Bước 6.
Tàu A đi tiếp đến số 8, tàu A lại hết xăng. Tại vị trí 8, tàu A nhận 1 lít xăng từ tàu C.
Tàu B đi về số 8, tàu B còn 1 lít.
Tàu C đi đến số 8, tàu C còn 3 lít xăng. Tàu C cho tàu A 1 lít xăng.
Bước 7.
Cả ba tàu từ vị trí 8 về vị trí số 1.
Nhận xét: Đây là bài toán khó, rất khó trong thời gian 90 phút và với tư duy của học sinh tiểu học. Có lẽ đây là bài phân loại cao của đề thi này.
Trên đây MATHX đã Hướng dẫn giải đề mẫu toán thi vào lớp 6 chất lượng cao THCS Archimedes năm học 2024 - 2025 (Bài nâng cao). Chúc các em học và ôn tập thật tốt
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS ARCHIMEDES ACADEMY được đội ngũ MATHX biên soạn, đầy đủ và chi tiết nhất để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Phụ huynh và các em học sinh xem thêm chủ đề giải đề Archimedes tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG ARCHIMEDES 2020 (BÀI CƠ BẢN)
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG ARCHIMEDES 2020 (BÀI NÂNG CAO)
ĐỀ MẪU (CÓ ĐÁP ÁN) 50 BÀI TOÁN RÀ SOÁT KIẾN THỨC TIỂU HỌC ARCHIMEDES SCHOOL NĂM HỌC 2024 2025