ĐỀ MẪU (CÓ ĐÁP ÁN) 50 BÀI TOÁN RÀ SOÁT KIẾN THỨC TIỂU HỌC ARCHIMEDES SCHOOL NĂM HỌC 2024 2025 - MATHX

 

Đội ngũ MATHX biên soạn gửi đến các em đề mẫu 50 bài toán rà soát kiến thức trường tiểu học Archimedes năm học 2024 - 2025. Các đề mẫu chỉ mang tính tham khảo không phải đề thi chính thức, mục đích tổng hợp kiến thức toán khối tiểu học để các em ôn tập và làm bài tốt. Các em học sinh xem câu hỏi và làm trước sau đó đối chiếu kết quả và cách giải chi tiết trong bài viết này để đạt được hiệu quả ôn tập tốt nhất. Chúc các em học tốt!

 

Để biết thêm thông tin chi tiết về trường và phương thức tuyển sinh vào 6 trường THCS Archimedes, quý phụ huynh tham khảo tại đây: ĐÔI NÉT GIỚI THIỆU VỀ TRƯỜNG THCS ARCHIMEDES ACADEMY

 

Các em học sinh tải đề về làm sau đó so sánh với kết quả bên dưới. Phía dưới cùng bài viết có đính kèm Video chữa đề của thầy Hiếu, các em xem video nghe thầy giảng để tiếp thu và tích lũy được nhiều kiến thức hơn

 

 

 

 

HỆ THỐNG GIÁO DỤC ARCHIMEDES SCHOOL

50 bài toán rà soát kiến thức

Khối Tiểu học | Môn Toán | Thời gian 60’ | Mã đề Demo

 

 

 

Bài 1: Số “Bốn triệu năm trăm nghìn” có bao nhiêu chữ số 0?

 

Giải

Ta viết số “Bốn triệu năm trăm nghìn” ra giấy: 4.500.000

=> Có 5 số 0

 

Đáp số: 5 số 0

 

 

Bài 2: Tính: 34 567 + 82 164 + 17 836 + 15 433.

 

Giải

34 567 + 82 164 + 17 836 + 15 433

= 34 567 + 15 433 + 82 164 + 17 836

= 50 000 + 100 000

= 150 000

 

Đáp số: 150 000

 

 

Bài 3: Trong một phép trừ, số bị trừ gấp đôi số trừ. Biết hiệu của phép trừ là 570, tìm số bị trừ.

 

Giải

Giả sử ta gọi số trừ là 1 phần

Vậy theo đề bài số bị trừ sẽ là 2 phần

Hiệu của phép trừ là 570

=> 1 phần sẽ = 570

=> Số bị trừ = 2 phần = 2 x 570 = 1140

 

Đáp số: 1140

 

 

Bài 4: Một số chia cho 9 được thương bằng 15 và dư 5. Tìm số đó.

 

Giải

Ta sẽ giải bài toán bằng cách lấy: thương x số chia + số dư

15 x 9 + 5

= 135 + 5

= 140

 

Đáp số: 140

 

 

 

Bài 5: Cần bao nhiêu chữ số để viết các số tự nhiên liên tiếp từ 1 đến 20?

 

Giải

Ta xét các số từ:

1 -> 9: có 9 số có 1 chữ số

10 -> 20: có 11 số có 2 chữ số

Vậy số chữ số cần để viết các số tự nhiên liên tiếp từ 1 -> 20 ta làm như sau:

1 x 9 + 2 x 11 = 9 + 22 = 31 (chữ số)

 

Đáp số: 31 chữ số

 

 

 

Bài 6: Tính \({\dfrac{2}{9}}\times{\dfrac{18}{15}}\times{\dfrac{10}{4}}.\)

 

Giải

\({\dfrac{2}{9}}\times{\dfrac{18}{15}}\times{\dfrac{10}{4}} \\ = {\dfrac{2}{9}}\times{\dfrac{2 \times 9}{3 \times 5}}\times{\dfrac{2 \times 5}{2 \times 2}} \\ = \dfrac {2 \times 2 \times 9 \times 2 \times 5}{9 \times 3 \times 5 \times 2 \times 2} \\ = {\dfrac{2}{3}}\)

 

Đáp số: \({\dfrac{2}{3}}\)

 

 

Bài 7: Tìm x biết \({\dfrac{1}{5}}+x={\dfrac{3}{7}}.\)

 

Giải

\({\dfrac{1}{5}}+x={\dfrac{3}{7}} \\ \Leftrightarrow x = {\dfrac{3}{7}} - {\dfrac{1}{5}} \\ \Leftrightarrow x = {\dfrac{15}{35}} - {\dfrac{7}{35}} \\ \Leftrightarrow x = {\dfrac{8}{35}}\)

 

Đáp số: \({\dfrac{8}{35}}\)

 

 

 

Bài 8: Viết phân số bằng phân số \(\dfrac{2}{3}\), có mẫu số bằng 18.

 

Giải

\(\dfrac{2}{3} = \dfrac{?}{18}\)

\(\Leftrightarrow \dfrac{2}{3} = \dfrac{2 \times 6}{3 \times 6} = \dfrac{12}{18}\)

 

Đáp số: \(\dfrac{12}{18}\)

 

 

Bài 9: Số nào lớn nhất trong các số:\({\dfrac{14}{3}};4{\dfrac{1}{7}};{\dfrac{9}{2}};3{\dfrac{9}{10}}\) ?

 

Giải

Ta có:

\({\dfrac{14}{3}} = 4{\dfrac{2}{3}}\)

\({\dfrac{14}{3}} = 4{\dfrac{1}{2}}\)

\(3{\dfrac{9}{10}} < 4\) (loại)

=> Ta chỉ cần so sánh 3 số còn lại là \(4{\dfrac{2}{3}} , 4{\dfrac{1}{7}}, 4{\dfrac{1}{2}}\) và có thể thấy thấy số \(4{\dfrac{2}{3}}\)  là lớn nhất

=> Số lớn nhất trong dãy số trên là: \({\dfrac{14}{3}}\)

 

Đáp số: \({\dfrac{14}{3}}\)

 

 

 

Bài 10: Cho dãy các phân số có quy luật sau: \({\dfrac{1}{2}};\;{\dfrac{1}{3}};\;{\dfrac{2}{3}};\;{\dfrac{1}{4}};\;{\dfrac{1}{4}};\;{\dfrac{1}{5}};\;{\dfrac{2}{5}};\;{\dfrac{3}{5}};\;{\dfrac{4}{5}};...\)

Viết phân số thứ 15 trong dãy.

 

Giải

Theo đề bài ta thấy:

- Mẫu số là 2 ta có 1 phân số là \(\dfrac {1}{2}\)

- Mẫu số là 3 ta có 2 phân số là \(\dfrac {1}{2}, \dfrac {2}{3}\)

- Mẫu số là 4 ta có 3 phân số là \(\dfrac {1}{4}, \dfrac {2}{4}, \dfrac {3}{4}\)

- Mẫu số là 5 ta có 4 phân số là \(\dfrac {1}{5}, \dfrac {2}{5}, \dfrac {3}{5}, \dfrac {4}{5} \)

- Vậy mẫu số là 6 ta có 5 phân số là \(\dfrac {1}{6}, \dfrac {2}{6}, \dfrac {3}{6}, \dfrac {4}{6}, \dfrac {5}{6}\)

Ta thấy khi mẫu số đến 5 thì đã có 10 phân số rồi

=> phân số thứ 15 trong dãy trên là số:  \(\dfrac {5}{6}\)

 

 

Đáp số: \(\dfrac {5}{6}\)

 

 

Bài 11: Viết số 0,24 dưới dạng phân số tối giản.

 

Giải

\(0,24 = \dfrac {24}{100} = \dfrac {6}{25}\)

 

Đáp số: \(\dfrac {6}{25}\)

 

 

Bài 12: Điền số thích hợp với chỗ chấm: 3 tạ 20 kg = … tấn.

 

Giải

Đổi 3 tạ = 300 kg

300 kg + 20 kg = 320 kg = 0,32 tấn

 

Đáp số: 0,32 tấn

 

 

Bài 13: Tìm a biết: 

 

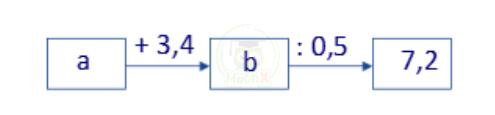
Giải

Bài toán này ta tính ngược lại:

\(7,2 \times 0,5 = \dfrac {72}{10} \times \dfrac {5}{10} = \dfrac {360}{100} = 3,6\)

3,6 - 3,4 = 0,2

 

Đáp số: a = 0,2

 

 

Bài 14: Tính: 5,12 × 4,5 + 4,88 × 4,5.

 

Giải

5,12 × 4,5 + 4,88 × 4,5

= 4,5 x (5,12 + 4,88)

= 4,5 x 10

= 45

 

Đáp số: 45

 

 

Bài 15: Chỉ từ các chữ số 3; 4; 7, viết được bao nhiêu số thập phân lớn hơn 4 có các chữ số khác nhau và có hai chữ số ở phần thập phân?

 

Giải

Theo đề bài, các số cần tìm lớn hơn 4 nên sẽ là các số sau:

4,37 ; 4,73 ; 7,34 ; 7,43

=> ta viết được 4 số

 

Đáp số: Viết được 4 số

 

 

Bài 16: Một cuộn dây dài 6 m được cắt ra thành 15 đoạn bằng nhau. Hỏi mỗi đoạn dây dài bao nhiêu mét?

 

Giải

Ta có độ dài mỗi đoạn là:

\(6 : 15 = \dfrac {6}{15} = 0,4\) (m)

 

Đáp số: 0,4 m

 

 

Bài 17: Trung bình cộng hai số là 5,64. Biết hiệu của hai số là 4,2, tìm số bé.

 

Giải

Từ trung bình cộng ta tính được tổng của 2 số là:

5,64 x 2 = 11,28

Theo đề bài ta biết hiệu của 2 số = 4,2

=> Số bé là: (11,28 - 4,2) : 2 = 7,08 : 2 = 3,54

=> Số lớn là: 11,28 - 3,54 = 7,74

 

Đáp số: 

Số bé = 3,54

Số lớn = 7,74

 

 

Bài 18: \(\dfrac{4}{7}\) của một số bằng 140. Tìm số đó.

 

Giải

Theo đề bài ta có số đó bằng:

\(140 : \dfrac {4}{7} = 140 \times \dfrac {7}{4} = 35 \times 7 = 245\)

 

Đáp số: 245

 

 

 

Bài 19: Hằng có một số hình dán, Hằng đã cho bạn \(\dfrac{1}{2}\) số hình dán đó và cho thêm 1 cái nữa thì còn lại 11 cái. Hỏi lúc đầu Hằng có bao nhiêu hình dán?

 

Giải

Số hình dán Hằng có trước khi cho thêm 1 cái là:

11 + 1 = 12 (cái)

Số hình dán Hằng có lúc đầu là:

12 x 2 = 24 (cái)

 

Đáp số: 24 cái

 

 

Bài 20: Một người mua 5 quyển vở và 10 cái bút hết tất cả 95 000 đồng. Hỏi quyển vở giá bao nhiêu tiền biết rằng mua một quyển vở và một cái bút hết 14 000 đồng?

 

Giải

1 vở 1 bút hết 14 000 đồng

=> 5 vở 5 bút sẽ hết: 14 000 x 5 = 70 000 (đồng)

Mà 5 vở 10 bút hết 95 000 đồng

=> 5 bút sẽ có giá: 95 000 - 70 000 = 25 000 (đồng)

=> 1 bút sẽ có giá: 25 000 : 5 = 5 000 (đồng)

=> 1 quyển vở có giá: 14 000 - 5000 = 9 000 (đồng)

 

Đáp số: 9 000 đồng

 

 

Bài 21: Trong một vườn cây, \(\dfrac{1}{3}\) số cây là cây cam, còn lại là 20 cây chanh. Hỏi có bao nhiêu cây cam trong vườn?

 

Giải

Ta có \(\dfrac{1}{3}\) số cây là cây cam, còn lại là cây chanh

=> \(\dfrac{2}{3}\) số cây sẽ là cây chanh

Ta có 20 cây chanh sẽ tương ứng với \(\dfrac{2}{3}\) số cây trong vườn

=> Ta tính được tất cả số cây trong vườn là:

20 : \(\dfrac{2}{3}\) = 30 (cây)

=> Số cây cam có trong vườn là:

30 - 20 = 10 (cây)

 

Đáp số: 10 cây

 

 

Bài 22: Anh hơn em 8 tuổi. Biết rằng hiện nay tuổi em bằng \(\dfrac{3}{5}\) tuổi anh, tính tuổi của anh hiện nay.

 

Giải

Đây là bài toán biết hiệu và biết tỉ số

Ta có:

- Tuổi của em là 3 phần

- Tuổi của anh là 5 phần

Anh hơn em 8 tuổi

=> Ta tính được số tuổi của anh hiện nay là:

8 : (5 - 3) x 5 = 8 : 2 x 5 = 20 (tuổi)

 

Đáp số: 20 tuổi

 

 

Bài 23: Nếu 5 người làm trong 5 ngày thì sửa được 75 m đường. Hỏi 9 người làm trong 6 ngày thì sửa được bao nhiêu mét đường? (Biết năng suất của mỗi người như nhau).

 

Giải

Đây là bài toán tỉ lệ thuận tỉ lệ nghịch

Ta tính được số mét đường 9 người làm trong 6 ngày là

\(75 \times \dfrac {9}{5} \times \dfrac {6}{5} = 3 \times 9 \times 6 = 162\) (m)

 

 

Đáp số: 162 m

 

 

 

Bài 24: Mỗi chai sữa có 0,5 lít sữa, mỗi lít sữa cân nặng 1,08 kg, mỗi vỏ chai cân nặng 0,1 kg. Hỏi 100 chai sữa đó cân nặng bao nhiêu ki-lô-gam?

 

Giải

Ta có cân nặng của \(\dfrac {1}{2}\) lít sữa là:

1,08 x \(\dfrac {1}{2}\) = 0,54 (kg)

Ta tính tiếp cân nặng của 1 chai sữa là:

0,54 + 0,1 = 0,64 (kg)

Cân nặng của 100 chai sữa là:

100 x 0,64 = 64 (kg)

 

Đáp số: 64 kg

 

 

Bài 25: Cho một số có ba chữ số. Nếu xóa chữ số hàng trăm thì số đã cho bị giảm đi 7 lần. Tìm số đã cho.

 

Giải

Gọi số đã cho là: \(\overline {abc}\)

Theo đề bài ta có:

\(\overline {abc} = \overline {bc} \times 7 \\ \Rightarrow a \times 100 + \overline {bc} = \overline {bc} \times 7 \\ \Rightarrow a \times 100 = \overline {bc} \times 6 \\ \Rightarrow a \times 50 = \overline {bc} \times 3 \\ \Rightarrow a = 3 \ và \ \overline {bc} = 50\)

=> số đó là 350

 

Đáp số: 350

 

 

Bài 26: Chu vi một hình chữ nhật bằng chu vi một hình vuông có diện tích 49 \(cm^2\). Biết chiều dài hơn chiều rộng 4 cm, tính diện tích hình chữ nhật.

 

Giải

Ta có diện tích hình vuông là 49 \(cm^2\)

=> cạnh hình vuông sẽ = 7 cm  (vì 7 x 7 = 49)

Ta tính được chu vi hình vuông là:

7 x 4 = 28 (cm)

=> nữa chu vi hình chữ nhật là:

28 : 2 = 14 (cm)

Mà ta có hiệu của chiều dài và chiều rộng = 4 cm

=> Chiều dài hình chữ nhật là:

(14 + 4) : 2 = 9 (cm)

=> Chiều rộng hình chữ nhật là:

14 - 9 = 5 (cm)

Diện tích hình chữ nhật là:

9 x 5 = 45 (\(cm^2\))

 

 

Đáp số: 45 \(cm^2\)

 

 

 

Bài 27: Hình bình hành ABCD có AB = 4 cm, AH = 3 cm, DH = 1 cm. Tính diện tích hình thang AHCB.

 

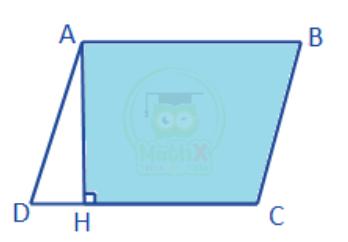
Giải

Theo hình vẽ và dữ kiện đề bài, Ta tính được

CH = 4 - 1 = 3 (cm)

=> diện tích hình thang AHCB là:

"Đáy lớn đáy nhỏ ta đem cộng vào rồi nhân với chiều cao chia đôi lấy nửa thế nào cũng ra"

(3 + 4) x 3 : 2 = 10,5 (\(cm^2\))

 

 

Đáp số: 10,5 \(cm^2\)

 

 

 

Bài 28: Đường kính của một bánh xe đạp là 70 cm. Bánh xe lăn được 1 000 vòng thì xe đạp đi được bao nhiêu mét?

 

Giải

Ta có chu vi bánh xe đạp hình tròn chính là quảng đường bánh xe lăn được 1 vòng

=> Bánh xe lăn được 1 vòng sẽ đi được:

3,14 x 70 = 219,8 (cm)

Bánh xe lăn được 1000 vòng thì đi được:

219,8 x 1000 = 219 800 (cm) = 2198 (m)

 

Đáp số: 2198 m

 

 

Bài 29: Cho hình chữ nhật ABCD có AB = 45 cm, AD = 30 cm, BM = \(\dfrac{2}{3}\) AB, ND = \(\dfrac{1}{2}\) AN. Tính diện tích tam giác NCM.

 

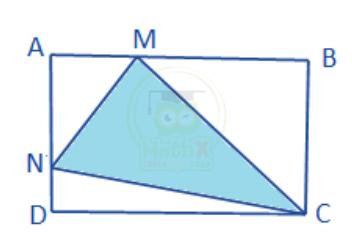
Giải

Ta có: BM = \(\dfrac{2}{3}\) AB

=> AB là 3 phần thì BM là 2 phần và AM là 1 phần

=> AB = 45 x \(\dfrac{1}{3}\) = 15 (cm)

MB = 45 - 15 = 30 (cm)

 

ND = \(\dfrac{1}{2}\) AN

Gọi AD gồm 3 phần thì ND là 1 phần và AN là 2 phần

=> ND = 30 x \(\dfrac{1}{3}\) = 10 (cm)

AN = 30 - 10 = 20 (cm)

Để tính diện tích tam giác MNC (là phần xanh đậm) ta sẽ lấy diện tích hình chữ nhật ABCD trừ đi diện tích các phần còn lại

\(S_{ABCD} = 45 \times 30 = 1350 (cm^2)\)

\(S_{NDC} = 45 \times 10 : 2 = 225 (cm^2)\)

\(S_{AMN} = 20 \times 15 : 2 = 150 (cm^2)\)

\(S_{BMC} = 30 \times 30 : 2 = 450 (cm^2)\)

\(S_{MMC} = S_{ABCD} - S_{NDC} - S_{AMN} - S_{BMC} = 1350 - 225 - 150 - 450 = 525 (cm^2)\)

 

Đáp số: 525 \(cm^2\)

 

 

 

Bài 30: Cho tam giác ABC có diện tích bằng 48 cm2 . Biết D là trung điểm BC, AE = \(\dfrac{1}{2}\) BE, FC = \(\dfrac{1}{3}\) AF, tính diện tích tứ giác AFDE.

 

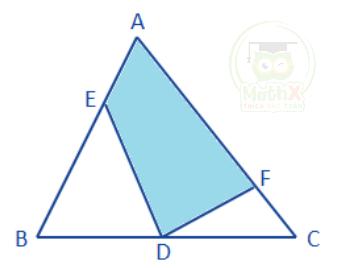
Giải

Ta có thể giải tương tự như bài 29 nhưng thầy Hiếu sẽ hướng dẫn cho cấc em một cách giải khác nhanh hơn. Chi tiết về cách giải này, thầy Hiếu sẽ nói rõ trong Video được đính kèm ở bên dưới, các em chú ý theo dõi nhé.

Vì đây là bài toán trắc nghiệm, nên ta sẽ áp dụng cách tính mẹo (nếu thi tự luận các em sẽ phải trình bày đầy đủ). Các em nhớ là cách làm dưới đây chỉ áp dụng để tính nhanh khi làm trắc nghiệm và các em không được phép làm như thế này khi trình bày bài tự luận

Áp dụng tỉ số diện tích tam giác ta có:

\(S_{CFD} = \dfrac {CF}{CA} \times \dfrac {CD}{CB} \times S_{ABC} = \dfrac {1}{4} \times \dfrac {1}{2} \times 48 = 6 (cm^2)\)

 

\(S_{BED} = \dfrac {BE}{BA} \times \dfrac {BD}{BC} \times S_{ABC} = \dfrac {2}{3} \times \dfrac {1}{2} \times 48 = 16 (cm^2)\)

 

=> \(S_{AEDF} = S_{ABC} - S_{BED} - S_{CFD} = 48 - 16 - 6 = 26 (cm^2)\)

 

 

Đáp số: \(S_{AEDF} = 26 cm^2\)

 

 

 

Bài 31: Nếu cạnh của hình lập phương được gấp lên 3 lần thì diện tích toàn phần của hình lập phương gấp lên bao nhiêu lần?

 

Giải

Ta có công thức tính diện tích toàn phần của hình lập phương là:

a x a x 6   (trong đó a là cạnh của hình lập phương)

Nếu gấp cạnh lên 3 lần thì công thức phía trên sẽ trở thành:

(a x 3) x (a x 3) x 6 -> diện tích toàn phần sẽ gấp lên: 3 x 3 = 9 (lần)

 

Đáp số: 9 lần

 

 

Bài 32: Hình bên được xếp từ các khối lập phương nhỏ giống nhau từng lớp theo quy luật. Nhìn từ trên xuống theo chiều mũi tên, lớp thứ nhất ở trên cùng gồm có 2 khối lập phương nhỏ. Nếu tiếp tục xếp như vậy thì lớp thứ 4 sẽ có bao nhiêu khối lập phương nhỏ?

 

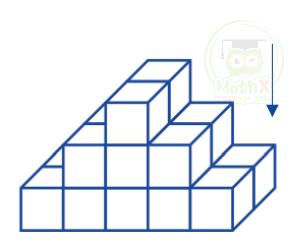
Giải

Hình vẽ trên nhìn từ trên xuống theo chiều mũi tên, ta có:

Lớp thứ nhất trên cùng gồm 2 khối

Lớp thứ 2 gồm 2 x 3 = 6 khối

Lớp thứ 3 gồm 2 x 5 = 10 khối

Vậy lớp thứ 4 sẽ gồm: 2 x 7 = 14 khối lập phương nhỏ

 

Đáp số: 14 khối

 

 

Bài 33: Hình hộp chữ nhật có chiều rộng bằng 4 cm, chiều dài gấp 2 lần chiều rộng, chiều cao ngắn hơn chiều dài 2 cm. Tính thể tích hình hộp chữ nhật.

 

Giải

Chiều dài hình hộp chữ nhật là:

4 x 2 = 8 (cm)

Chiều cao hình hộp chữ nhật là:

8 - 2 = 6 (cm)

Thể tích hình hộp chữ nhật là:

4 x 8 x 6 = 192 (\(cm^3\))

 

Đáp số: 192 \(cm^3\)

 

 

Bài 34: Tính thể tích hình lập phương biết hiệu của diện tích toàn phần và diện tích xung quanh là 50 \(cm^2\) .

 

Giải

Chúng ta chú ý:

Diện tích toàn phần của hình lập phương gồm 6 mặt và có công thức: a x a x 6

Diện tích xung quanh của hình lập phương gồm 4 mặt và có công thức: a x a x 4

Theo dữ kiện đề bài ta có:

(a x a x 6) - (a x a x 4) = a x a x 2 = 50

=> a x a = 50 : 2 = 25

=> a = 5 (cm)

Thế tích hình lập phương là:

5 x 5 x 5 = 125 (\(cm^3\))

 

Đáp số: 125 \(cm^3\)

 

 

Bài 35: Một bể cá hình hộp chữ nhật có kích thước trong lòng bể là: chiều dài 3 m, chiều rộng 2 m, mức nước có trong bể cao 0,5 m. Người ta thả vào bể một hòn đá làm hòn non bộ thì mức nước trong bể cao 0,6 m. Tính thể tích phần hòn non bộ ngập trong bể nước.

 

Giải

Ta thấy thể tích phần hòn non bộ ngập trong bể nước chính là phần mà làm cho nước dâng lên

Ta tính được chiều cao của mức nước dâng lên là:

0,6 - 0,5 = 0,1 (m)

Thể tích phần làm cho nước dâng lên sẽ bằng chiều dài bể x chiều rộng bể x chiều cao của mức nước dâng lên = 3 x 2 x 0,1 = 0,6 ( \(m^3\))

 

Đáp số: 0,6  \(m^3\)

 

 

Bài 36: Biết 7% của một số là 21. Tìm số đó.

 

Giải

Số đó là:

21 : 7% = 21 : 7 x 100 = 300

 

Đáp số: 300

 

 

Bài 37: Biết 70% cơ thể con người là nước, nếu một người nặng 60 kg thì bao nhiêu ki-lô-gam cơ thể là nước?

 

Giải

Số kg cơ thể là nước của 1 người nặng 60kg là:

60 x 70% = 60 x 70 : 100 = 4200 : 100 = 42 (kg)

 

Đáp số: 42 kg

 

 

Bài 38: 40% số học sinh của lớp 5A là nữ. Biết lớp có 15 học sinh nam, hỏi lớp có tất cả bao nhiêu học sinh?

 

Giải

40% số học sinh là nữ vậy 60% số học sinh còn lại sẽ là nam

Vậy 15 học sinh nam sẽ ứng với 60% số học sinh của lớp

Vậy cả lớp có tất cả:

15 : 60% = 15 x 100 : 60 = 25 (học sinh)

 

 

Đáp số: 25 học sinh

 

 

Bài 39: Một chiếc tủ lạnh được giảm giá 20% so với giá ban đầu thì có giá 4 000 000 đồng. Hỏi giá ban đầu trước khi được giảm của chiếc tủ lạnh là bao nhiêu?

 

Giải

Tủ lạnh giảm 20% tức là còn 80%

80% chiếc tủ lạnh tương ứng với giá là 4 000 000 đồng

=> Giá ban đầu của chiếc tủ lạnh là:

4 000 000 : 80% = 4 000 000 x 100 : 80 = 5 000 000 (đồng)

 

Đáp số: 5 000 000 đồng

 

 

Bài 40: Lãi suất tiết kiệm là 0,5% một tháng. Một người gửi tiết kiệm 10 000 000 đồng. Hỏi sau một tháng cả số tiền gửi và tiền lãi là bao nhiêu?

 

Giải

10 000 000 đồng tiền gửi sẽ ứng với 100% số tiền

Sau 1 tháng lãi 0,5% vậy số tiền lãi sau 1 tháng là:

10 000 000 x 0,5% = 10 000 000 x 0,5 : 100 = 50 000 (đồng)

Vậy cả tiền gửi và tiền lãi sau 1 tháng là:

10 000 000 + 50 000 = 10 050 000 (đồng)

 

Đáp số: 10 050 000 đồng

 

 

Bài 41: Điền vào chỗ chấm: 5 giờ 45 phút + 2 giờ 35 phút = ... giờ… phút.

 

Giải

5 giờ 45 phút + 2 giờ 35 phút = 8 giờ 20 phút.

 

Đáp số: 8 giờ 20 phút.

 

 

Bài 42: Điền vào chỗ chấm: 5 m/s = … km/giờ.

 

Giải

Đối \(5 \ m/s = \dfrac {5 \times \dfrac {1}{1000}km}{\dfrac{1}{3600}giờ} = \dfrac {5 \times 3600}{1000} = 18 km/giờ\)

 

Đáp số: 18 km/giờ

 

 

Bài 43: Tú đi từ nhà đến trường hết 15 phút với vận tốc 3 km/giờ. Hỏi quãng đường từ nhà Tú đến trường dài bao nhiêu mét?

 

Giải

Đôi 15 phút = \(\dfrac {1}{4}\) giờ

Quãng đường từ nhà Tú tới trường dài:

\(\dfrac {1}{4} \times 3km/giờ = 0,75 km = 750 (m)\)

 

Đáp số: 750 m

 

 

Bài 44: Tàu đi từ thành phố A đến thành phố B trong 5 tiếng. Biết hai thành phố cách nhau 160 km, tính vận tốc của tàu.

 

Giải

Vận tốc của tàu là:

160 : 5 = 32 (km/giờ)

 

Đáp số: 32 km/giờ

 

 

Bài 45: Một xe máy đi từ A và dự định đến B lúc 8 giờ 30 phút. Nhưng khi đi được 5 km thì phải quay lại A và dừng lại ở A 10 phút. Sau đó xe máy tiếp tục đi và đến B lúc 9 giờ. Tìm vận tốc của xe máy biết vận tốc xe máy không đổi trên toàn bộ đường đi.

 

Giải

Với bài toán này các em theo dõi kĩ video thầy Hiếu giảng phía bên dưới để có thể tư duy một cách dễ hiểu nhất.

Phân tích đề bài: Đi được 5km thì phải quay lại A và dừng lại ở A 10 phút sau đó mới đi lại từ đầu là đi từ A đến B

=> Quãng đường đi thêm lãng phí sẽ là 5km đầu tiên và 5km quay đầu ngược trở về là 10km

Thời gian thực tế so với thời gian dự định cách nhau: 9 giờ - 8 giờ 30 phút = 30 (phút)

Vậy tổng thời gian đi 5km rồi quay về và nghỉ 10 phút là 30 phút

=> Thời gian xe máy đi 10km sẽ mất 30 - 10 = 20 phút = \(\dfrac {1}{3}\) giờ

=> Vận tốc của xe máy là:

10 : \(\dfrac {1}{3}\) = 30 (km/giờ)

 

 

Đáp số: 30 km/giờ

 

 

Bài 46: Tính: \(9999{\dfrac{8}{9}}+999{\dfrac{8}{9}}+99{\dfrac{8}{9}}+9{\dfrac{8}{9}}+{\dfrac{4}{9}}\,.\)

 

Giải

\(9999{\dfrac{8}{9}}+999{\dfrac{8}{9}}+99{\dfrac{8}{9}}+9{\dfrac{8}{9}}+{\dfrac{4}{9}}\, \\ = 9999{\dfrac{8}{9}}+999{\dfrac{8}{9}}+99{\dfrac{8}{9}}+9{\dfrac{8}{9}}+\dfrac{1}{9} +\dfrac{1}{9}+\dfrac{1}{9}+\dfrac{1}{9} \\ = 9999{\dfrac{8}{9}} +\dfrac{1}{9} +999{\dfrac{8}{9}}+\dfrac{1}{9}+99{\dfrac{8}{9}}+\dfrac{1}{9}+9{\dfrac{8}{9}}+\dfrac{1}{9} \\ = 9999{\dfrac{9}{9}}+999{\dfrac{9}{9}}+99{\dfrac{9}{9}}+9{\dfrac{9}{9}} \\ = 10000 + 1000 + 100 + 10 \\ = 11110\)

 

Đáp số: 11110

 

 

Bài 47: Từ 4 chữ số 0; 1; 2; 3 lập được bao nhiêu số có ba chữ số khác nhau chia hết cho 3?

 

Giải

Ta lấy những nhóm số chia hết cho 3 gồm có:

0; 1; 2 (0 + 1 + 2 = 3 chia hết cho 3) và 1; 2; 3 (1 + 2 + 3 = 6 chia hết cho 3)

Nhóm 0; 1; 2 ta lập được: 4 số chia hết cho 3

Nhóm 1; 2; 3 ta lập được: 6 số chia hết cho 3

Vậy tổng cộng ta lập được: 4 + 6 = 10 số chia hết cho 3

 

Đáp số: 10 số

 

 

Bài 48: Cô giáo chia kẹo cho học sinh. Nếu mỗi học sinh được chia 3 cái thì cô vẫn còn 30 cái kẹo. Nếu mỗi học sinh được chia 4 cái thì cô chỉ còn 4 cái kẹo. Hỏi cô giáo có bao nhiêu cái kẹo?

 

Giải

Đây là bài toán thừa thiếu

Nếu chia mỗi hs 3 cái kẹo thì cô còn thừa 30 cái kẹo

Nếu chia mỗi hs 4 cái kẹo thì cô còn thừa 4 cái kẹo

Hay khi còn còn 30 cái kẹo cô cho thêm mỗi hs 1 cái thì cô còn 4 cái kẹo

=> Số kẹo cô đã cho thêm là: 30 - 4 = 26 (cái kẹo)

Cô cho thêm mỗi hs 1 cái kẹo tức là cho 26 cái kẹo sẽ tương ứng với 26 hs

=> số kẹo ban đầu của cô giáo là:

26 x 3 + 30 = 108 (cái kẹo)

 

Đáp số: 108 cái kẹo

 

 

Bài 49: An, Bình, Cường, Dũng so sánh chiều cao của mình.

An nói: “Tớ cao nhất.”

Bình nói: “Tớ không phải là người thấp nhất.”

Cường nói: “Tớ không cao bằng An nhưng có một người thấp hơn tớ.”

Dũng nói: “Tớ thấp nhất.”

Biết rằng có 1 bạn nói dối, hỏi bạn nào cao nhất?

 

Giải

Với câu hỏi này các em học sinh xem video thầy Hiếu giảng bên dưới để hiểu rõ được bài toán nhất

Theo đề bài ta có 1 bạn nói dối nên ta sẽ xét từng trường hợp 1

- TH1: An nói dối => 3 bạn còn lại nói thật

Ta có thứ tự từ cao đến thấp như sau:

Binh, An, Cường, Dũng

- TH2: Bình nói dối => 3 bạn còn lại nói thật

Bình là người thấp nhất nhưng Dũng cũng nói mình thấp nhất (mâu thuẫn -> loại)

- TH3: Cường nói dối => 3 bạn còn lại nói thật

Tương tự TH2 thì trong TH này Cường cao nhất mà An cũng nói mình cao nhất (mâu thuẫn -> loại)

- TH4: Dũng nói dối => 3 bạn còn lại nói thật

Tương tự TH này Dũng cao nhất mà An cũng cao nhất (mâu thuẫn -> loại)

=> Chỉ có TH1 thỏa mãn. Vậy Bình cao nhất

 

Đáp số: Bình

 

 

Bài 50: Cho 22 tấm thẻ được viết các số tự nhiên liên tiếp từ 1 đến 22. Lấy 2 thẻ số khác nhau ghép lại để tạo 1 phân số. Cứ như vậy sẽ có 11 phân số được tạo ra. Hỏi có thể tạo được nhiều nhất bao nhiêu phân số có giá trị bằng một số tự nhiên?

 

Giải

2 thẻ số khác nhau ghép lại tạo thành 1 phần số

Vậy ta có thể ghép được: 22 : 2 = 11 phân số bất kì

Phân số có giá trị bằng số tự nhiên tức là tử số cần chia hết cho mẫu số

Ta xét số 13; 17; 19. 3 số này chỉ có thể ghép với 1 để thành phân số có giá trị bằng số tự nhiên

Ví dụ ta lấy số \(\dfrac {13}{1}\) thì sẽ loại đi 2 số còn lại là 17 và 19

=> Ta sẽ dùng 22 - 2 = 20 số để ghép phân số và sẽ ghép được 20 : 2 = 10 phân số có giá trị bằng số tự nhiên

Các phân số đó là:

\(\dfrac {13}{1}, \dfrac {4}{2}, \dfrac {21}{3}, \dfrac {15}{5}, \dfrac {12}{6}, \dfrac {14}{7}, \dfrac {16}{8}, \dfrac {18}{9}, \dfrac {20}{10}, \dfrac {22}{11}\)

 

Vậy có thể tạo được nhiều nhất 10 phân số có giá trị bằng số tự nhiên với dãy số trên

 

 

Đáp số: 10 phân số

 

 

Để nâng cao kỹ năng giải bài ngoài việc học trên lớp, các em nên tham khảo thêm một số tài liệu bổ trợ và làm bài tập phần đề thi năm trước. Ngoài ra các em học sinh tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS ARCHIMEDES ACADEMY để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.

 

 

Các em học sinh xem Video thầy Hiếu chữa đề phía bên dưới để hiểu hơn về đề thi: