
Đội ngũ MATHX biên soạn gửi đến quý phụ huynh và các em học sinh hướng dẫn giải đề luyện tập toán ôn thi lớp chọn thcs archimedes 2024 - đề 01. Đây là tài liệu được chính MATHX biên soạn dựa trên đề thi của những năm trước nhằm mục đích giúp các em học sinh hiểu rõ cấu trúc của đề thi, đồng thời rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động hơn. Chúc em học tốt đạt được những kết quả xuất sắc trong kỳ thi sắp tới.
Để biết thêm thông tin về trường và phương thức tuyển sinh Archimedes mới nhất PHHS tham khảo tại đây:
GIỚI THIỆU VỀ TRƯỜNG THCS ARCHIMEDES ACADEMY
THÔNG TIN TUYỂN SINH VÀO LỚP 6 THCS ARCHIMEDES ACADEMY NĂM HỌC 2024 - 2025
Các em học sinh nhấn vào nút tải tài liệu bên dưới để tải đề về làm trước khi xem đáp án để đạt được hiệu quả ôn tập tốt nhất
Thời gian làm bài: 90 phút
Chú ý: Đề biên soạn với độ khó và thời gian phù hợp tính chất thi lớp chọn. Đề lớp chọn của Archimedes không có format cố định qua các năm. Phụ huynh cho con tham khảo và làm đề để ôn tập kiến thức và rèn luyện thêm kỹ năng làm bài.
Phần A. Các bài toán trắc nghiệm điền đáp số (1 điểm/bài)
Bài 1. Tính \(20,2 \times 89 + 0,03 \times 89 + 20,23 \times 11\)
Hướng dẫn:
\(20,2 \times 89 + 0,03 \times 89 + 20,23 \times 11 \\ = 89 \times (20,2 + 0,03) + 20,23 \times 11 \\ = 89 \times 20,23 + 20,23 \times 11 \\ = 20,23 \times (89 + 11) \\ = 20,23 \times 100 \\ = 2023\)
Đáp số: 2023.
Bài 2. Một hình chữ nhật có diện tích bằng 588cm2 và chiều rộng bằng \(\dfrac {3}{4}\) chiều dài. Tính chu vi của hình chữ nhật đó.
Hướng dẫn:
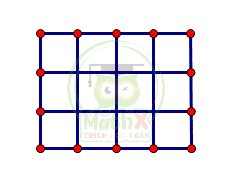
Ta có hình chữ nhật như hình vẽ, chia chiều dài thành 4 phần chiều rộng thành 3 phần
Như hình vẽ ta thấy mỗi 1 ô vuông nhỏ đều là 1 phần của diện tích hình chữ nhật lớn, chúng ta có tất cả:
\(4 \times 3 = 12\) (ô vuông)
Diên tích của 1 ô vuông nhỏ là:
\(588 : 12 = 49 (cm^2)\)
Ta có: \(49 = 7 \times 7\) nên cạnh của ô vuông = 7cm
=> Ta tính được chiều dài của hình chữ nhật là:
\(7 \times 4 = 28\) (cm)
Chiều rộng của hình chữ nhật là:
\(7 \times 3 = 21\) (cm)
=> Chu vi hình chữ nhật là:
\((28 + 21) \times 2 = 98\) (cm)
Đáp số: 98cm.
Bài 3. Một xe lửa vượt qua cái cầu dài 450m mất 45 giây, vượt qua cột điện mất 15 giây và vượt qua 1 người đi xe đạp cùng chiều mất 25 giây. Tính vận tốc của người đi xe đạp?
Hướng dẫn:
Chú ý dữ kiện đầu bài cho là xe lửa vượt qua cầu dài 450m mất 45 giây nghĩa là 45 giây xe lửa đi được 450m + chiều dài của xe lửa
Nếu coi cột điện có đường kính không đáng kể thì quãng đường xe lửa vượt qua cột điện trong 15 giây chính bằng chiều dài của xe lửa
=> Như vậy thời gian để xe lửa đi qua cầu là:
\(45 - 15 = 30\) (s)
=> Vận tốc của xe lửa là:
\(450 : 30 = 15\) (m/s)
Quãng đường xe lửa vượt qua cột đèn là:
\(15 \times 15 = 225\) (m)
=> Tàu lửa dài 225 m (Vận tốc tàu x thời gian đi hết độ dài của tàu)
Gọi T là thời gian để xe lửa vượt qua cột điện, S là quảng đường đi, Vt là vận tốc xe lửa, Vx là vận tốc xe đạp
Để vượt qua người đi xe đạp cùng chiều tức vựơt qua quãng đường bằng độ dài của tàu phải mất thời gian là
\(T = S (Vt - Vx)\)
\(=> 25 = 225 : (15 - Vx) \\ => 15 – Vx = 9 \\ => Vx = 15 - 9 = 6 \ (m/s)\)
=> Vận tốc của người đi xe đạp là 6m/s
Đáp số: 6m/s
Bài 4. Cho các số có dạng \(\overline {a435b}\) có các chữ số khác nhau và chia hết cho 15. Tính tổng các số đó.
Hướng dẫn:
Chú ý từ khóa “các chữ số khác nhau”
Theo dữ kiện đề bài, ta có số đó chia hết cho 15
Ôn lại kiến thức, các số chia hết cho 3 và chia hết cho 5 sẽ chia hết cho 15
Các số có chữ số tận cùng bằng 0 hoặc bằng 5 thì sẽ chia hết cho 5
=> b = 0 hoặc b = 5 (loại vì theo đề bài số cần tìm có các chữ số khác nhau)
=> b = 0
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3
=> a = 3 (loại vì trùng) ; a = 6 hoặc a = 9
=> Ta tìm được 2 số: 64350 và 94350
=> Tổng của 2 số đó là:
64350 + 94350 = 158700
Đáp số: 158700.
Bài 5. Tìm các chữ số a, b khác 0 thỏa mãn:
\(a \times b \times \overline {ab} = \overline {bbb}\)
Hướng dẫn:
\(a \times b \times \overline {ab} = \overline {bbb} b \times 111 \\ => a \times b \times \overline {ab} = b \times 111 \\ => a \times \overline {ab} = 111 \\ => a \times \overline {ab} = 3 \times 37 \\ => a = 3 ; b = 7\)
Đáp số: a = 3 ; b = 7.
Bài 6. Xếp các hình lập phương cạnh 1 cm thành một hình hộp chữ nhật có chiều dài 15cm, chiều rộng 10cm, chiều cao 7cm rồi sơn hết cả 6 mặt hình vừa xếp được. Hỏi có bao nhiêu hình lập phương nhỏ được sơn 2 mặt?
Hướng dẫn:
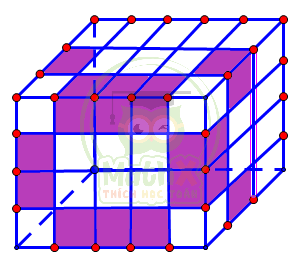
Chúng ta chú ý những hình lập phương được sơn 2 mặt là những hình lập phương nằm ở cạnh, sát với đỉnh và khác đỉnh
Ta có số hình lập phương nhỏ được sơn 2 mặt là:
\((15 - 2) \times 4 + (10 – 2) \times 4 + (7 – 2) \times 4 = 52 + 32 + 20 = 104\)
Đáp số: 104 hình lập phương.
Bài 7. Tìm giá trị của a biết:
\(\dfrac{1}{1 + \dfrac{1}{2 + \dfrac{1}{a + \dfrac{1}{2}}}} = \dfrac {16}{23}\)
Hướng dẫn:
Đặt cả cụm
\(1 + \dfrac{1}{2 + \dfrac{1}{a + \dfrac{1}{2}}} = A\)
\(=> \dfrac {1}{A} = \dfrac {16}{23}\)
\(=> A = 1 : \dfrac {16}{23} = \dfrac {23}{16} = 1 + \dfrac {7}{16}\)
Ta có:
\(A = 1 + \dfrac {7}{16}\)
\(=> 1+ \dfrac{1}{2 + \dfrac{1}{a + \dfrac{1}{2}}} = 1 + \dfrac {7}{16}\)
\(=> \dfrac{1}{2 + \dfrac{1}{a + \dfrac{1}{2}}} = \dfrac {7}{16}\)
\(=> 2 + \dfrac {1}{a + \dfrac {1}{2}} = \dfrac {16}{7} = 2 + \dfrac {2}{7}\)
\(=> 2 + \dfrac {1}{a + \dfrac {1}{2}} = 2 + \dfrac {2}{7}\)
\(=> \dfrac {1}{a + \dfrac {1}{2}} = \dfrac {2}{7}\)
\(=> a + \dfrac {1}{2} = \dfrac {7}{2}\)
\(=> a = 3\)
Đáp số: 3.
Câu 8. Người ta dùng các chữ số 2; 0; 1; 6 để tạo thành dãy các số tự nhiên khác 0 sắp xếp theo thứ tự tăng dần: 1; 2; 6; 10; 11; 12; 16; 20; 21; 22; 26; …
Hỏi số thứ 66 là số nào?
Hướng dẫn:
Từ các chữ số 2; 0; 1; 6 tạo được 3 số tự nhiên có 1 chữ số: 1; 2; 6
Từ các chữ số 2; 0; 1; 6 tạo được số các số tự nhiên có 2 chữ số \(\overline {ab}\)
(\(a \neq 0\)) là: \(3 \times 4 = 12\) (số)
Từ các chữ số 2; 0; 1; 6 tạo được số các số tự nhiên có 3 chữ số \(\overline {abc}\) (\(a \neq 0\)) là: \(3 \times 4 \times 4 = 12\) (48 số)
Tổng số các số tự nhiên có 1, 2 và 3 chữ số được tạo từ các chữ số 2; 0; 1; 6 là: 3 + 12 + 48 = 63 (số)
3 số tự nhiên tiếp theo trong dãy số là các số tự nhiên có 4 chữ số được tạo từ các chữ số 2; 0; 1; 6 lần lượt là
1 000; 1 001; 1 002.
Số thứ 66 trong dãy số là 1 002.
Đáp số: 1 002.
Bài 9. Hai máy cùng gặt xong một thửa ruộng hết 12 giờ. Nếu máy I gặt một mình trong 4 giờ, rồi máy II gặt tiếp thêm 9 giờ nữa thì được \(\dfrac {7}{12}\) thửa ruộng. Hỏi nếu máy I gặt một mình thì gặt xong thửa ruộng trong bao lâu?
Hướng dẫn:
1 giờ 2 máy cùng gặt đc:
\(1 : 2 = \dfrac {1}{12}\) (thửa ruộng)
Nếu máy I gặt một mình trong 4 giờ, rồi máy II gặt tiếp thêm 9 giờ. Ta có thể coi như dữ kiện này như sau:
Máy I và máy II cùng làm trong 4 giờ và máy 2 làm một mình trong 5 giờ
=> Trong khoảng thời gian 4 giờ thì cả 2 máy gặt được:
\(\dfrac {1}{12} \times 4 = \dfrac {4}{12} = \dfrac {1}{3}\) (thửa ruộng)
Trong khoảng thời gian 5 tiếng máy 2 gặt được
\(\dfrac {7}{12} - \dfrac {1}{3} = \dfrac {3}{12} = \dfrac {1}{4}\) (thửa ruộng)
=> Trong 1 giờ thì máy II gặt được:
\(\dfrac {1}{4} : 5 = \dfrac {1}{20}\) (thửa ruộng)
=> Trong 1 giờ thì máy I gặt được:
\(\dfrac {1}{12} - \dfrac {1}{20} = \dfrac {2}{60} = \dfrac {1}{30}\) (thửa ruộng)
=> Máy I cần: \(30 \times 1 = 30\) (giờ) để gặt 1 mình xong thửa ruộng
Đáp số: 30 giờ
Bài 10. Cho tam giác ABC. Lấy N trên đoạn AB, M trên đoạn BC sao cho: NA = 2NB; MC = 2MB. O là giao điểm của AM và CN Tính diện tích BNOM biết diện tích tam giác AON là \(8cm^2\).
Hướng dẫn:
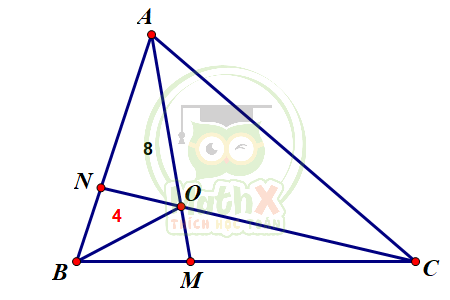
Ta có \(BM = \dfrac {1}{3} BC\)
\(=> S_{ABM} = \dfrac {1}{3} S_{ABC}\) (chung chiều cao hạ từ A và \( BM = \dfrac {1}{3} BC\))
Tương tự ta chứng minh được:
\(S_{CBN} = \dfrac {1}{3} S_{ABC}\) (chung chiều cao hạ từ C và \(BN = \dfrac {1}{3} AB\))
\(=> S_{ABM} = S_{CBN} = \dfrac {1}{3} S_{ABC}\)
Xét \(\Delta {ABM}\) và \(\Delta {CBN}\) đều có chung tứ giác BNOM
\(S_{ABM} = S_{CBN}\)
\(=> S_{COM} = S_{AON} = 8 (cm^2)\)
Ta có \(S_{AON} = 8 (cm^2)\)
\(=> S_{BON} = 4 (cm^2)\) (vì \(BN = \dfrac {1}{2} AN\))
Tương tự ta chứng minh được:
\(S_{BOM} = 4 (cm^2)\) (vì \(BM = \dfrac {1}{2} CM\))
\(=> S_{BNOM} = S_{BON} + S_{BOM} = 4 + 4 = 8 (cm^2)\)
Đáp số: 8cm2
Phần B. Các bài toán tự luận.
Học sinh cần trình bày chi tiết lời giải cho 5 bài toán dưới đây.
Bài 11. Giá nhập vào của một chiếc Tivi là 4.800.000 đồng. Ở cửa hàng, chiếc tivi được ghi giá tăng 20% so với giá nhập, tuy nhiên thực tế khi bán chỉ bán được với giá 75% giá định bán. Hỏi cửa hàng đó lỗ bao nhiêu tiền khi bán ti vi đó?
Hướng dẫn:
Cách 1:
Giá được ghi để bán (niêm yết) là:
\(4800000 \times 120\% = 5760000\) (đồng)
Giá thực tế bán được là:
\(5760000 \times 75\% = 4320000\) (đồng)
Cửa hàng lỗ số tiền là:
\(4800000 – 4320000 = 480000\) (đồng)
Cách 2:
Cửa hàng mong muốn bán giá tang 20% nghĩa là cửa hàng muốn bán:
\(100 \% + 20 \% = 120 \%\) giá trị chiếc TV
Ta có giá bán thực tế so với giá mong muốn là:
\(120 \% \times 75 \% = 90 \%\) giá trị chiếc TV
=> Cửa hàng lỗ:
\(100 \% - 90 \% = 10 \%\) giá trị chiếc TV
=> Số tiền cửa hàng lỗ là:
\(4800000 \times 10 \% = 480000\) (đồng)
Đáp số: 480 000 đồng.
Bài 12. Hình vuông dưới đây được chia làm 4 hình chữ nhật giống hệt nhau và 1 hình vuông nhỏ. Diện tích của mỗi hình chữ nhật là \(140cm^2\), diện tích của hình vuông nhỏ là \(16cm^2\). Tìm chiều rộng của mỗi hình chữ nhật?
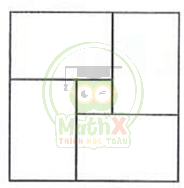
Hướng dẫn:
Ta có diện tích hình vuông nhỏ = \(16cm^2\)
=> Cạnh hình vuông nhỏ = 4cm (vì \(4 \times 4 = 16\))
Ta có diện tích của cả hình vuông to = diện tích của 4 hình chữ nhật + diện tích hình vuông nhỏ
\(= 140 \times 4 + 16 = 576 (cm^2)\)
=> Cạnh của hình vuông to = 24cm (vì \(24 \times 24 = 576\))
Mà như hình vẽ ta thấy được phần độ dài chiều dài lớn hơn chiều rộng chính = độ dài cạnh của hình vuông nhỏ
Tổng chiều dài và chiều rộng chính = độ dài cạnh của hình vuông lớn
=> Chiều rộng hình chữ nhật là:
\((24 - 4) : 2 = 10\) (cm)
Đáp số: 10cm.
Câu 13. Một nhóm học sinh khởi hành từ trại hè vào lúc 8 giờ 45 để đi bộ đến một địa điểm tham quan cách trại hè 24km với vận tốc 4km/h. Ngày hôm sau, họ rời địa điểm đó vào 8 giờ để quay lại trại hè theo đường cũ với vận tốc 5km/h. Khi đi qua một cây cầu nhỏ, họ nhận thấy đúng với thời điểm này của ngày hôm qua, họ đã đi qua nó. Tính thời điểm đó.
Hướng dẫn:
Cách 1:
Giả sử có 2 người cùng đi ở 2 điểm và gặp nhau ở cầu
Người 1 xuất phát ở trại hè lúc 8h45 đi với vận tốc 4km/h
Người 2 xuất phát ở địa điểm tham quan lúc 8h đi với vận tốc 5km/h
Đổi 45 phút = \(\dfrac {3}{4}\) giờ
Ta có đến thời điểm 8 giờ 45 phút người 2 đã đi được quãng đường:
\(\dfrac {3}{4} \times 5 = \dfrac {15}{4}\) (km)
Quãng đường còn lại người 2 phải đi là:
\(24 - \dfrac {15}{4} = \dfrac {81}{4}\) (km)
Lúc này thời gian để 2 người gặp nhau kể từ thời điểm 8 giờ 45 phút là:
\(t = \dfrac {81}{4} :\) Tổng vận tốc của 2 người
\(=> t = \dfrac {81}{4} : (4 + 5) = \dfrac {9}{4}\) (giờ)
Đổi \(\dfrac {9}{4}\) giờ = 2 giờ 15 phút
Vậy thời điểm họ gặp nhau hay chính là ở cây cầu nhỏ là:
8 giờ 45 phút + 2 giờ 15 phút = 11 (giờ)
Cách 2: giải theo cách đại số
Gọi thời điểm gặp nhau là t
Ta có phương trình đại số:
\(4 \times (t – 8,75) + 5 \times (t – 8) = 24 \\ => 4t – 35 + 5t – 40 = 24 \\ => 9t = 24 + 75 \\ => t = 99 : 9 = 11\)
Đáp số: 11 giờ.
Bài 14. Có bao nhiêu số tự nhiên có 6 chữ số mà tổng các chữ số bằng 4
Hướng dẫn:
Số tự nhiên thỏa mãn yêu cầu đề bài có dạng: \(\overline {abcdef}\)
với \(a \neq 0\) và a + b + c+ d + e + f = 4
Trường hợp 1:
4 = 4 + 0 + 0 + 0 + 0 + 0
Có 1 số duy nhất thỏa mãn yêu cầu đề bài là 400000
Trường hợp 2:
4 = 3 + 1 + 0 + 0 + 0 + 0
Nếu a = 3, có 5 cách đặt vị trí chữ số 1: \(\overline {31cdef}; \overline {3b1def}; \overline {3bc1ef}; \overline {3bcd1f}; \overline {3bcde1}\)
Tương tự, nếu a =1, có 5 cách đặt vị trí chữ số 3.
Tổng có 5 + 5 = 10 số thỏa mãn
Trường hợp 3:
4 = 2 + 2 + 0 + 0 + 0 + 0
a = 2, ta có 5 cách đặt vị trí số 2 còn lại
Có 5 số thỏa mãn
Trường hợp 4:
4 = 2 + 1+ 1 + 0 + 0 + 0
- Nếu a = 2, b =1: \(\overline {21cdef}\), ta có 4 cách chọn vị trí đặt chữ số 1 còn lại
Có 4 số thỏa mãn
- Nếu a = 2, c = 1: \(\overline {2b1def}\), ta có 3 cách chọn vị trí đặt chữ số 1 còn lại là d, e, f (không thể chọn vị trí b vì trùng với cách đặt khi a = 2, b = 1)
Có 3 số thỏa mãn
Tương tự:
- Nếu a = 2, d = 1: :\(\overline {2bc1ef}\), ta có 2 cách chọn vị trí đặt chữ số 1 còn lại
Có 2 số thỏa mãn
- Nếu a = 2, e = 1: \(\overline {2bcd1f}\), ta có 1 cách duy nhất để chọn vị trí đặt chữ số 1 còn lại
Có 1 số thỏa mãn
- Nếu a = 1, \(\overline {1bcdef}\),
Ta có 5 cách chọn vị trí cho chữ số 2 (là b, c, d, e, f). Sau khi chọn 1 vị trí bất kỳ cho chữ số 2, ta còn lại 4 vị trí có thể đặt chữ số 1.
Có 5 x 4 = 20 số thỏa mãn
Tổng trường hợp 4 có 4 + 3 + 2 + 1 + 20 = 30 số thỏa mãn đề bài
Trường hợp 5:
4 = 1 + 1 + 1+ 1 + 0 + 0
Trường hợp này ta chỉ có duy nhất 1 cách để chọn a đó là a = 1
Khi a = 1, \(\overline {1bcdef}\), ta cần xếp vị trí cho 2 chữ số 0 và 3 chữ số 1
Trường hợp này tương tự với trường hợp 4 khi a = 2 và ta xếp vị trí cho 2 chữ số 1
Có 10 số thỏa mãn đề bài.
Vậy số các số tự nhiên thỏa mãn đề bài bằng: 1 + 10 + 5 + 30 + 10 = 56 số.
Đáp số: 56 số.
Bài 15. Cho 2023 số tự nhiên sao cho tổng của 5 số bất kỳ trong các số đó là một số lẻ. Có thể khẳng định tổng tất cả 2023 số đã cho đó là một số lẻ được hay không? Giải thích tại sao
Hướng dẫn:
Chia 2023 số tự nhiên đã cho thành các nhóm, mỗi nhóm chứa 5 số bất kỳ
Ta được: 2023 : 5 = 404 nhóm, dư 3 số.
Vì tổng 5 số bất kỳ là 1 số lẻ nên số số chẵn phải nhỏ hơn 5
Suy ra số số lẻ lớn hơn 2018
Xét riêng 3 số lẻ a, b, c. Tổng a + b + c chắc chắn là 1 số lẻ. Còn lại 2020 số chia thành 404 nhóm.
Tổng mỗi nhóm là 1 số lẻ nên tổng 404 là 1 số chẵn.
Vậy tổng 2023 số là 1 số lẻ
Trên đây MATHX đã hướng dẫn giải đề luyện tập toán ôn thi lớp chọn thcs archimedes 2024 - đề 01. Chúc các em học và ôn tập thật tốt
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS ARCHIMEDES ACADEMY được đội ngũ MATHX biên soạn, đầy đủ và chi tiết nhất để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Các em học sinh nếu xem lời giải mà vẫn chưa hiểu thì có thể xem Video thầy Hiếu chữa đề ở phìa bên dưới:
Phụ huynh và các em học sinh xem thêm chủ đề giải đề Archimedes tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG ARCHIMEDES 2020 (BÀI CƠ BẢN)
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG ARCHIMEDES 2020 (BÀI NÂNG CAO)