
Thầy/cô MATHX biên soạn tổng hợp đến các em học sinh đáp án đề thi vào 6 trường THCS Cầu Giấy năm học 2022 2023. Tài liệu gồm đề thi và hướng dẫn giải chi tiết, các em xem đề bài và tự làm bài tập ra vở rồi đối chiếu với đáp án để xem kết quả. Chúc các em ôn tập và làm bài thật tốt trong kì thi vào 6 của mình sắp tới.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 THCS Cầu Giấy qua các năm tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2012 2013
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2013 2014
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2019 2020
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2020 2021
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2021 2022
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2022 2023
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2023-2024
Môn: Toán
Năm học: 2022 - 2023
(đề ghi lại theo trí nhớ của học sinh, có thể có sai số)
Câu 1. Tính: \(3,5\times \dfrac{1}{4}-1,5\times \dfrac{1}{4}\)
A. 0 B. \(\dfrac {1}{2}\) C. \(\dfrac {5}{4}\) D. \(\dfrac {1}{8}\)
Giải
\(3,5\times \dfrac{1}{4}-1,5\times \dfrac{1}{4} \\ = \dfrac{1}{4} \times (3,5 - 1,5) \\ = \dfrac{1}{4} \times 2 \\ = \dfrac{2}{4} \\ = \dfrac{1}{2}\)
Chọn phương án B
Đáp án: B
Câu 2. 0,2m3 gấp 25dm3 số lần là:
A. 0,008 B. 0,8 C. 8 D. 80
Giải
Đổi 0,2m3 = 200dm3
0,2m3 gấp 25dm3 số lần là: 200 : 25 = 8 (lần)
Chọn đáp án C
Đáp án: C
Câu 3. Một ô tô đi với vận tốc 60km/h, tính quãng đường ô tô đi được trong 12 phút.
A. 0,2km B. 5km C. 720km D. 12km
Giải
Đổi 12 phút = 1/5 (giờ)
Quãng đường ô tô đi được trong 12 phút là: 60 x 1/5 = 12 (km)
Chọn đáp án D
Đáp án: D
Câu 4. Một hình hộp chữ nhật có chiều dài là 12cm, chiều rộng là 8cm. Biết hình lập phương có cạnh bằng trung bình cộng ba kích thước của hình hộp chữ nhật và có diện tích toàn phần là 486cm2. Tìm chiều cao của hình hộp chữ nhật.
A. 7cm B. 8cm C. 9cm D. 81cm
Giải
Diện tích một mặt của hình lập phương là: 486 : 6 = 81 (cm2)
Vì 81 = 9 x 9 nên cạnh hình lập phương là 9 (cm)
Tổng ba kích thước của hình hộp chữ nhật là: 9 x 3 = 27 (cm)
Chiều cao hình hộp chữ nhật là: 27 – (12 + 8) = 7 (cm)
Chọn đáp án A
Đáp án: A
Câu 5. Tìm x, biết 15,23 – 5 x = 0,78
Giải
15,23 – 5 x x = 0,78
5 x x = 15,23 – 0,78
5 x x = 14,45
x = 14,45 : 5
x = 2,89
Đáp án: 2,89
Câu 6. Tổng số học sinh khối 5 của một trường tiểu học là một số có ba chữ số và chữ số hàng trăm là 2. Biết khi xếp học sinh thành 10 hàng thì dư 5 học sinh và xếp thành 9 hàng thì không dư. Hỏi số học sinh khối 5 là bao nhiêu?
Giải
Gọi số học sinh của khối 5 là \(\overline {2ab}\) (a, b là các chữ số)
Vì khi xếp học sinh thành 10 hàng thì dư 5 học sinh nên số học sinh là số chia 10 dư 5.
Do đó, số học sinh là \(\overline {2a5}\)
Vì số học sinh khi xếp thành 9 hàng thì không dư nên số học sinh là số chia hết cho 9
→ \(\overline {2a5}\) chia hết cho 9 → (2 + a + 5) chia hết cho 9.
Hay (a + 7) chia hết cho 9 nên a = 2
Vậy khối 5 có 225 học sinh.
Đáp án: 225 học sinh
Câu 7. Tuổi anh bằng \(\dfrac {5}{4}\) tuổi em. Biết hai lần tuổi anh cộng với tuổi em là 28 tuổi. Tính số tuổi của anh.
Giải
Coi tuổi của anh là 5 phần thì tuổi của em là 4 phần.
Khi đó, 2 lần tuổi của anh là 10 phần.
28 tuổi ứng với: 10 + 4 = 14 (phần).
Giá trị một phần là: 28: 14 = 2 (tuổi)
Tuổi của anh là: 2 x 5 = 10 (tuổi).
Đáp án: 10 tuổi
Câu 8. Cho hình thang ABCD có hai đáy AB, CD. Hai đường chéo AC và BD cắt nhau tại O. Biết diện tích tam giác OAD là 11 cm2, diện tích tam giác OAB là 5cm2. Tính diện tích hình thang ABCD.
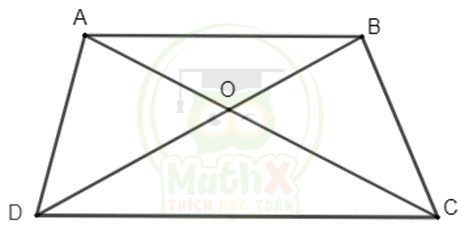
Giải
\({{S}_{ABD}} = {{S}_{AOB}} + {{S}_{AOD}} = 5 + 11 = 16\) (cm2)
\({{S}_{ABD}} = {{S}_{ABC}}\) (chung đáy AB và đường cao hạ từ C xuống AB bằng đường cao hạ từ D xuống AB)
\({{S}_{ABC}} = 16\) (cm2)
\({{S}_{ABC}} = {{S}_{AOB}} + {{S}_{BOC}}\)
\({{S}_{BOC}} = 16 - 5 = 11\) (cm2)
\(\dfrac {OB}{OD} = \dfrac {{{S}_{AOB}}}{{{S}_{AOD}}} = \dfrac {5}{11} = \dfrac {{{S}_{BOC}}}{{{S}_{DOC}}} \)
\({{S}_{DOC}} = 24,2\) (cm2)
Do đó: \({{S}_{ABCD}} = 5 + 11 + 11 + 24,2 = 51,2\) (cm2)
Đáp án: 51,2 cm2
Bài 1 (2 điểm). Một cuộc thi vẽ có 120 học sinh đạt giải. Số học sinh đạt giải nhất bằng 10% tổng số học sinh đạt giải, số học sinh đạt giải nhì bằng \(\dfrac {1}{5}\) tổng số học sinh đạt ba giải còn lại, số học sinh đạt giải ba bằng \(\dfrac {3}{5}\) số học sinh đạt giải khuyến khích.
a) Tính số học sinh đạt giải nhất.
b) Tính số học sinh đạt giải khuyến khích.
Giải
a) Số học sinh đạt giải nhất là: 120 x 10 : 100 = 12 (học sinh)
b) Vì số học sinh đạt giải nhì bằng \(\dfrac {1}{5}\) tổng số học sinh đạt ba giải còn lại nên số học sinh đạt giải nhì bằng \(\dfrac {1}{6}\) tổng số học sinh đạt giải.
Số học sinh đạt giải nhì là: \(120 \times \dfrac {1}{6} = 20\) (học sinh)
Tổng số học sinh đạt giải ba và giải khuyến khích là: 120 - 12 -20 = 88 (học sinh)
Số học sinh đạt giải khuyến khích là: 88 : (3 + 5) x 5 = 55 (học sinh)
Đáp số:
a) 12 học sinh.
b) 55 học sinh.
Bài 2 (1 điểm). Trong kì thi chọn HSG có hai môn thi là Toán và Tiếng Anh. Biết \(\dfrac {1}{10}\) số học sinh giỏi Tiếng Anh bằng \(\dfrac {6}{83}\) số học sinh giỏi Toán. Số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là một số có hai chữ số, chia cho 5 và 9 đều dư 2. Tính số học sinh giỏi Toán, số học sinh giỏi Tiếng Anh.
Giải
Các số có hai chữ số chia cho 5 và 9 đều dư 2 là 47 và 92.
Do đó, số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 47 bạn hoặc 92 bạn.
Vì \(\dfrac {1}{10}\) số học sinh giỏi Tiếng Anh bằng \(\dfrac {6}{83}\) số học sinh giỏi Toán nên \(\dfrac {6}{60}\) số học sinh giỏi Tiếng Anh bằng \(\dfrac {6}{83}\) số học sinh giỏi Toán.
Khi đó, coi số học sinh giỏi Tiếng Anh là 60 phần thì số học sinh giỏi Toán là 83 phần.
Hiệu số phần bằng nhau là: 83 – 60 = 23 (phần)
Vì 47 không chia hết cho 23; 92 chia hết cho 23 nên số học sinh giỏi Toán hơn số học sinh giỏi Tiếng Anh là 92 học sinh.
Số học sinh giỏi Tiếng Anh là 92 học sinh.
Số học sinh giỏi Toán là: 92 : 23 x 83 = 332 (học sinh)
Số học sinh giỏi Tiếng Anh là: 92 : 23 x 60 = 240 (học sinh)
Đáp số:
Số học sinh giỏi Toán: 332 học sinh;
Số học sinh giỏi Tiếng Anh: 240 học sinh
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Cầu Giấy năm học 2022 - 2023
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS CẦU GIẤY để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX