
Thầy/cô MATHX biên soạn tổng hợp đến các em học sinh đáp án đề thi vào 6 trường THCS Cầu Giấy năm học 2019 2020. Tài liệu gồm đề thi và hướng dẫn giải chi tiết, các em xem đề bài và tự làm bài tập ra vở rồi đối chiếu với đáp án để xem kết quả. Chúc các em ôn tập và làm bài thật tốt trong kì thi vào 6 của mình sắp tới.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 THCS Cầu Giấy qua các năm tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2012 2013
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2013 2014
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2019 2020
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2020 2021
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2021 2022
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2022 2023
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2023-2024
Môn: Toán
Năm học: 2019 - 2020
Bài 1. Tìm số tự nhiên x, biết: \(\dfrac{134247}{1000}<134,2x7<\dfrac{134267}{1000}\)
Giải
Ta có: \(\dfrac{134247}{1000}=134,247\)
\(\dfrac{134267}{1000}=134,267\)
Mà: 134,247 < 134,257 < 134,267
-> x = 5
Đáp án: x = 5
Bài 2. Tìm số thứ 7 của dãy 3; 5; 8; 13; 21;…..
Giải
Quy luật: số tiếp theo là tổng của 2 số trước đó, ví dụ số thứ 3 là tổng của số thứ nhất và số thứ 2; số thứ 4 là tổng của số thứ 2 và số thứ 3
Ta có
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
Vậy số thứ 7 của dãy trên là số: 55
Đáp án: 55
Bài 3. Tính giá trị biểu thức: 101 x 34 + 10,1 x 130 - 1,01 x 2700
Giải
101 x 34 + 10,1 x 130 - 1,01 x 2700
= 101 x 34 + 101 x 13 - 101 x 27
= 101 x (34 + 13 - 27)
= 101 x 20
= 2020
Đáp án: 2020
Bài 4. Tìm chữ số tận cùng của dãy sau: 11 x 13 x 15 x 17 x 19 x ... x 2019
Giải
Ta có bất cứ số lẻ nào nhân với 5 đều sẽ ra kết quả là số có chữ số tận cùng là 5
-> Kết quả của dãy phép nhân:
11 x 13 x 15 x 17 x 19 x ... x 2019
Có chữ số tận cùng là 5
Đáp án: 5
Bài 5. Nam có một số bi. Biết nếu xếp mỗi hộp 5 viên bi thì còn dư 3 viên bi. Nếu xếp mỗi hộp 2 hoặc 9 viên bi thì đủ. Hỏi số bi của Nam? Biết Nam có nhiều hơn 110 viên và ít hơn 250 viên.
Giải
Nếu xếp mỗi hộp 5 viên bi thì còn dư 3 viên bi. Nếu xếp mỗi hộp 2 hoặc 9 viên bi thì đủ.
Chứng tỏ số bi của Nam chia hết cho 2 và 9; chia 5 dư 3.
Gọi số bi của Nam là \(\overline {abc}\) (0 < a < 3)
Vì Nam có nhiều hơn 110 viên và ít hơn 250 nên a = 1 hoặc a = 2
Vì số bi chia hết cho 2 và chia 5 dư 3 nên c = 8
TH1: a = 1
-> b = 9
TH2: a = 2
-> b = 8 (loại)
Vậy Nam có số bi là 198 viên bi.
Đáp án: 198 viên bi
Bài 6. Cách đây 4 năm tổng số tuổi 2 chị em là 28 tuổi. Hiện nay tuổi em bằng \(\dfrac {4}{5}\) tuổi chị. Tính tuổi em hiện nay.
Giải
Hiện nay tổng số tuổi 2 chị em là:
28 + 8 = 36 (tuổi)
Số tuổi của em hiện nay là:
36 : (4 + 5) x 4 = 16 (tuổi)
Đáp án: 16 tuổi
Bài 7. Một mảnh đất hình chữ nhật có diện tích là 2020 m2. Nếu tăng chiều dài lên 50% và giảm chiều rộng đi 20% thì diện tích mới là bao nhiêu hecta?
Giải
Diện tích mới là:
2020 x (1,5 x 0,8) = 2424 (m2) = 0,2424 ha.
Đáp án: 0,2424 ha
Bài 8. Cho một số bóng xanh và vàng. Số bóng vàng bằng \(\dfrac {1}{3}\) bóng xanh. Nếu thêm 6 bóng vàng thì bóng vàng bằng \(\dfrac {5}{9}\) bóng xanh. Tính số bóng xanh.
Giải
Số bóng xanh là:
\(6:\left( \dfrac{5}{9}-\dfrac{1}{3} \right)=27\) (bóng xanh)
Đáp án: 27 bóng xanh
Bài 1. Nam dự định đi từ A đến B với vận tốc 40 km/giờ. Đi \(\dfrac {1}{2}\) quãng đường thì Nam nghỉ 15 phút. Để đến B đúng giờ thì Nam phải đi với vận tốc 50 km/giờ. Tính quãng đường AB.
Giải
Xét trên \(\dfrac{1}{2}\) quãng đường còn lại:
Tỉ số vận tốc dự định và vận tốc thực tế là: 40 : 50 = \(\dfrac {4}{5}\)
Trên cùng quãng đường thì thời gian và vận tốc tỉ lệ nghịch nên tỉ số giữa thời gian dự định và thực tế là \(\dfrac{5}{4}\) . Hiệu thời gian là 15 phút.
Thời gian thực tế đi trên \(\dfrac{1}{2}\) quãng đường còn lại là:
15 : (5 - 4) x 4 = 60 (phút) = 1 giờ
Quãng đường AB là:
50 x 1 x 2 = 100 (km).
Đáp số: 100 km
Bài 2. Cho hình tam giác ABC. Lấy M trên AB và N trên AC sao cho
AM = BM và 2 x NC = NA
a, Tính tỉ số diện tích ANM và BMNC
b, Cho MN cắt BC ở D. So sánh BC với CD
Giải
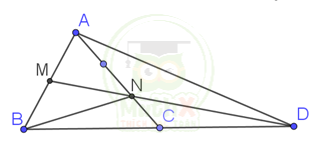
a, Nối N với B ta có:
\({{S}_{AMN}}=\dfrac{1}{2}{{S}_{ANB}}\) (chung chiều cao từ N xuống AB, đáy \(AM=\dfrac{1}{2}AB\) )
\({{S}_{ANB}}=\dfrac{2}{3}{{S}_{ABC}}\) (chung chiều cao từ B xuống AC, đáy \(AN=\dfrac{2}{3}AC\) )
Vậy tỉ số diện tích \(\dfrac{{{S}_{AMN}}}{{{S}_{ABC}}} = \dfrac{1}{2}\times \dfrac{2}{3}=\dfrac{1}{3}\)
Suy ra \(\dfrac{{{S}_{BMNC}}}{{{S}_{ABC}}}=\dfrac{2}{3}\)
\(\Rightarrow \dfrac{{{S}_{AMN}}}{{{S}_{BMNC}}}=\dfrac{1}{2}\)
b, Nối A với D ta có:
\({{S}_{AMD}}={{S}_{BMD}}\) (chung chiều cao từ D xuống AB, đáy AM = NM)
Mà hai tam giác này chung đáy MD nên chiều cao hạ từ A xuống MD bằng chiều cao hạ từ B xuống MD. Từ 2 chiều cao này, kết hợp với việc chung đáy ND nên ta có \({{S}_{AND}}={{S}_{BND}}\)
Lại có \({{S}_{CND}}=\dfrac{1}{2}{{S}_{AND}}\)
(chung chiều cao từ N xuống DB nên đáy \(CD=\dfrac{1}{2}DB\) )
Mà \(BC=\dfrac{1}{2}DB\)
-> BC = CD
Đáp số:
a. \( \dfrac{{{S}_{AMN}}}{{{S}_{BMNC}}}=\dfrac{1}{2}\)
b. BC = CD
Các em học sinh xem Video thầy Trần Hữu Hiếu chữa đề chi tiết bên dưới để hiểu rõ hơn về các bài tập:
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Cầu Giấy năm học 2019 - 2020
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS CẦU GIẤY để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX