
Đội ngũ MATHX gửi đến phụ huynh và các em học sinh đáp án chi tiết cho đề thi tuyển sinh vào lớp 6 THCS Cầu Giấy năm học 2013-2014. Nhằm hỗ trợ các em trong quá trình ôn tập, nâng cao kiến thức và tự tin hơn khi đối mặt với các dạng bài khó. Hy vọng rằng bộ đáp án này sẽ là nguồn tài liệu hữu ích, giúp các em hiểu rõ hơn về cấu trúc đề thi và rèn luyện kỹ năng giải bài tập. Chúc các em thành công và đạt được kết quả xuất sắc trong kỳ thi vào 6 sắp tới!
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 THCS Cầu Giấy qua các năm tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2012 2013
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2013 2014
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2019 2020
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2020 2021
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2021 2022
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2022 2023
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2023-2024
NĂM HỌC 2013 – 2014
Khoanh tròn bằng bút mực đáp án mà bạn cho là đúng trong các đáp án cho trước của mỗi bài tập sau:
Câu 1. Tích sau tận cùng bằng bao nhiêu chữ số 0:
\(A = 34 \times 35 \times 36 \times ... \times 84 \times 85\)
A. 10 B. 11 C. 12 D. 13
Đáp số: D
Câu 2. Nếu 34 học sinh ngồi vào một bàn tròn, khoảng cách ngồi đều nhau thì ai ngồi đối diện với người thứ 6?
A. 17 B. 22 C. 23 D. 24
Đáp số: C
Câu 3. Diện tích phần tô màu trong hình vẽ sau đây là bao nhiêu biết tứ giác ABCD là hình chữ nhật.
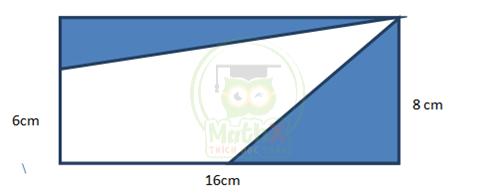
A. 48cm2 B. 80cm2 C. 64cm2 D. 128cm2
Đáp số: A
Câu 4. Diện tích miền tô màu trong hình vẽ sau là bao nhiêu biết trong hình có tứ giác ABCD là hình chữ nhật có nửa đường tròn đường kính AD.
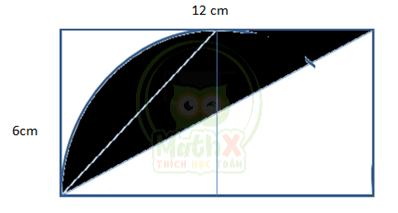
A. 28,26cm2 B. 56,52cm2 C. 7,74cm2 D. 20,52cm2
Đáp số: A
Câu 5. Có bao nhiêu số có 4 chữ số chia hết cho 9 mà trong mỗi số, các chữ số đều khác nhau và đều lẻ?
A. 21 B. 22 C. 24 D. 26
Đáp số: C
Câu 6. Trong phép chia số tạo bởi 500 chữ số 6 cho 15 thì phần thập phân nhận được là bao nhiêu?
A. 1 B. 2 C. 3 D. 4
Đáp số: D
Câu 7. Số tự nhiên a lớn nhất có 3 chữ số biết rằng a chia cho 2 dư 1, a chia cho 5 dư 1, a chia cho 7 dư 3 và a chia hết cho 9 là số nào?
A. 171 B. 981 C. 801 D. 891
Đáp số: C
Câu 8. Một người bố nói với con mình: “10 năm trước đây tuổi của bố gấp 10 lần tuổi của con, 22 năm nữa tuổi của bố sẽ gấp đôi tuổi con”. Hãy tính tuổi bố hiện nay?
A. 40 tuổi B. 50 tuổi C. 54 tuổi D. 72 tuổi
Đáp số: B
Câu 9. Kết quả của phép tính sau là bao nhiêu?
\(M = 7 \times \left( {\dfrac{{191919}}{{212121}} + \dfrac{{888}}{{999}}} \right)\)
A. \(\dfrac{{75}}{9}\) B. \(\dfrac{{75}}{3}\) C. \(\dfrac{{113}}{9}\) D. \(\dfrac{{113}}{3}\)
Đáp số: C
Câu 10. Một chiếc đồng hồ quả lắc cứ đúng 1 giờ trôi qua thì đổ chuông một lần. Số tiếng chuông đổ đúng bằng số giờ mà nó cần điểm báo. Chẳng hạn, khi điểm 1 giờ thì nó đổ một tiếng chuông, khi điểm 2 giờ thì nó đổ hai tiếng chuông. Bạn Hoa thường lắng nghe tiếng chuông, quan sát và tính toán được rằng: Khi đồng hồ điểm 3 giờ thì chuông đổ 3 tiếng, mất tổng cộng 6 giây. Vậy khi đồng hồ điểm 12 giờ thì mất tổng cộng bao nhiêu giây để đổ 12 tiếng chuông?
A. 24 giây B. 36 giây C. 32 giây D. 33 giây
Đáp số: D
Giải các bài tập sau:
Bài 1. (1 điểm)
a) Tính: \(A = \left( {\dfrac{3}{{10}} + \dfrac{4}{5} \times \dfrac{1}{2}} \right):\left( {2\dfrac{8}{9} - 1\dfrac{1}{3}} \right) + 2013\)
b) Tìm x biết: \(1 - \left( {3\dfrac{3}{8} + x - 2\dfrac{5}{{24}}} \right) \times \dfrac{{12}}{{17}} = 0\)
Hướng dẫn:
a) Tính: \(A = \left( {\dfrac{3}{{10}} + \dfrac{4}{5} \times \frac{1}{2}} \right):\left( {2\dfrac{8}{9} - 1\dfrac{1}{3}} \right) + 2013 \)
\(A = \dfrac{7}{{10}}:\dfrac{{14}}{9} + 2013\)
\(A = \dfrac{9}{{20}} + 2013 = 2013\dfrac{9}{{20}}\)
b) Tìm x: \(1 - \left( {3\dfrac{3}{8} + x - 2\dfrac{5}{{24}}} \right) \times \dfrac{{12}}{{17}} = 0\)
\(\left( {3\dfrac{3}{8} + x - 2\dfrac{5}{{24}}} \right) \times \dfrac{{12}}{{17}} = 1 \)
\(\left( {3\dfrac{3}{8} + x - 2\dfrac{5}{{24}}} \right) = \dfrac{{17}}{{12}} \)
\(\dfrac{{27}}{8} + x - \dfrac{{53}}{{24}} = \dfrac{{17}}{{12}}\)
\(\dfrac{{27}}{8} + x = \dfrac{{17}}{{12}} + \dfrac{{53}}{{24}}\)
\(\dfrac{{27}}{8} + x = \dfrac{{87}}{{24}}\)
\(x = \dfrac{{87}}{{24}} - \dfrac{{27}}{8}\)
\(x = \dfrac{1}{4}\)
Bài 2. (1 điểm):
Hai số thập phân có tổng bằng 55,22. Nếu dời dấu phẩy của số bé sang trái 1 hàng rồi lấy hiệu số lớn và nó ta được kết quả là 37,07. Tìm hai số đó.
Hướng dẫn:
Số bé là: \((55,22 - 37,07):11 \times 10 = 16,5\)
Số lớn là: 55,22 – 16,5 = 38,72
Đáp số:
Số bé: 16,5
Số lớn: 38,72
Bài 3. (2 điểm) Cho tứ giác ABCD như hình vẽ có M, N, P, Q lần lượt nằm trên AB, BC, CD, DA sao cho: \(MA = MB;NB = NC;PC = P{\rm{D}};QA = Q{\rm{D}}\) .
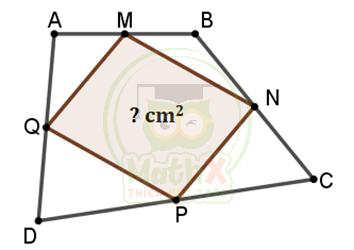
a) Nếu diện tích tứ giác ABCD bằng 90cm2 thì diện tích của tứ giác MNPQ bằng bao nhiêu?
b) Nối CM, AP, BQ, DN và tô màu như hình vẽ. Hãy chứng minh rằng diện tích tứ giác tô màu đỏ bằng tổng diện tích 4 tam giác tô xanh.
Hướng dẫn:
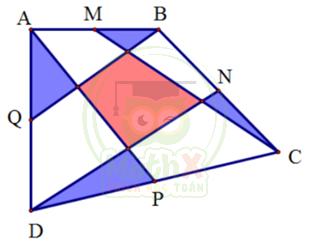
a) Ta có:
\({\dfrac{S_{\mathrm{BMN}}}{S_{\mathrm{BAC}}}}={\dfrac{\mathrm{BM}}{\mathrm{AB}}}\times{\dfrac{\mathrm{BN}}{\mathrm{BC}}}={\dfrac{1}{2}}\times{\dfrac{1}{4}}={\dfrac{1}{4}}\Rightarrow S_{\mathrm{BMN}}={\dfrac{1}{4}}S_{\mathrm{BAC}}\)
\({\dfrac{S_{\mathrm{CNP}}}{S_{\mathrm{CSD}}}}={\dfrac{\mathrm{CN}}{\mathrm{CB}}}\times{\dfrac{\mathrm{CP}}{\mathrm{CD}}}={\dfrac{1}{2}}\times{\dfrac{1}{4}}\to S_{\mathrm{CNP}}={\dfrac{1}{4}}S_{\mathrm{CBD}}\)
\({\dfrac{\mathrm{S}_{\mathrm{DPQ}}}{\mathrm{S}_{\mathrm{DCA}}}}={\dfrac{\mathrm{DP}}{\mathrm{DC}}}\times{\dfrac{\mathrm{DQ}}{\mathrm{DA}}}={\dfrac{1}{2}}\times{\dfrac{1}{4}}\Longrightarrow{\mathrm{S}}_{\mathrm{DPQ}}={\dfrac{1}{4}}{\mathrm{S}}_{\mathrm{DCA}}\)
\(\dfrac{{{S_{AQM}}}}{{{S_{ADB}}}} = \dfrac{{AQ}}{{AD}} \times \dfrac{{AM}}{{AB}} = \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {S_{AMQ}} = \dfrac{1}{4}{S_{ADB}} \)
=> \({S_{MNPQ}} = {S_{ABCD}} - {S_{BMN}} - {S_{CNP}} - {S_{DPQ}} - {S_{AMQ}}\)
=> \({S_{MNPQ}} = {S_{ABCD}} - \dfrac{1}{4}{S_{BAC}} - \dfrac{1}{4}{S_{CBD}} - \dfrac{1}{4}{S_{DCA}} - \dfrac{1}{4}{S_{ADB}} \)
\(\begin{array}{l} {S_{MNPQ}} = {S_{ABCD}} - \dfrac{1}{4} \times \left( {{S_{BAC}} + {S_{DCA}}} \right) - \dfrac{1}{4} \times \left( {{S_{CBD}} + {S_{ADB}}} \right)\\ {S_{MNPQ}} = {S_{ABCD}} - \dfrac{1}{4} \times {S_{ABCD}} - \dfrac{1}{4} \times {S_{ABCD}}\\ {S_{MNPQ}} = \dfrac{1}{2} \times {S_{ABCD}} = \dfrac{1}{2} \times 90 = 45\left( {c{m^2}} \right) \end{array}\)
b)
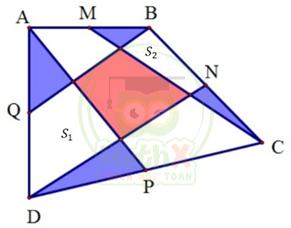
Ta có:
\({S_{xanh}} = {S_{ADP}} - {S_1} + {S_{BCM}} - {S_2}\)
\({S_{xanh}} = \left( {{S_{ADP}} + {S_{BCM}}} \right) - \left( {{S_1} + {S_2}} \right)\)
\({S_{xanh}} = \frac{1}{2}{S_{ABCD}} - \left( {{S_1} + {S_2}} \right)\)
\({S_{do}} = {S_{ABCD}} - {S_{ABQ}} - {S_{DNC}} - {S_1} - {S_2}\)
\({S_{do}} = {S_{ABCD}} - \left( {{S_{ABQ}} + {S_{DNC}}} \right) - \left( {{S_1} + {S_2}} \right) \)
\({S_{do}} = \frac{1}{2}{S_{ABCD}} - \left( {{S_1} + {S_2}} \right) \)
Diện tích phần tô đỏ bằng diện tích phần tô xanh.
Bài 4. (1 điểm) Trong một ngôi đền có 3 vị thần ngồi cạnh nhau. Thần Thật Thà (luôn nói thật), Thần Dối Trá (luôn nói dối) và Thần Khôn Ngoan (lúc nói thật, lúc nói dối). Một nhà toán học hỏi:
Hỏi Thần bên trái: - Ai ngồi cạnh Ngài? Ông ta trả lời: Thần Thật Thà
Hỏi Thần ngồi giữa: - Ngài là ai? Ông ta trả lời: Tôi là Thần Khôn Ngoan.
Hỏi Thần ngồi bên phải: -Ai ngồi cạnh Ngài? Ông ta trả lời: Đấy là Thần dối Trá.
Hãy cùng nhà toán học xác định tên của mỗi vị Thần.
Hướng dẫn:
+ Nếu Thần bên trái là Thần Thật Thà mà ông ta nói thật. Vậy thần ở giữa cũng là Thần Thật Thà (mâu thuẫn)
+ Nếu Thần bên trái là Thần Dối Trá mà ông ta nói dối, suy ra thần ở giữa không phải Thần Thật Thà, vậy thần ở bên tay phải là Thần Thật Thà, mà ông ta nói thật suy ra thần ở giữa là thần Dối Trá (mâu thuẫn).
+ Nếu thần bên tay trái là thần Khôn Ngoan, vậy hai thần còn lại ở hai vị trí còn lại.
+ Nếu thần ở giữa là Thật Thà thì câu trả lời ông ta là Thần khôn Ngoan là mâu thuẫn.
Vậy thần ở giữa là Thần Dối Trá, thần bên tay trái là thần Khôn Ngoan thần bên tay phải là thần Thật Thà.
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Cầu Giấy năm học 2012 - 2013
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS CẦU GIẤY để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.