
Đội ngũ MATHX biên soạn gửi tới các em chọn lọc 99 bài toán ôn thi lớp chọn trường THCS Archimedes 2024. Tài liệu phần 1 gồm 25 câu hỏi đầu kèm lời giải chi tiết. Các em học sinh xem câu hỏi và làm trước sau đó đối chiếu kết quả và cách giải chi tiết trong bài viết này để đạt được hiệu quả ôn tập tốt nhất. Chúc các em học tốt có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm chuỗi 99 bài toán kèm lời giải ôn thi lớp chọn trường Archimedes:
99 BÀI TOÁN KÈM LỜI GIẢI ÔN THI LỚP CHỌN TRƯỜNG ARCHIMEDES (PHẦN 1)
99 BÀI TOÁN KÈM LỜI GIẢI ÔN THI LỚP CHỌN TRƯỜNG ARCHIMEDES (PHẦN 2)
99 BÀI TOÁN KÈM LỜI GIẢI ÔN THI LỚP CHỌN TRƯỜNG ARCHIMEDES (PHẦN 3)
99 BÀI TOÁN KÈM LỜI GIẢI ÔN THI LỚP CHỌN TRƯỜNG ARCHIMEDES (PHẦN 4)
Tài liệu ôn thi lớp 6 chọn trường THCS Archimedes 2024
Bài 1. Bạn có 3 giỏ hoa quả. Giỏ thứ nhất chỉ toàn táo, giỏ thứ hai chỉ toàn cam, giỏ thứ ba lẫn lộn cam và táo. Bạn không nhìn thấy trong mỗi giỏ có loại quả gì. Mỗi giỏ đều có một nhãn hiệu nhưng các nhãn hiệu đều ghi sai. Bạn được phép nhắm mắt thò tay vào một giỏ bất kỳ để lấy ra một quả và mở mắt nhìn quả đó. Làm thế nào có thể xác định được trong mỗi giỏ chứa loại quả nào?
Bài 2. Hai bạn An và Bình chơi bốc bi từ 1 hộp bi theo quy luật như sau: An bốc 1 viên, Bình bốc 2 viên, An bốc 3 viên, Bình bốc 4 viên, An bốc 5 viên, Bình bốc 6 viên, và cứ như vậy...Nếu đến lượt người nào bốc mà không đủ số bi để bốc như quy luật trên thì người đó sẽ bốc tất cả số bi còn lại. Sau khi hết bi trong hộp, An đếm thấy mình bốc được 1012 viên bi. Hỏi lúc đầu trong hộp có tất cả bao nhiêu viên bi?
Bài 3. 1 lớp học có 90 sinh viên:
- 86 em học giỏi Toán.
- 77 em giỏi Lý.
- 72 em giỏi Hóa.
- Số em giỏi Văn ít hơn số em giỏi Hóa 12 người.
- Số em giỏi Tiếng Anh nhiều hơn số em giỏi Văn 6 người.
Hỏi tối thiểu có bao nhiêu sinh viên giỏi cả 5 môn?
Bài 4. Trong một giải bóng đá có k đội tham gia thi đấu vòng tròn 1 lượt (2 đội bất kì thi đấu với nhau một trận). Đội thắng được 3 điểm. Đội hòa được 1 điểm và đội thua không được điểm nào. Kết thúc giải, người ta nhận thấy rằng số trận thắng-thua gấp đôi số trận hòa và tổng số điểm các đội là 176. Hãy tìm k?
Bài 5. Một máy tính thực hiện 6 lệnh như sau:
1) Giá trị ban đầu của X là 3, giá trị ban đầu của S là 0.
2) Tăng X thêm 2.
3) Tăng giá trị của S thêm X đơn vị.
4) Nếu S đạt giá trị tối thiểu là 10000 thì thực hiện lệnh thứ 5. Nếu không trở lại lệnh thứ 2.
5) In ra giá trị của X.
6) Dừng chương trình.
Hỏi máy tính sẽ in ra số nào?
Bài 6. Thu, Thảo, Tuấn, mỗi bạn có một tấm bìa, trên đó có ghi một số tự nhiên. Không ai biết số trên tấm bìa của hai bạn còn lại. Sau khi được biết rằng ba số trên tấm bìa là khác nhau, có tổng bằng 13 và tích là một số lẻ. Thu và Thảo đoán ngay ra tích của ba số đo nhưng Tuấn không đủ thông tin để đoán được. Hỏi trên tấm bìa của Tuấn ghi số mấy?
Bài 7. Trong hộp có 30 viên bi đỏ, 20 viên bi xanh, 10 viên bi vàng, 8 viên bị trắng và 4 viên bi đen. Hỏi Trung cần lấy ít nhất bao nhiêu viên bi trong hộp để chắc chắn có được 2 màu, mỗi màu có ít nhất 5 viên bi?
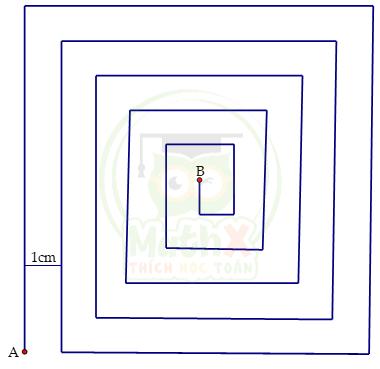
Bài 8. Một con kiến con di chuyển từ A đến B, theo đường gấp khúc cho trong hình dưới đây. Biết rằng, khoảng cách giữa hai đường thẳng song song cạnh nhau là 1cm. Hỏi đường đi của con kiến dài bao nhiêu cm?
Bài 9. Có 6 cái hộp được đánh số từ 1 đến 6. Bạn Hồng bỏ 2018 tấm thẻ được đánh số từ 1 đến 2018 vào các hộp như sau: thẻ số 1 vào hộp 1; thẻ số 2 vào hộp 2;…. ; thẻ số 6 vào hộp 6, sau đó, thẻ số 7 vào hộp 5; thẻ số 8 vào hộp 4; … Hồng tiếp tục làm như vậy cho đến khi hết thẻ. Hỏi thẻ số 2018 được bỏ vào hộp nào?
Bài 10. Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số chẵn có 3 chữ số và các chữ số đôi một khác nhau?
Bài 11. Có hai bình nước I và II. Nếu rót \(\dfrac {1} {3}\) lượng nước ở bình I sang bình II, rồi sau đó lại rót 10 lít từ bình II sang bình I, thì lượng nước ở bình I gấp đôi lượng nước ở bình II. Hỏi ban đầu bình II có bao nhiêu lít nước?
Bài 12. Trong một giải bóng đá tứ hùng, bốn đội M, Y, T, S thi đấu vòng tròn một lượt. Đội thắng được 3 điểm, đội thua được 0 điểm, nếu hai đội hòa nhau thì mỗi đội được 1 điểm. Kết thúc giải, đội M có không ít điểm hơn đội T, hiệu số bàn thắng – bàn thua của đội T là 4 – 1, hiệu số bàn thắng – bàn thua của đội M là 1 – 4. Hỏi các trận đấu mà đội M đã chơi có những tỉ số nào? Các trận đấu mà đội T đã chơi có những tỉ số nào?
Bài 13. Bạn Dương có 3 đống sỏi với số viên sỏi lần lượt là 10; 20; 60. Dương chơi trò chuyển sỏi theo qui tắc sau: Ở mỗi lượt chơi, Dương lấy 2 viên sỏi từ hai đống, mỗi đống 1 viên, rồi chuyển vào đống còn lại.
a) Hà đứng nhìn và thấy Dương đã 3 lần chuyển sỏi vào đống số 1, 4 lần chuyển sỏi vào đống số 2 và 3 lần chuyển sỏi vào đống số 3. Hỏi sau 10 lượt chơi đó, số sỏi ở mỗi đống là bao nhiêu?
b) Hỏi với 3 đống sỏi ban đầu, sau một số lượt chơi theo qui tắc nêu trên, Dương có thể thu được 3 đống sỏi với số sỏi bằng nhau hay không? Vì sao?
Bài 14. Tính giá trị của biểu thức:
\(A = \dfrac{{20192019}}{{2019}} \times \dfrac{{2018}}{{20182018}} \times \dfrac{{20172017}}{{2017}} \times \dfrac{{2016}}{{20162016}} \times ... \times \dfrac{{2002}}{{20022002}} \times \dfrac{{20012001}}{{2001}}. \)
Bài 15. Dùng bốn chữ số 0, 1, 2, 9 có thể lập được bao nhiêu số nhỏ hơn 2019, chia hết cho 3, và trong mỗi số đó, mỗi chữ số chỉ có mặt tối đa một lần?
Bài 16. Vào lúc 8 giờ 5 phút sáng, trên mặt đồng hồ điện tử hiện thị 08 : 05. Vào lúc 8 giờ 19 phút tối, trên mặt đồng hồ điện tử hiển thị 20 : 19. Bây giờ, trên mặt đồng hồ đang hiển thị 21 : 09. Hỏi sau ít nhất bao nhiêu phút nữa, trên mặt đồng hồ điện tử sẽ lại hiển thị đủ bốn chữ số 2, 0, 1, 9?
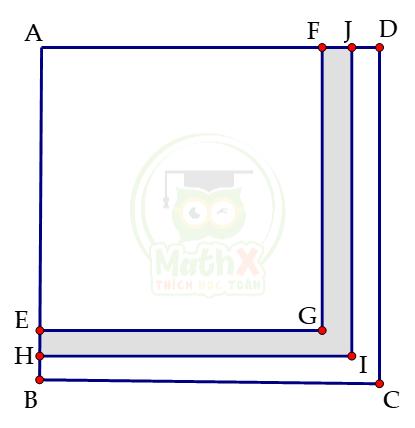
Bài 17. Trong hình dưới đây, ABCD, AHIJ và AEGF là các hình vuông; H là trung điểm đoạn thẳng BE. Độ dài các cạnh của các hình vuông nói trên, theo đơn vị cm, đều là các số tự nhiên. Hãy tính độ dài đoạn thẳng AB, biết rằng diện tích phần được tô đậm bằng 19cm2
Bài 18. Một quầy hàng bán bút có chương trình khuyến mãi sau: mua 4 tặng 1, mua 6 tặng 2 và tặng thêm 1000 đồng. Hỏi để mua đúng 38 cây bút ở quầy hàng đó, người mua cần có ít nhất bao nhiêu tiền? Biết rằng, mỗi cây bút có giá 2000 đồng?
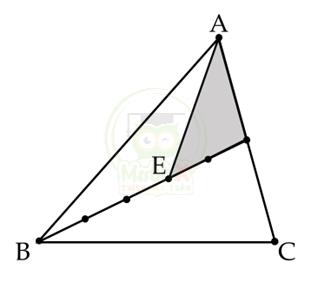
Bài 19. Trong hình vẽ bên dưới, D là điểm nằm trên cạnh AC của tam giác ABC và AD = DC; E là điểm trên đoạn BD thảo mãn BE : BD = 3 : 5. Biết rằng diện tích tam giác ADE là 96cm2. Tính diện tích tam giác ABC.
Bài 20. Nam có bốn quyển sách gồm Toán, Tiếng Việt, Tiếng Anh và Lịch Sử. Nam muốn xếp bốn quyển sách này lên một kệ sách trống sao cho quyển sách Toán và quyển sách Lịch Sử không nằm cạnh nhau. Hỏi, có bao nhiêu cách xếp?
Bài 21. Trong một cuộc thi, có năm thí sinh tham dự A, B, C, D và E. Trước khi cuộc thi diễn ra, có bốn dự đoán về kết quả xếp hạng của năm thí sinh như sau:
Kết thúc cuộc thi, người ta nhận thấy rằng mỗi dự đoán đều đúng cho một thí sinh nào đó và sai cho người còn lại. Biết rằng không có hai thí sinh nào có cùng thứ hạng, hỏi ai đứng thứ ba ở cuộc thi đó?
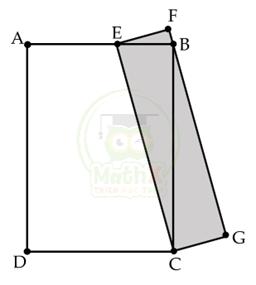
Bài 22. Trong hình vẽ bên dưới, ABCD và CEFG là hai hình chữ nhật, trong đó điểm B nằm trên cạnh FG của hình chữ nhật CEFG và điểm E nằm trên cạnh AB của hình chữ nhật ABCD thỏa mãn AE : EB = 3 : 2. Biết rằng diện tích hình chữ nhật ABCD là 35cm2. Tính diện tích hình chữ nhật CEFG.
Bài 23. Cho 16 số tự nhiên phân biệt khác 0 thỏa mãn tích của năm số bất kỳ trong 16 số này là số chẵn. Gọi S là tổng của 16 số này. Biết rằng S là số lẻ, hỏi S có thể nhận giá trị nhỏ nhất là bao nhiêu?
Bài 24. Cho số A = 206920692069…2069 (A gồm 250 số 2069 viết liền nhau). Người ta muốn xóa một chữ số của số A sao cho số thu được có tổng tất cả các chữ số bằng 2021. Hỏi, có thể xóa được nhiều nhất bao nhiêu chữ số? Khi đó, số lớn nhất có thể thu được là bao nhiêu?
Bài 25. Minh đọc cuốn sách trong 4 ngày. Ngày thứ nhất đọc được 20% số trang sách và thêm 5 trang. Ngày thứ 2 đọc được 60% số trang sách còn lại và 30 trang. Ngày thứ 3 đọc được 50% số trang còn lại và 50 trang. Ngày thứ 4 đọc được 30 trang. Hỏi cuốn sách đó bao nhiêu trang?
Các bài toán trong đề thi vào lớp 6 chọn trường Archimedes nói chung đều ở mức độ khó. Để nâng cao kỹ năng giải bài ngoài việc học trên lớp, các em nên tham khảo thêm một số tài liệu bổ trợ và làm bài tập phần đề thi năm trước. Ngoài ra các em có thể tham khảo các chuyên đề và tài liệu trong ÔN THI THCS ARCHIMEDES ACADEMY để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.