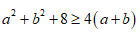CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 1. Phương pháp xét hiệu và biến đổi tương đương
Ví dụ: Cho a > b. Chứng minh rằng: a3 > b3
Bài 2. Phương pháp xét hiệu và biến đổi tương đương (tiếp)
Ví dụ: Chứng minh rằng .png)
Bài 3. Phương pháp xét hiệu và biến đổi tương đương (tiếp theo)
Ví dụ: Chứng minh rằng:
.png)
Bài 4. Phương pháp xét hiệu và biến đổi tương đương (tiếp theo)
Chứng minh rằng:
.png)
Ví dụ: Chứng minh rằng:
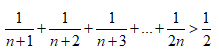
Ví dụ: Chứng minh rằng:
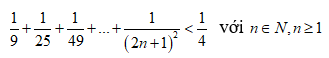
Ví dụ: Cho 3 số a, b, c thỏa mãn a + b +c > 0, ab + bc + ca > 0, abc > 0. Chứng minh rằng: a > 0, b > 0, c > 0.
Bài tập về nhà bài học: Bài 7. Phương pháp phản chứng
Học sinh làm bài tập về nhà ra vở riêng một cách chăm chỉ và cẩn thận, sau đó download file đáp án để so đáp án và sửa lại các bài sai.
Chúc các em làm bài tốt !
Ví dụ: Cho 0 < a, b ,c < 1. Chứng minh rằng có ít nhất một trong các bất đẳng thức sau đây là sai.
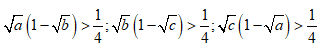

Ví dụ: Chứng minh rằng: