
Thầy/cô MATHX biên soạn đến các em học sinh đáp án đề thi tuyển sinh vào 6 trường THCS Cầu Giấy năm từ 2012 - 2013. Tài liệu gồm đề thi và hướng dẫn giải chi tiết, các em xem đề bài và tự làm bài tập ra vở rồi đối chiếu với đáp án để xem kết quả. Chúc các em ôn tập và làm bài thật tốt trong kì thi vào 6 của mình sắp tới.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 THCS Cầu Giấy qua các năm tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2012 2013
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2013 2014
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2019 2020
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2020 2021
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2021 2022
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2022 2023
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2023-2024
NĂM HỌC: 2012-2013
Khoanh tròn bằng bút mực đáp án mà bạn cho là đúng trong các đáp án cho trước của mỗi bài tập sau:
Câu 1. Cho các phân số: \(x = \dfrac{7}{8};{\rm{ }}y = \dfrac{{66}}{{77}};{\rm{ }}t = \dfrac{{4444}}{{5555}};{\rm{ }}m = \dfrac{{33333}}{{44444}}\)
Số nhỏ nhất trong 4 số trên là:
A. x B. y C. m D. t
Đáp án: C
Câu 2. Đổi 5kg3g ra đơn vị kg ta được kết quả là:
A. 5,3kg B. 5,003kg C. 5,03kg D. 5,0003kg
Đáp án: B
Câu 3. Khi viết dãy số 1, 2, 3,….., 100 thì bạn An đã dùng số chữ số là:
A. 189 B. 190 C. 192 D. 194
Đáp án: C
Câu 4. Một ôtô đi từ A đến B trong một thời gian dự định. Nếu đi với vận tốc 45km/giờ thì đến B chậm 30 phút so với dự định. Nếu đi với vận tốc 60km/giờ thì lại đến B sớm 30 phút. Hỏi nếu đi với vận tốc 50km/giờ thì ôtô đó đi hết quãng đường AB trong thời gian bao lâu?
A. 3 giờ B. 3,5 giờ C. 3,6 giờ D. 4 giờ
Đáp án: C
Câu 5. Số tự nhiên a có 2 chữ số, khi viết thêm số 21 vào đằng trước số a thì ta được một số gấp 31 lần số a. Vậy số a có tổng các chữ số là:
A. 70 B. 7 C. 10 D. 8
Đáp án: B
Câu 6. Có 20 người đứng thành vòng tròn, tất cả đều quay mặt vào tâm, các vị trí đứng được đánh số thứ tự từ 1 đến 20 theo chiều kim đồng hồ. Họ đọc các số tự nhiên từ 1, 2, 3…. Theo chiều kim đồng hồ như sau:
Người đứng ở vị trí thứ nhất đọc số 1
Người đứng ở vị trí thứ hai đọc số 2
Người đứng ở vị trí thứ ba đọc số 3,…
Người kế tiếp đọc số tự nhiên lớn hơn 1 đơn vị so với số mình vừa nghe của người bên cạnh đọc.
Hỏi người đứng ở vị trí bao nhiêu sẽ đọc số 2012?
A. 10 B. 11 C. 12 D. 16
Đáp án: C
Câu 7. Một công nhân làm việc trong một tuần (gồm 6 ngày vì chủ nhật nghỉ).
Ngày thứ nhất ông ta được lĩnh 2 đôla
Ngày thứ hai ông ta được lĩnh 4 đôla
Cứ như vậy ngày sau ông được lĩnh gấp đôi ngày trước.
Hỏi tiền công ông ta được lĩnh trong một tuần là bao nhiêu đôla?
A. 30 B. 122 C. 124 D. 126
Đáp án: D
Câu 8. Một nông dân mua 749 con cừu. Ông ta bán 700 con với số tiền ông ta đã mua 749 con. Với 49 con còn lại, ông ta cũng bán mỗi con với giá như đã bán 700 con. Hỏi phần trăm tiền lãi tính trên vốn ông ta bỏ ra được bao nhiêu?
A. 6,5% B. 7% C. 7,5% D. 8%
Đáp án: B
Câu 9. Có bao nhiêu số tự nhiên khác 0 và nhỏ hơn 1000 mà không chia hết cho 5, không chia hết cho 7?
A. 688 B. 686 C. 684 D. 658
Đáp án: B
Câu 10. Có 6 túi bi chứa lần lượt 18, 19, 21, 23, 25 và 34 viên bi. Chỉ có một túi là chứa toàn những viên bi trầy xước, còn 5 túi kia không chứa viên bi nào trầy xước cả. Lan lấy 3 túi, còn Minh lấy 2 túi, để lại túi chỉ gồm những viên bi trầy xước. Nếu số bi của Lan gấp đôi số bi của Minh thì hỏi có bao nhiêu viên bi trầy xước tất cả?
A. 18 B. 19 C. 21 D. 23
Đáp án: D
Giải các bài tập sau:
Bài 1. (1 điểm) Tính: \(A = \dfrac{1}{6} \times \left( {1\dfrac{1}{2} - \dfrac{3}{4}} \right) + 0,25 \)
Hướng dẫn:
\(A = \dfrac{1}{6} \times \left( {\dfrac{3}{2} - \dfrac{3}{4}} \right) + 0,25 = \dfrac{1}{6} \times \frac{3}{4} + 0,25 = \dfrac{1}{8} + \dfrac{1}{4} = \dfrac{3}{8} \)
Bài 2. (1 điểm) Tìm x biết: \(\dfrac{{1313}}{{1212}}:x = \dfrac{1}{{1 \times 2}} + \dfrac{1}{{2 \times 3}} + \dfrac{1}{{3 \times 4}} + \dfrac{1}{{4 \times 5}} + \dfrac{1}{{5 \times 6}}\ \)
Hướng dẫn:
\(\dfrac{{1313}}{{1212}}:x = \dfrac{1}{{1 \times 2}} + \dfrac{1}{{2 \times 3}} + \dfrac{1}{{3 \times 4}} + \dfrac{1}{{4 \times 5}} + \dfrac{1}{{5 \times 6}}\ \)
\(\dfrac{{13}}{{12}}:x = 1 - \dfrac{1}{6} \)
\(x = \dfrac{{13}}{{12}}:\dfrac{5}{6} = \dfrac{{13}}{{10}}\)
Đáp số: \(\dfrac{{13}}{{10}}\)
Bài 3. (1,5 điểm) Trong hình vẽ sau cho tam giác ABC có diện tích là 100cm2. Trên AC lấy F sao cho AF = \(\dfrac{{1}}{{3}}\) AC. Lấy G là trung điểm của BF. Nối AG cắt BC tại E.
a) Tính diện tích tam giác ABF.
b) Tính tỷ số \(\dfrac{{BE}}{{BC}}\) .
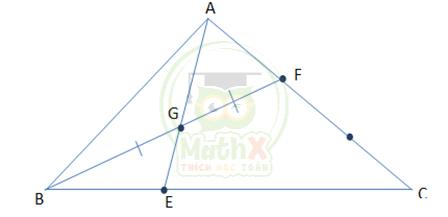
Hướng dẫn:

a) Ta có: \({S_{ABF}} = \dfrac{1}{3} \times {S_{ABC}} \) (Vì 2 tam giác có chung đường cao hạ từ đỉnh B xuống AC và \({\rm{AF}} = \dfrac{1}{3} \times AC\))
Vậy \({S_{ABF}} = \dfrac{1}{3} \times 100 = \dfrac{{100}}{3}c{m^2} \)
b) Nối G với C.
Ta có \({S_{ABG}} = {S_{AGF}}\) (Vì 2 tam giác có chung chiều cao hạ từ A xuống đáy BF và BG=GF)
Mà \({S_{AGF}} = \dfrac{1}{3} \times {S_{CGA}}\) (Vì 2 tam giác có chung đường cao hạ từ G xuống đáy AC và \({\rm{AF}} = \dfrac{1}{3} \times AC\))
Suy ra \({S_{ABG}} = \dfrac{1}{3} \times {S_{CGA}}\)
Mà hai tam giác này có chung cạnh GA suy ra đường cao hạ từ B xuống AG = \(\dfrac{{1}}{{3}}\) đường cao hạ từ C xuống AG.
Suy ra \({S_{BGE}} = \dfrac{1}{3} \times {S_{CGE}}\)
Hai tam giác này có chung đường cao hạ từ C xuống BC, suy ra \({\rm{BE}} = \dfrac{1}{3} \times EC\)
Vậy \({\rm{BE}} = \dfrac{1}{4} \times EC\)
Bài 4. (1 điểm) Cho bảng vuông như hình dưới đây là hình vuông kỳ diệu, có nghĩa là tổng 3 số trong mỗi hàng, mỗi cột, mỗi đường chéo chính đều bằng nhau. Tìm giá trị của số x ở góc trên cùng bên trái.
| x | 21 | 94 |
| 3 | ||
Hướng dẫn:
| x | 21 | 94 |
| 3 | ||
Theo bài ta có tổng của 3 ô là: x + 21 + 94 = x + 115.
Vậy trong ô vuông ở hàng thứ 3 cột bên trái có giá trị: 112
Suy ra ô vuông ở giữa có giá trị: x – 91
| x | 21 | 94 |
| 3 | x - 91 | |
| 112 |
Ta có ô vuông hàng thứ hai cột bên phải là: 203
Suy ra ô vuông ở hàng thứ ba cột bên phải là: x – 182
| x | 21 | 94 |
| 3 | x - 91 | 203 |
| 112 | x - 182 |
Vậy ta có:
x + x - 91 + x - 182 = x + 115
\(x \times 2 = 388\)
x = 194
Đáp số: 194
Bài 5. (0,5 điểm) Tìm số có 5 chữ số \(\overline {abcde} \). Biết \(\overline {abcde} = a \times b \times c \times d \times e \times 45 \)
Hướng dẫn:
Các chữ số a, b, c, d, e phải lẻ vì nếu một trong các chữ số mà chẵn thì tích trên có chữ số tận cùng là 0 hay 2 = 0.
Suy ra tích = 0 hay \(\overline {abcde} \) = 0 (vô lý)
Ta có \(\overline {abcde} \) chia hết cho 45 suy ra \(\overline {abcde} \) chia hết cho 5 và 9
Ta có \(\overline {abcde} \) chia hết cho 45 suy ra \(\overline {abcde} \) chia hết cho 5 suy ra e = 5
Với e = 5 thì \(\overline {abcde} \) chia hết cho 25, suy ra d =7 ( vì 75 chia hết cho 25)
Ta có: \(\overline {abcde} = a \times b \times c \times d \times e \times 45 \)
\(\overline {abcde} = a \times b \times c \times 1575\)
\(\overline {abcde} \) lớn nhất là 99999 suy ra \(a \times b \times c < 99999:1575\) hay a x b x c bé hơn 63.
Để \(\overline {abcde} \) chia hết cho 9 thì (a+ b + c + 7 + 5) chia hết cho 9
Hay (a + b + c + 12) chia hết cho 9.
Mà 12 chia cho 9 dư 3, suy ra (a+b+c) chia cho 9 dư 6
a, b, c đều lẻ suy ra a + b + c cũng lẻ và chia 9 dư 6. Suy ra a + b + c = 15.
Suy ra 3 chữ số có tổng là 15 là:
1 + 7 + 7
1 + 5 + 9
3 + 5 + 7 ( loại vì tích 3 số lớn hơn 63)
3 + 3 + 9 ( loại vì tích 3 số lớn hơn 63)
5 + 5 + 5 ( loại vì tích 3 số lớn hơn 63)
Ta thử chọn hai trường hợp đầu tiên:
\(\overline {abcde} = 1 \times 7 \times 7 \times 7 \times 5 \times 45 = 77175 \)
\(\overline {abcde} = 1 \times 5 \times 9 \times 7 \times 5 \times 45 = 70875 \)
Vậy số \(\overline {abcde} \) là 77175.
Đáp số: 77175
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Cầu Giấy năm học 2012 - 2013
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS CẦU GIẤY để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX