
Thầy/cô MATHX xin gửi đến các em bản đáp án chính thức của đề thi tuyển sinh vào lớp 6 THCS Cầu Giấy năm học 2020-2021. Để giúp các em đánh giá kết quả cá nhân, nâng cao kiến thức và chuẩn bị tốt nhất cho các kì thi sắp tới, MATHX hy vọng rằng đây sẽ là nguồn tư liệu hữu ích và giúp các em trong quá trình ôn tập. Chúc các em học tốt và thành công trong kì thi vào 6 sắp tới.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 THCS Cầu Giấy qua các năm tại đây:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2012 2013
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2013 2014
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2019 2020
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2020 2021
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2021 2022
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2022 2023
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS CẦU GIẤY 2023-2024
NĂM HỌC 2020 – 2021
Câu 1. \(13,28 \times 9,9 + 13,28 \times 0,1 = ?\)
Hướng dẫn:
\(\begin{array}{l} 13,28 \times 9,9 + 13,28 \times 0,1\\ = 13,28 \times \left( {9,9 + 0,1} \right)\\ = 13,28 \times 10\\ = 132,8 \end{array} \)
Đáp số: 132,8
Câu 2. Hùng và Cường hẹn nhau lúc 8 giờ 40 phút. Hùng đến lúc 8 giờ 20 phút. Cường đến muộn 12 phút. Hỏi Hùng phải đợi Cường bao nhiêu lâu?
Hướng dẫn:
Hùng đến sớm hơn 20 phút.
Cường đến muộn 12 phút.
Hùng phải đợi Cường 20 + 12 = 32 (phút)
Đáp số: 32 phút
Câu 3. 32% của một số là 6,4. Vậy \(\dfrac{5}{8}\) của số đó là bao nhiêu?
Hướng dẫn:
6,4 tương đương 32%. Vậy 100% tương đương với \(\dfrac{{100 \times 6,4}}{{32}} = 20\)
Vậy \(\dfrac{5}{8}\) của số đó là: \(\dfrac{5}{8}\).x 20 = 12,5
Đáp số: 12,5
Câu 4. Cho 1 hình lập phương có diện tích toàn phần lớn hơn diện tích xung quanh là 72cm2 Tính thể tích hình lập phương đó?
Đáp số:
Diện tích toàn phần gồm 6 mặt, diện tích xung quanh gồm 4 mặt.
Diện tích 1 mặt hình lập phương là:
72 : 2 = 36 (cm2)
Ta có 36 = 6 × 6 nên độ dài cạnh hình lập phương là 6 (cm)
Thể tích hình lập phương đó là: 6 × 6 × 6 = 216 (cm3)
Đáp số: 216cm3
Câu 5. Lớp 5A có 50 học sinh. 50% bạn thích đá bóng, 12% thích chạy, 18% thích đá cầu. Số còn lại thích chơi cầu lông. Hỏi số bạn thích chơi cầu lông là bao nhiêu?
Hướng dẫn:
Số học sinh thích đá bóng là: 50 x 50 : 100 = 25 (bạn)
Số học sinh thích chạy là: 12 x 50 : 100 = 6 (bạn)
Số học sinh thích đá cầu là: 18 x 50 : 100 = 9 (bạn)
Số học sinh thích chơi cầu lông là: 50 – (25 + 6 + 9) = 10 (bạn)
Đáp số: 10 bạn
Câu 6. Hai số có hiệu là 1554. Tổng của 2 số là \(\overline {2x3y} \) chia hết cho 2, 5 và 9. Hỏi số lớn là số nào?
Hướng dẫn:
\(\overline {2x3y} \) chia hết cho 2, 5 và 9 nên y = 0 và x = 4
Số lớn là: (2430 + 1554) : 2 = 1992
Đáp số: 1992
Câu 7. Lúc 14 giờ một xe đi từ A đến B với vận tốc là 30km/giờ. Đến 14 giờ 45 phút, xe đó nghỉ 15 phút. Sau đó xe đó đi nốt quãng đường với vận tốc là 40km/giờ. Đến 16 giờ 12 phút thì xe tới B. Tính độ dài quãng đường AB.
Hướng dẫn:
Thời gian xe đi với vận tốc 30km/giờ là:
14 giờ 45 phút – 14 giờ = 45 phút = 0,75 (giờ)
Quãng đường lúc đầu xe đi được là: 30 × 0,75 = 22,5 (km)
Thời gian sau khi nghỉ 15phút là: 14 giờ 45 phút + 15 phút = 15 giờ
Thời gian đi quãng đường còn lại là 16h 12 phút - 15h = 1 giờ 12 phút = 1,2 (giờ)
Quãng đường đi với vận tốc 40km/giờ là: 40 × 1,2 = 48 (km)
Độ dài quãng đường AB là: 22,5 + 48 = 70,5 (km)
Đáp số: AB = 70,5km
Câu 8. Cho hình vẽ, biết \({S_{KQBC}} = 26c{m^2} \) và \(\dfrac{{BQ}}{{AB}} = \dfrac{1}{6};\dfrac{{AK}}{{AC}} = \dfrac{1}{3}\) Tính \({S_{AKQ}}\)
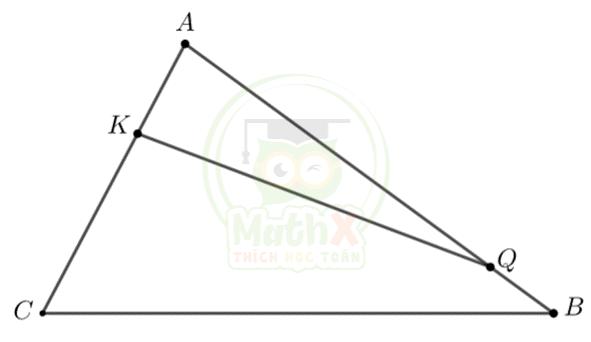
Hướng dẫn:
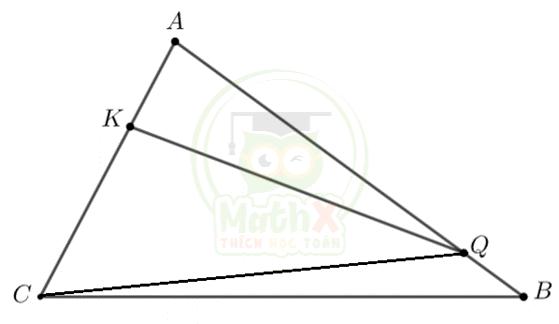
Tam giác QAK và tam giác QAC có chung đường cao hạ từ đỉnh Q và \(\dfrac{{AK}}{{AC}} = \dfrac{1}{3}\) nên \(\dfrac{{{S_{QAK}}}}{{{S_{QAC}}}} = \dfrac{1}{3}\) (1)
\(\dfrac{{BQ}}{{AB}} = \dfrac{1}{6} \Rightarrow \dfrac{{AQ}}{{AB}} = \dfrac{5}{6}\).
Tam giác CAQ và tam giác CAB có chung đường cao hạ từ đỉnh C và đáy \(\dfrac{{AQ}}{{AB}} = \dfrac{5}{6}\) nên \(\dfrac{{{S_{CAQ}}}}{{{S_{CAB}}}} = \dfrac{5}{6}\) (2)
Từ (1) và (2) ta có: \(\dfrac{{{S_{QAK}}}}{{{S_{QAC}}}} \times \dfrac{{{S_{CAQ}}}}{{{S_{CAB}}}} = \dfrac{1}{3} \times \dfrac{5}{6}\)
Suy ra \(\dfrac{{{S_{QAK}}}}{{{S_{CAB}}}} = \dfrac{5}{{18}}\) hay \(\dfrac{{{S_{QAK}}}}{{{S_{KQBC}}}} = \dfrac{5}{{13}}\)
Vậy \({S_{AKQ}} = 26:13 \times 5 = 10\) (cm2)
Đáp số: 10cm2
Câu 1. Cho kệ sách có 3 tầng với 700 quyển sách. 40% số sách ở tầng 1.
a) Tính số sách ở tầng 1.
b) Nếu chuyển nửa số sách từ tầng 3 sang tầng 2 thì số sách tầng 3 bằng \(\dfrac{2}{5}\) số sách ở tầng 2. Tính số sách mỗi tầng ban đầu.
Hướng dẫn:
a) Số sách ở tầng 1 là: 700 × 40 : 100 = 280 (quyển)
b) Tổng số sách ở tầng 2 và tầng 3 là: 700 – 280 = 420 (quyển)
Nếu chuyển nửa số sách từ tầng 3 sang tầng 2 thì tổng số sách 2 tầng này không đổi.
Số sách tầng 3 lúc sau là: 420 : (2 + 5) × 2 = 120 (quyển)
Số sách tầng 3 lúc đầu là: 120 × 2 = 240 (quyển)
Số sách tầng 2 lúc đầu là: 420 – 240 = 180 (quyển)
Đáp số:
a) Tầng 1: 280 quyển
b) Tầng 2: 180 quyển
Tầng 3: 240 quyển
Câu 2. Nam viết lên bảng 3 số 1, 2, 3. Nam xóa đi 2 số a, b, và thay bằng 1 số là \(c = \dfrac{{a \times b}}{{a + b}} \) Nam xóa cho đến khi chỉ còn 1 số.
a) Hỏi số đó là số nào? Vì sao?
b) Nam cũng chơi trò chơi đó, nhưng có 5 số 1, 2, 3, 4, 5. Xong Nam nhận xét lần chơi nào cũng ra số cuối cùng giống nhau. Hỏi Nam nhận xét đúng hay sai? Vì sao?
Hướng dẫn:
a) Nếu Nam xóa đi số 1 và 2 thì sẽ thay bằng số \(\dfrac{{1 \times 2}}{{1 + 2}} = \dfrac{2}{3}\).
Sau đó xóa số \(\dfrac{2}{3}\) và 3 thì sẽ thay bằng số \(\dfrac{{\dfrac{2}{3} \times 3}}{{\dfrac{2}{3} + 3}} = 2:\dfrac{{11}}{3} = 2 \times \dfrac{3}{{11}} = \dfrac{6}{{11}} \).
Tương tự với 2 trường hợp còn lại xóa đi 1 và 3 hay 2 và 3 thì cũng ra được kết quả \(\dfrac{6}{{11}} \).
Vậy số Nam thu được luôn là số \(\dfrac{6}{{11}} \)
b) \(c = \dfrac{{a \times b}}{{a + b}} \). Suy ra \(\dfrac{1}{c} = \dfrac{{a + b}}{{a \times b}} = \dfrac{a}{{a \times b}} + \dfrac{b}{{a \times b}} = \dfrac{1}{b} + \dfrac{1}{a}\).
Gọi số cuối cùng là d thì \(\dfrac{1}{d} = \frac{1}{1} + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} = \dfrac{{137}}{{60}}\)
Suy ra \(d = \dfrac{{60}}{{137}}\)
Vậy Nam nhận xét đúng, số cuối cùng luôn là \(\dfrac{{60}}{{137}}\).
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Cầu Giấy năm học 2020 - 2021.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS CẦU GIẤY để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.