
Thầy Trần Hữu Hiếu biên soạn gửi các em học sinh 8 cách giải khác nhau cho bài toán hình học đề thi vào lớp 6 trường hà nội amsterdam năm học 2023 2024. Các em theo dõi bài viết để lựa chọn cách làm mà mình thấy phù hợp nhất nhé. Chúc các em học tập tốt!
Hàng năm, kỳ thi khó nhất và đề thi hay và khó nhất dành cho học sinh lớp 5 lên lớp 6 tại Hà Nội, có lẽ là kỳ thi vào lớp 6 trường Hà Nội Amsterdam. Đề thi môn Toán cũng được mong đợi để xem mức độ như thế nào, các bài tự luận về chủ đề gì. Năm nay, đề thi có bài hình dưới đây, một bài toán “vừa vặn” với vai trò là bài tự luận về hình học trong đề thi, cũng giống như phong cách của các bài tự luận về hình học trong các đề năm trước, đủ khó và đủ ngắn gọn để phân loại được học sinh.
Hôm qua, ngay sau khi học sinh thi xong, học sinh nhớ lại đề và thầy Hiếu đã giải ngay bài toán đó cho nóng hổi để học sinh so sánh đáp số. Sau đó có suy nghĩ thêm thì tìm được khá nhiều lời giải khác, các lời giải đó được trình bày trong bài viết này.
Chú ý rằng: khi đi thi, một lời giải “ngắn” là lời giải mà học sinh mất ít thời gian để làm nó. Có thể hướng giải đó không phải là gọn gàng và hay, nhưng không lấy mất nhiều thời gian của học sinh, thì đó cũng là một lời giải hiệu quả.
Mỗi học sinh, khi học tập, ôn luyện có thể hiểu và nhớ một số bài toán “gốc”, một số tính chất quen thuộc, hay một vài phương pháp “mạnh”, khi vào phòng thi, học sinh khai thác theo hướng mà mình quen thuộc để tìm tòi lời giải bài toán. Lời giải hay khi đi thi là lời giải nhanh chóng, mất ít thời gian trong phòng thi.
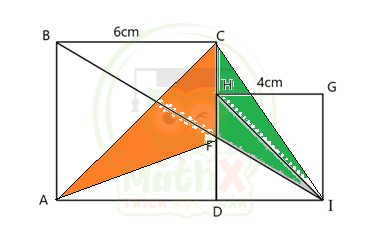
Bài toán. Cho hình vuông ABCD có cạnh 6cm và hình vuông DHGI có cạnh 4cm như hình vẽ dưới đây. Nối BI cắt CD ở F. Tính diện tích tam giác FHI?
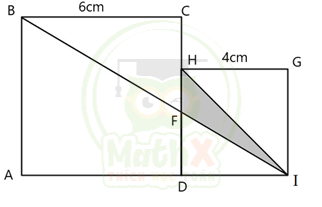
Đây là cách nghĩ ngay sau khi học sinh ra khỏi phòng thi và trao đổi đề với thầy Hiếu. Cách này dựa trên một phương pháp “mạnh” có thể áp dụng cho nhiều bài toán khác nhau, tuy nhiên có thể là một cách giải hơi dài hoặc chưa được gọn.
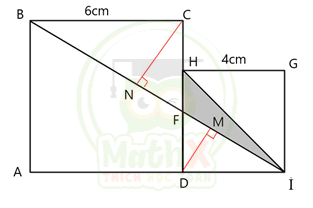
Ta phân tích thấy nếu tính được đoạn FH, ta sẽ tính ngay được diện tích tam giác FHI. Do đó ta đi tính FH, dựa vào việc xét tỉ số độ dài các đoạn thẳng dưới đây.
\(\dfrac{FD}{FC}=\dfrac{{{S}_{FDI}}}{{{S}_{FCI}}}\) (Chung chiều cao hạ từ I) (1)
\(\dfrac{{{S}_{FDI}}}{{{S}_{FCI}}} = \dfrac{DM}{CN}\) (Chung đáy FI) (2)
\(\dfrac{{{S}_{BDI}}}{{{S}_{BCI}}} = \dfrac{DM}{CN}\) (Chung đáy BI) (3)
Từ (1), (2), (3) \(\Rightarrow \dfrac{FD}{FC}=\dfrac{{{S}_{BDI}}}{{{S}_{BCI}}}=\dfrac{\dfrac{1}{2}\times BA\times DI}{\dfrac{1}{2}\times BC\times AB}=\dfrac{DI}{AB}=\dfrac{4}{6}=\dfrac{2}{3}\)
\(\Rightarrow FD=\dfrac{2}{2+3}\times CD=\dfrac{2}{5}\times 6=2,4(cm)\)
\(\Rightarrow FH=4-2,4=1,6(cm)\)
\({{S}_{FHI}}=\dfrac{1}{2}\times HF\times ID=\dfrac{1}{2}\times 1,6\times 4=3,2(c{{m}^{2}})\)
Nhận xét: Bài toán trên sử dụng phương pháp “lật mặt” để giải, ở đây đã có bước chuyển từ chung chiều cao (có tỉ số hai cạnh đáy) sang xét chung cạnh đáy (có tỉ số hai chiều cao). Phương pháp này hiệu quả trong việc giải rất nhiều bài toán về tỉ số diện tích của tiểu học.
Hình vẽ gợi cho ta việc nối BH, khi đó tam giác BHI rất “quen thuộc” trong các bài toán tính diện tích bằng phương pháp gián tiếp.
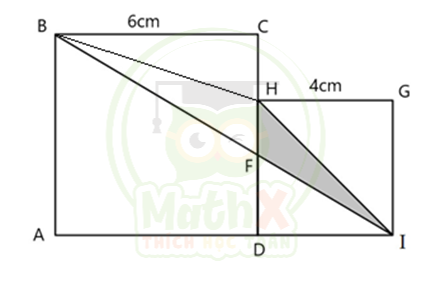
Ta có: \( {{S}_{BHI}}={{S}_{ABCD}}+{{S}_{DHGI}}-{{S}_{ABI}}-{{S}_{BCH}}-{{S}_{HGI}}\)
Thay số ta được:
\({{S}_{BHI}}=6\times 6+4\times 4-\dfrac{1}{2}\times 6\times (6+4)-\dfrac{1}{2}\times 6\times (6-4)-\dfrac{1}{2}\times 4\times 4=8(c{{m}^{2}})\)
Đến đây, để tính được diện tích tam giác FHI ta cần tìm tỉ số diện tích BHF và FHI. Một cách rất tự nhiên ta có:
\(\dfrac{{{S}_{BHF}}}{{{S}_{FHI}}}=\dfrac{BC}{DI}\) (hai tam giác có chung đáy HF) hay \(\dfrac{{{S}_{BHF}}}{{{S}_{FHI}}}=\dfrac{6}{4}=\dfrac{3}{2}\), từ đó suy ra \({{S}_{FHI}}=\dfrac{2}{2+3}\times {{S}_{BIH}}=\dfrac{2}{5}\times 8=3,2(c{{m}^{2}})\)
Cách này chỉ là xử lý khác đi của cách số 2, có thể một số học sinh thành thạo về tính chất hình thang sẽ nhìn ra và giải theo cách giải này.
Ta có: \({{S}_{BHI}}={{S}_{ABCD}}+{{S}_{DHGI}}-{{S}_{ABI}}-{{S}_{BCH}}-{{S}_{HGI}}\)
Thay số ta được:
\({{S}_{BHI}}=6\times 6+4\times 4-\dfrac{1}{2}\times 6\times (6+4)-\dfrac{1}{2}\times 6\times (6-4)-\dfrac{1}{2}\times 4\times 4=8(c{{m}^{2}})\)
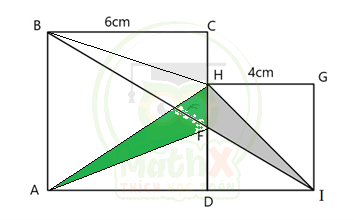
Vì ABHF là hình thang nên ta có \({{S}_{BHF}}={{S}_{AHF}}\) (hai tam giác chung đáy HF, chiều cao BC bằng chiều cao AD).
Ta có: \(\dfrac{{{S}_{AHF}}}{{{S}_{IHF}}}=\dfrac{\dfrac{1}{2}\times HF\times DI}{\dfrac{1}{2}\times HF\times AD}=\dfrac{DI}{AD}=\dfrac{4}{6}=\dfrac{2}{3} \\ => \dfrac{{{S}_{IHF}}}{{{S}_{AHF}}}=\dfrac{{{S}_{IHF}}}{{{S}_{BHF}}}=\dfrac{2}{3} \\ =>{{S}_{IHF}}=\dfrac{2}{2+3}\times 8=3,2(c{{m}^{2}})\)
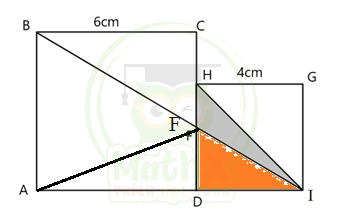
Cách tiếp cận của hướng giải này đó là thay vì tính diện tích FHI, ta sẽ đi tính diện tích FDI. Diện tích FDI, tất nhiên rồi, có thể tính được theo cách số 1, ta đi tính FD.
Ở cách giải này, ta sẽ tính diện tích FDI khi tính tỉ số của FDI so với diện tích của BDI.
Vì BFDA là hình thang nên ta suy ra \({{S}_{BFD}}={{S}_{AFD}}\) (chung đáy FD, chiều cao bằng nhau), đo đó ta có:
\(\dfrac{{{S}_{FDI}}}{{{S}_{BDI}}}=\dfrac{{{S}_{FDI}}}{{{S}_{BFD}}+{{S}_{FDI}}}=\dfrac{{{S}_{FDI}}}{{{S}_{AFD}}+{{S}_{FDI}}}=\dfrac{{{S}_{FDI}}}{{{S}_{AFI}}}=\dfrac{DI}{AI}=\dfrac{4}{4+6}=\dfrac{2}{5}\)
Từ đây suy ra: \({{S}_{FDI}}=\dfrac{2}{5}\times {{S}_{BDI}}=\dfrac{2}{5}\times \dfrac{1}{2}\times BA\times DI=\dfrac{2}{5}\times \dfrac{1}{2}\times 6\times 4=3,2(c{{m}^{2}})\)
Phụ huynh và các em học sinh xem thêm:
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS AMSTERDAM 2023-2024
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 2023
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 2020
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 2021
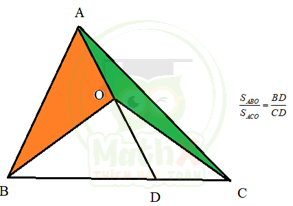
Cách tiếp cận để giải bài toán này, được dựa trên việc sử dụng tính chất vui “tàu bay giấy” thần thánh
Tính chất “tàu bay giấy” – Học sinh tự chứng minh tính chất này chỉ với 3 dòng. Chú ý đây chỉ là cách đặt tên cho vui, để học sinh dễ nhớ kiến thức. Thực tế học sinh cần chứng minh lại tính chất này trước khi sử dụng.
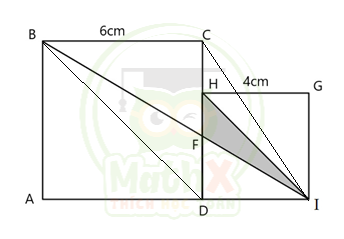
Nối CI, áp dụng tính chất trên ta có:
\(\dfrac{{{S}_{CHB}}}{{{S}_{CHI}}}=\dfrac{BF}{FI}=\dfrac{\dfrac{1}{2}\times BC\times CH}{\dfrac{1}{2}\times DI\times CH}=\dfrac{BC}{DI}=\dfrac{6}{4}=\dfrac{3}{2}\)
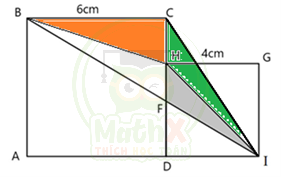
Mà: \(\dfrac{{{S}_{FDI}}}{{{S}_{BDI}}}=\dfrac{FI}{BI}\) nên ta có \({{S}_{FDI}}=\dfrac{2}{2+3}\times {{S}_{BDI}}=\dfrac{2}{5}\times \dfrac{1}{2}\times BA\times DI=\dfrac{1}{5}\times 6\times 4=4,8(c{{m}^{2}})\)
\(=> {{S}_{FHI}}={{S}_{DHI}}-{{S}_{FDI}}=\dfrac{1}{2}\times 4\times 4-4,8=3,2(c{{m}^{2}})\)
Cách này vẫn tiếp cận theo hướng đi tính tỉ số FI/BI như cách giải số 5. Ở đây sử dụng một cách rất hay đó là kéo được FI vào tam giác FIG, tam giác này lại rất dễ dàng để tính diện tích.
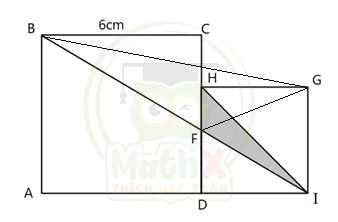
Ta có: \(\dfrac{FI}{BI}=\dfrac{{{S}_{FIG}}}{{{S}_{BIG}}}=\dfrac{\dfrac{1}{2}\times {{S}_{DHGI}}}{\dfrac{1}{2}\times GI\times (AD+DI)}=\dfrac{\dfrac{1}{2}\times 4\times 4}{\dfrac{1}{2}\times 4\times (6+4)}=\dfrac{2}{5}\)
Từ đó ta có thể giải tiếp theo cách 2 hoặc cách 5:
\({{S}_{FDI}}=\dfrac{2}{2+3}\times {{S}_{BDI}}=\dfrac{2}{5}\times \dfrac{1}{2}\times BA\times DI=\dfrac{1}{5}\times 6\times 4=4,8(c{{m}^{2}})\)
=> \({{S}_{FHI}}={{S}_{DHI}}-{{S}_{FDI}}=\dfrac{1}{2}\times 4\times 4-4,8=3,2(c{{m}^{2}})\)
hoặc: \({{S}_{BHI}}=6\times 6+4\times 4-\dfrac{1}{2}\times 6\times (6+4)-\dfrac{1}{2}\times 6\times (6-4)-\dfrac{1}{2}\times 4\times 4=8(c{{m}^{2}})\)
\({{S}_{FHI}}=\dfrac{2}{2+3}\times {{S}_{BIH}}=\dfrac{2}{5}\times 8=3,2(c{{m}^{2}})\)
Cách giải này tiếp cận theo hướng khai thác các yếu tố về hình thang. Vì đề bài cho hai hình vuông, nên ta có rất nhiều hình thang ở trong hình vẽ của bài toán này.
Nhắc lại tính chất của hình thang:
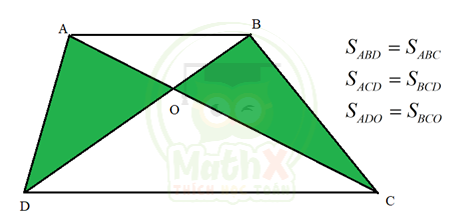
Nối F với A:
Ta có BCFA là hình thang, nên \({{S}_{BCF}}={{S}_{ACF}}\) (chung đáy CF, chiều cao là chiều cao của hình thang)
(thực ra mình nhìn dưới dạng hình thang thôi, còn thực tế ta lập luận theo công thức diện tích tam giác cũng suy ra được điều trên)
Ta có: \(\dfrac{FI}{FB}=\dfrac{{{S}_{CFI}}}{{{S}_{CFB}}}=\dfrac{{{S}_{CFI}}}{{{S}_{CFA}}}=\dfrac{DI}{DA}=\dfrac{2}{3}\)
Có tỉ số rồi, ta làm tiếp như các cách trên:
\({{S}_{FDI}}=\dfrac{2}{2+3}\times {{S}_{BDI}}=\dfrac{2}{5}\times \dfrac{1}{2}\times BA\times DI=\dfrac{1}{5}\times 6\times 4=4,8(c{{m}^{2}})\)
=> \({{S}_{FHI}}={{S}_{DHI}}-{{S}_{FDI}}=\dfrac{1}{2}\times 4\times 4-4,8=3,2(c{{m}^{2}})\)
Nhận xét: Thực chất cách số 7 không khác cách giải số 3 là mấy.
Cách giải này thực ra được “nhìn” từ một tính chất cũng rất đẹp về tỉ số diện tích trong hình tứ giác.
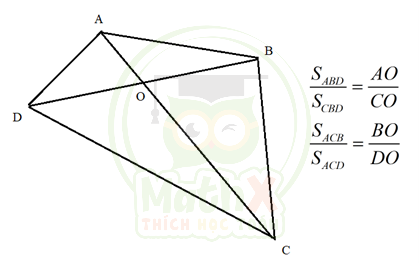
Học sinh hãy tự chứng minh tính chất trên, coi như một bài tập luyện tập.
Áp dụng tính chất trên cho tức giắc BDIC có hai đường chéo cắt nhau tại F, ta có:
\(\dfrac{{{S}_{BCD}}}{{{S}_{ICD}}}=\dfrac{BF}{IF}\) Suy ra: \(\dfrac{BF}{IF}=\dfrac{\dfrac{1}{2}\times 6\times 6}{\dfrac{1}{2}\times 6\times 4}=\dfrac{3}{2}\). Đến đây ta có tỉ số FI/FB và dễ dàng giải tiếp theo các bước ở các cách phía trên.
Phù, mệt rồi! Chắc chắn sẽ có thể giải theo các cách giải khác nữa.
Ta thấy các ý tưởng giải xoay quanh việc tính được tỉ số FI/FB hoặc tính được FH, FD… Cách 2, cách 3 và cách 6 khá hay!
Trên đây thầy Hiếu đã hướng dẫn các em 8 cách giải khác nhau cho bài toán hình học đề thi vào lớp 6 trường hà nội amsterdam năm học 2023 2024
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI LỚP 6 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX