
Trong các bài thi vào lớp 6 trường Hà Nội Amsterdam cũng như các trường THCS Chất lượng cao tại Hà Nội, phần hình học luôn là nội dung quan trọng, có nhiều bài khó và chiếm trọng số điểm cao. Để giúp các em học sinh có thêm tài liệu ôn tập, Thầy Hiếu và đội ngũ MATHX biên soạn và chia sẻ một số bài toán nâng cao, bài toán khó về nội dung hình học để các em tham khảo, phục vụ mục đích ôn thi vào cấp 2 chất lượng cao.
Các em học sinh xem thêm đề vào lớp 6 THPT Chuyên Hà Nội Amsterdam năm học 2023 - 2024 tại đây :
ĐÁP ÁN - ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS AMSTERDAM 2023-2024
Bài 1:
Cho 2 hình vuông ABCD và FGDE. so sánh \(S_{AFH}\) và \(S_{HDC}\) ?
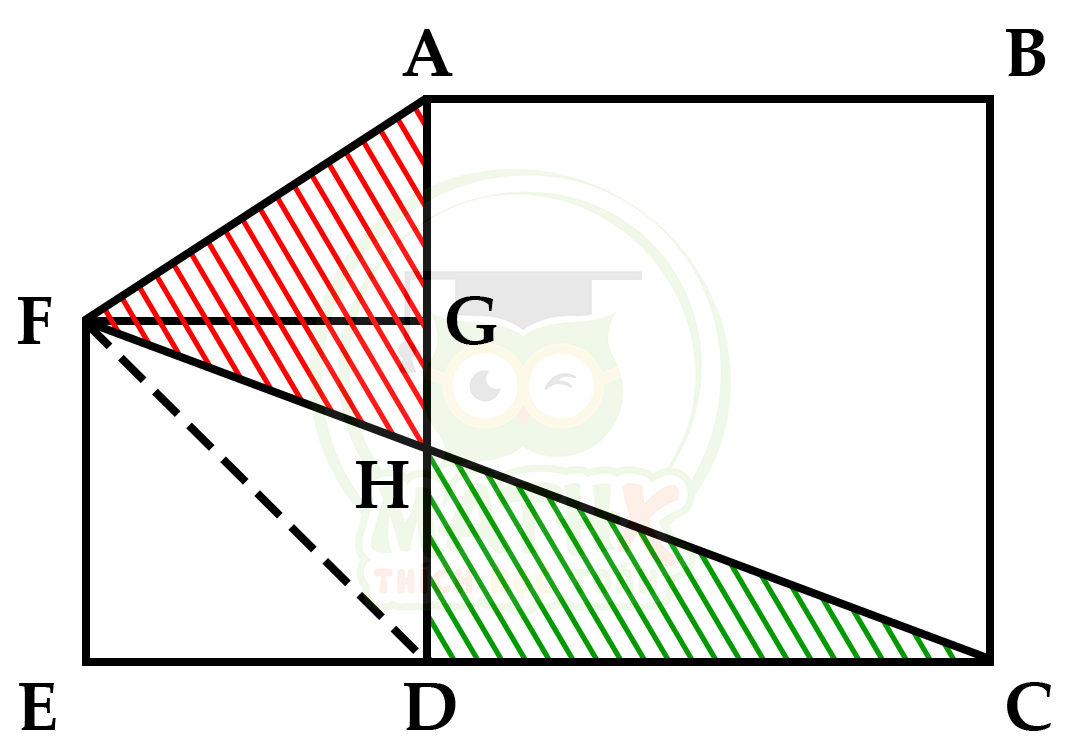
Giải
Ta thấy: \({{S}_{AFD}}={{S}_{FDC}}\) vì:
\({{S}_{AFD}}=\dfrac{FG \times AD}{2}\) ; \({{S}_{FCD}}=\dfrac{FE \times CD}{2}\)
Mà
EF = FG (cạnh hình vuông nhỏ)
AD = CD (cạnh hình vuông lớn)
=> \(\dfrac{FG \times AD}{2} =\dfrac{FE \times CD}{2}\)
Vậy: \({{S}_{AFD}}={{S}_{FDC}}\)
Ta lại có:
\({{S}_{AFD}}={{S}_{AFH}} + {{S}_{FHD}}\)
\({{S}_{FDC}}={{S}_{HDC}} + {{S}_{FHD}}\)
Mà
\({{S}_{AFD}}={{S}_{FDC}}\)
=> \({{S}_{AFH}} + {{S}_{FHD}} = {{S}_{HDC}} + {{S}_{FHD}}\)
=> \({{S}_{AFH}}={{S}_{HDC}}\) (đpcm)
Đáp số: \({{S}_{AFH}}={{S}_{HDC}}\)
Bài 2:
Cho hình bình hành ABCD. E là một điểm trên AB. Nối E với C và B với D. Gọi điểm giao nhau giữa EC và BD là F. Diện tích tam giác EFB là 20cm2 và BFC là 50cm2. Tính diện tích hình bình hành ABCD.
Giải
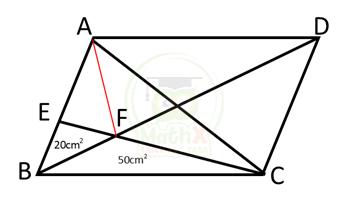
Ta có: SABD = SCBD, đáy BD chung => đường cao hạ từ đỉnh A bằng đường cao hạ từ đỉnh C xuống cạnh BD
SABF = SCBF = 50cm2 (vì có chung đáy AF, đường cao hạ từ đỉnh A bằng đường cao hạ từ đỉnh C xuống AF)
SAEF = SABF – SBEF = 50 – 20 = 30cm2
=>\(\dfrac{{A{\rm{E}}}}{{BE}} = \dfrac{{{S_{A{\rm{E}}F}}}}{{{S_{BEF}}}} = \dfrac{{30}}{{20}} = \dfrac{3}{2} \)
=> \(\dfrac{{{S_{CAE}}}}{{{S_{CBE}}}} = \dfrac{{A{\rm{E}}}}{{BE}} = \dfrac{3}{2} \Rightarrow {S_{CAE}} = \dfrac{3}{2} \times {S_{CBE}} = \dfrac{3}{2} \times \left( {20 + 50} \right) = 105(c{m^2})\)
\({S_{ABC{\rm{D}}}} = 2 \times {{\rm{S}}_{ABC}} = 2 \times \left( {{S_{CBE}} + {S_{CA{\rm{E}}}}} \right) = 2 \times \left( {70 + 105} \right) = 350\left( {c{m^2}} \right) \)
Đáp số: 350cm2
Đây là bài hình trong đề thi vào lớp 6 trường AMS năm học 2019 - 2020
Các em phụ huynh xem thêm các bài khác của để tại đây
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 2020
Bài 3
Hai hình vuông ABCD và FGDE. tính \({{S}_{AFC}}\) biết AB = 10cm
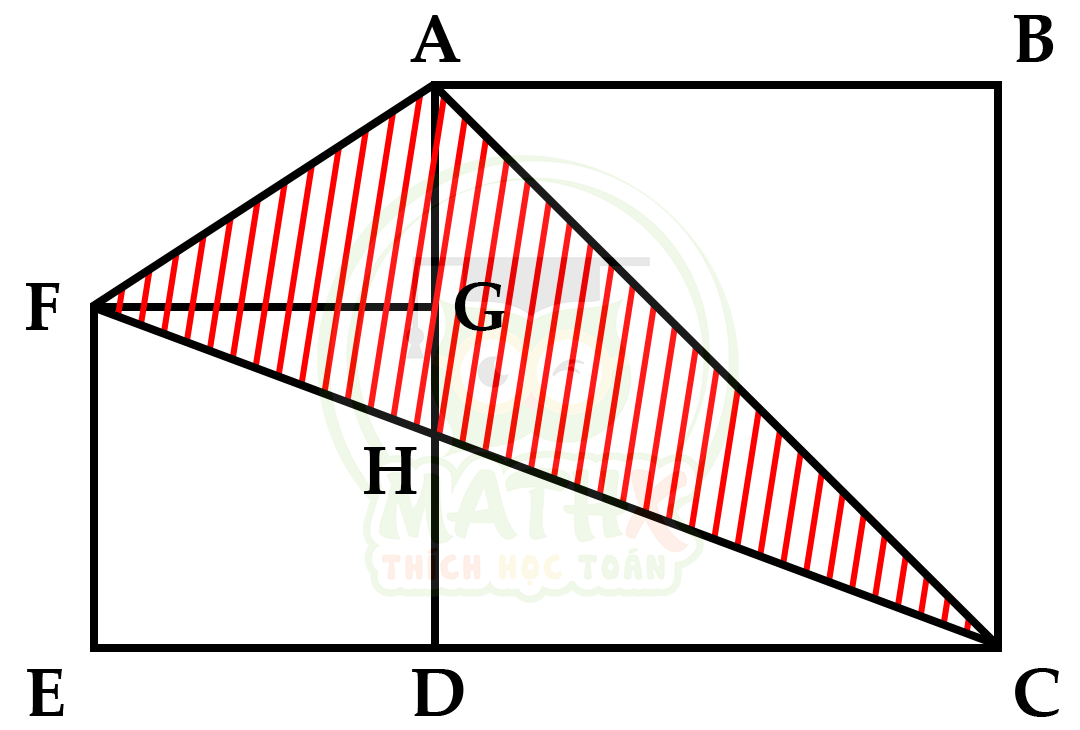
Giải
\({{S}_{AFD}}=\dfrac{FG \times AD}{2}\) ; \({{S}_{FCD}}=\dfrac{FE \times CD}{2}\)
EF = FG ; AD = CD (cạnh hình vuông)
=> \({{S}_{AFD}}={{S}_{FCD}}\)
=> \({{S}_{AFH}} + {{S}_{FHD}} = {{S}_{HDC}} + {{S}_{FHD}}\)
\({{S}_{AFH}}={{S}_{HDC}}\)
Ta có
\({{S}_{AFC}}={{S}_{AFH}} + {{S}_{AHC}}\)
=> \({{S}_{HDC}} + {{S}_{AHC}} = {{S}_{ADC}}\)
=> \({{S}_{AFC}} = \dfrac{1}{2} \times {{S}_{ABCD}} = \dfrac{1}{2} \times 10 \times 10 = 50 (cm^2)\)
Đáp số: \(50 cm^2\)
Bài 4:
Cho hình chữ nhật ABCD (như hình vẽ). M là một điểm trên cạnh CD. Nối AM và BD cắt nhau tại I. Biết diện tích \({S_{BMC}} = 36c{m^2} \) và \({S_{BMC}} = \dfrac{9}{{16}}{S_{IMD}}\) .Tính diện tích tam giác ABI.
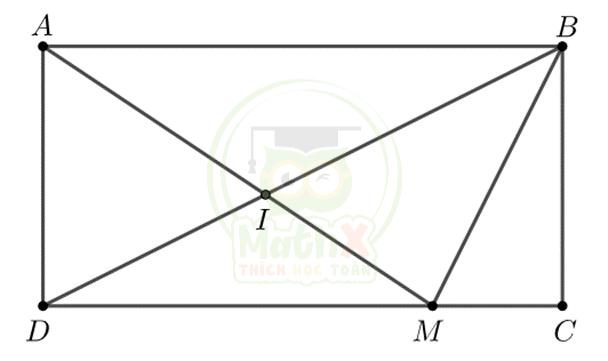
Giải
Diện tích tam giác MID là: 36 : 9 x 16 = 64 (cm2)
Tam giác ADM và tam giác BDM có chung đáy DM và có chiều cao bằng chiều chiều rộng của HCN ABCD nên \({S_{ADM}} = {S_{BDM}} \) .
=> \({S_{ADI}} + {S_{DIM}} = {S_{DIM}} + {S_{IBM}}\) => \({S_{ADI}} = {S_{IBM}} \)
Ta có: \({S_{ADB}} = {S_{BDC}} \)
Khi đó: \({S_{ABD}} - {S_{AID}} = {S_{BCD}} - {S_{BIM}} \) => \({S_{AIB}} = {S_{BMC}} + {S_{MID}} = 36 + 64 = 100\left( {c{m^2}} \right) \)
Đáp số: 100cm2
Đây là bài hình trong đề thi vào lớp 6 trường AMS năm học 2020 - 2021
Các em phụ huynh xem thêm các bài khác của để tại đây
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 2021
Bài 5:
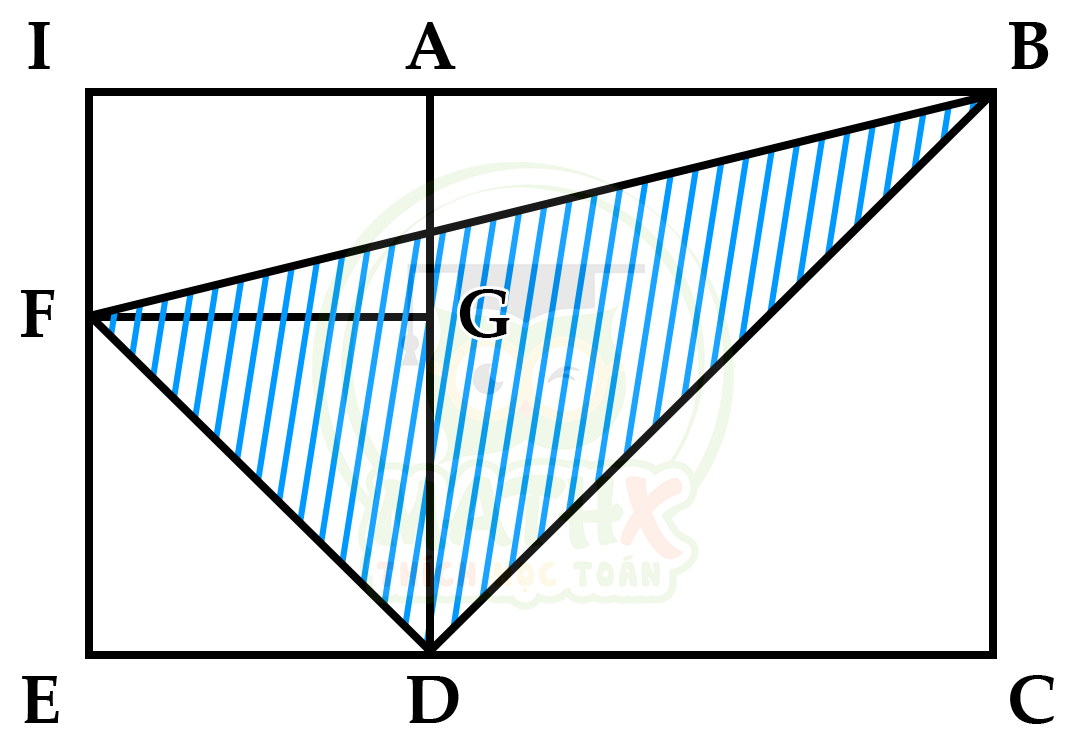
Cho 2 hình vuông ABCD và FGDE. Biết AB = 12cm; FG = 8cm. Tính \({{S}_{BFD}}\)
Giải
Kéo dài đường thẳng FE và AB cắt nhau tại I
=> IBCE là hình chữ nhật
Chiều dài hình chữ nhật IBCE là:
IB = IA + AB = 12 + 8 = 20 (cm) (vì IA = FG = 8cm)
Mà BC = AB (vì ABCD là hình vuông)
=> BC = AB = 12cm
=> \({{S}_{IBCE}} = IB \times BC = 20 \times 12 = 240 (cm^2)\)
\({{S}_{BCD}} = \dfrac {1}{2} \times {{S}_{ABCD}} = \dfrac {1}{2} \times 12 \times 12 = 72 (cm^2)\)
\({{S}_{EFD}} = \dfrac {1}{2} \times 8 \times 8 = 32 (cm^2)\)
\({{S}_{BIF}} = \dfrac {1}{2} \times FI \times IB \) (FI = IF - FE = 12 - 8 = 4cm)
=> \({{S}_{BIF}} = \dfrac {1}{2} \times 4 \times 20 = 40 (cm^2)\)
\({{S}_{BFD}} = {{S}_{IBCE}} - {{S}_{BCD}} - {{S}_{EFD}} - {{S}_{BIF}} \\ = 240 - 72 - 32 - 40 \\ = 96 (cm^2)\)
Đáp số: \(96 cm^2\)
Bài 6:
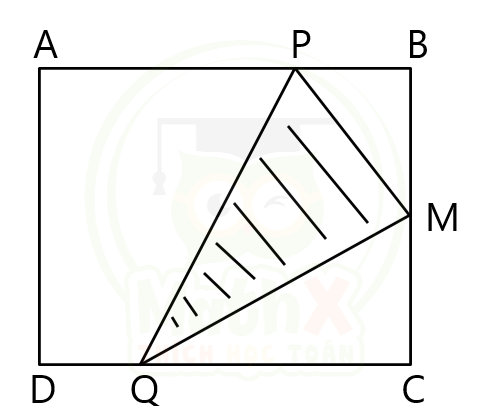
Cho hình chữ nhật ABCD. Trên cạnh AB lấy điểm P, trên cạnh CD lấy điểm Q sao cho AP = CQ. M là trung điểm BC. Biết AB = 16cm, BC = 12cm. Tính diện tích phần gạch chéo?
Giải
Vì AP bằng CQ và AB = CD nên BP = DQ
\(\Rightarrow {{S}_{APQD}}=\text{ }{{S}_{PBCQ}}=\dfrac{1}{2}{{S}_{ABCD}}=\dfrac{1}{2}\times 16\times 12=96\left( c{{m}^{2}} \right)\)
Ta có:
\({{S}_{PBM}}=\dfrac{1}{2}\times PB\times BM\)
\({{S}_{QCM}}=\dfrac{1}{2}\times QC\times MC=\dfrac{1}{2}\times QC\times BM\) (vì MC = BM)
-> \(\begin{align} & {{S}_{PBM}}+{{S}_{QCM}}=\dfrac{1}{2}\times PB\times BM+\dfrac{1}{2}\times QC\times BM \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}\times BM\times \left( PB+QC \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}\times \dfrac{1}{2}\times BC\times \left( PB+QC \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}{{S}_{PBCQ}}=48\left( c{{m}^{2}} \right) \\ \end{align}\)
Vậy diện tích phần gạch chéo là: 96 – 48 = 48 (cm2)
Đáp số: 48cm2.
Đây là bài hình trong đề thi vào lớp 6 trường AMS năm học 2022 - 2023
Các em phụ huynh xem thêm các bài khác của để tại đây
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 2023
Bài 7:
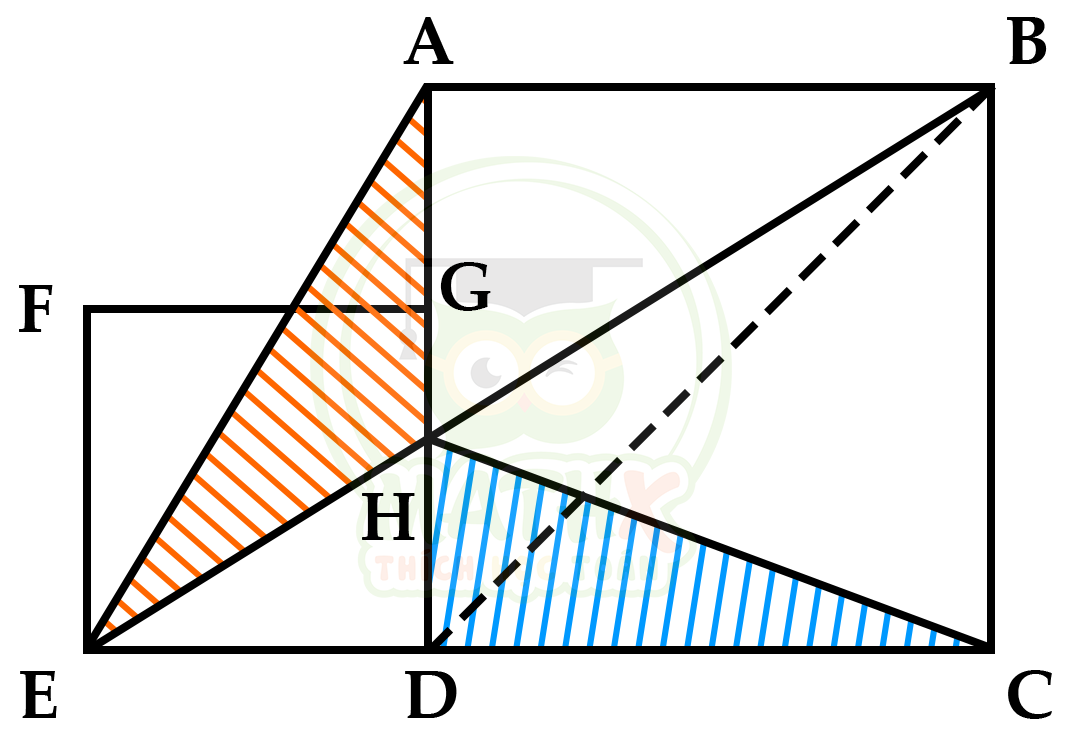
Hai hình vuông ABCD và FGDE. So sánh: \({{S}_{AHE}}\) và \({{S}_{HDC}}\)
Giải
Cách 1:
\({{S}_{DBC}} = {{S}_{HBC}}\) (2 tam giác có đường cao bằng nhau là cạnh hình vuông và có đáy chung BC)
Mà
\({{S}_{BDC}} = \dfrac {1}{2} \times {{S}_{ABCD}}\)
=> \({{S}_{HBC}} = \dfrac {1}{2} \times {{S}_{ABCD}}\)
Mà
\({{S}_{AHB}} + {{S}_{HDC}} = {{S}_{ABCD}} - {{S}_{HBC}} = {{S}_{ABCD}} - \dfrac {1}{2} \times {{S}_{ABCD}}\)
=> \({{S}_{AHB}} + {{S}_{HDC}} = \dfrac {1}{2} \times {{S}_{ABCD}}\)
\({{S}_{EAB}} = CB \times AB \times \dfrac {1}{2} = \dfrac {1}{2} \times {{S}_{ABCD}}\)
\({{S}_{EAB}} = {{S}_{AHE}} + {{S}_{AHB}} = \dfrac {1}{2} \times {{S}_{ABCD}}\)
=> \({{S}_{AHB}} + {{S}_{HDC}} = {{S}_{AHE}} + {{S}_{AHB}}\)
=> \({{S}_{AHE}} = {{S}_{HDC}} \)
Cách 2:
Ta có:
\({{S}_{AHE}}= {{S}_{BHD}} \) (1)
Vì
\({{S}_{ABE}} = {{S}_{AHE}} + {{S}_{AHB}}\)
\({{S}_{ABD}} = {{S}_{ABH}} + {{S}_{BHD}}\)
\({{S}_{ABE}} = {{S}_{ABD}}\) (có đường cao hạ xuống đáy BC bằng nhau)
\({{S}_{BHD}} = {{S}_{HDC}} \) (2 tam giác có đường cao hạ xuống đáy HD bằng nhau) (2)
Từ (1) và (2) => \({{S}_{AHE}} = {{S}_{HDC}}\)
Đáp số: \({{S}_{AHE}} = {{S}_{HDC}}\)
Bài 8:
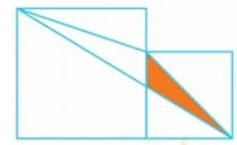
Cho hình vẽ. Biết hình vuông nhỏ có cạnh 4cm, hình vuông lớn có cạnh 6cm. Tính diện tích phần tô đậm.
Giải
Gọi tên các điểm như hình vẽ
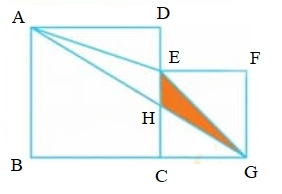
Tổng diện tích hai hình vuông là: 6 x 6 + 4 x 4 = 52 (cm2)
Diện tích tam giác ADE là: 6 x (6 - 4) : 2 = 6 (cm)
Diện tích tam giác EFG là: 4 × 4 : 2 = 8 (cm)
Diện tích tam giác ABG là: 6 x (6 + 4) : 2 = 30 (cm)
Diện tích tam giác AEG là: 52 – 6 – 8 – 30 = 8 (cm)
Xét tam giác AEH và tam giác GEH có chung đáy EH nên \(\dfrac{{{S_{AEH}}}}{{{S_{GEH}}}} = \dfrac{{AD}}{{GC}} = \dfrac{6}{4} = \dfrac{3}{2}\)
Suy ra diện tích tam giác GEH là
8 : (3 + 2) x 2 = 3,2 (cm2)
Đáp số: \(3,2 cm^2\)
Đây là bài hình trong đề thi vào lớp 6 trường AMS năm học 2022 - 2023
Các em phụ huynh xem thêm các bài khác của để tại đây
HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 2024
Bài 9:
Cho 2 hình vuông ABCD và FGDE, EG cắt AB tại H. So sánh AH và AG
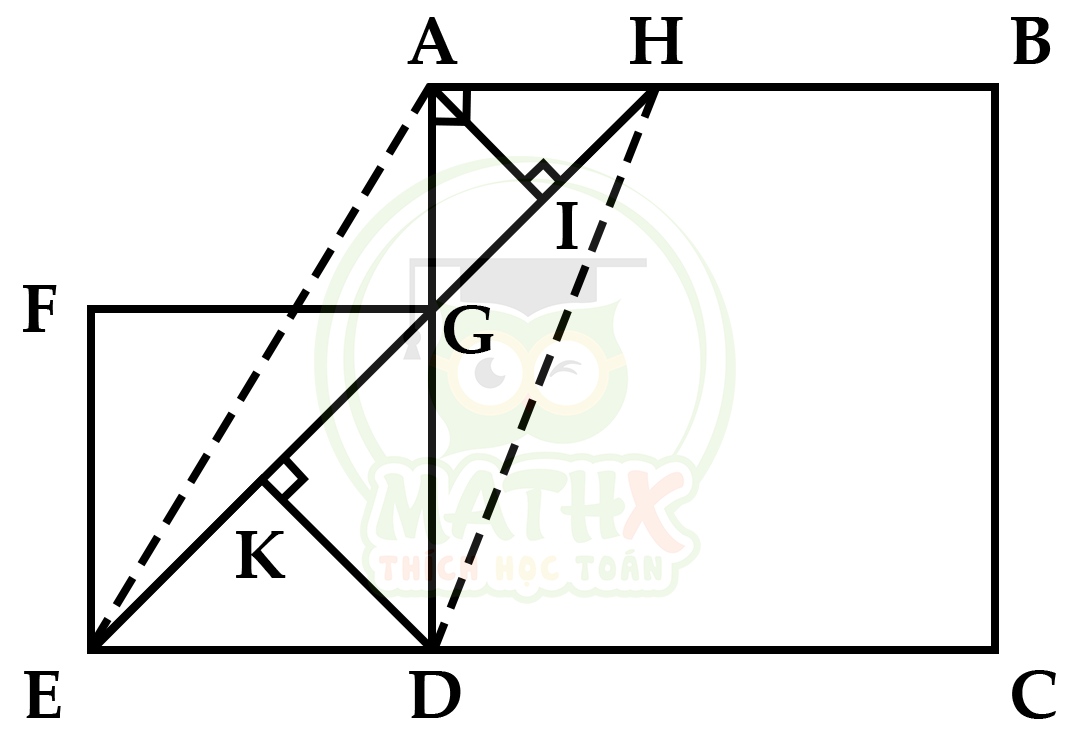
Giải
Nối A và E; H và D, ta có được hình thang AHDE
Ta có:
\(\dfrac {AH}{ED} = \dfrac {{{S}_{AEH}}}{{{S}_{DEH}}}\) (2 tam giác có đường cao từ A và D xuống đáy chung EH)
\(\dfrac {{{S}_{AEH}}}{{{S}_{DEH}}} = \dfrac {AI}{DK}\) (2 tam giác có đáy chung EH)
\(\dfrac {AI}{DK} = \dfrac { S_{AGH} } { S_{DGH} }\) (2 tam giác có đáy chung GH)
\(\dfrac {{{S}_{AGH}}}{{{S}_{DGH}}} = \dfrac {AG}{GD}\) (2 tam giác có chung đường cao AH xuống đáy AD)
=> \(\dfrac {AH}{ED} = \dfrac {AG}{GD}\)
Mà ED = GD (cạnh hình vuông nhỏ)
=> AH = AG
Đáp số: AH = AG
Bài 10:
Cho hình thang ABCD, lấy điểm M trên AC sao cho AM = 2 x MC. Lấy điểm N trên CD sao cho BDNM là hình thang.
a) So sánh \({{S}_{BDM}}\) với \({{S}_{BND}}\)
b) Tính tỉ số \(\dfrac{{{S}_{ABND}}}{{{S}_{BNC}}}\)
Giải:
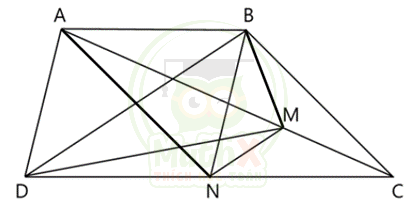
a) Có BDNM là hình thang nên ta có \({{S}_{BDM}}\) = \({{S}_{BDN}}\)
Vì chung đáy BD và chiều cao từ M xuống đáy = chiều cao từ N xuống đáy = chiều cao của hình thang BDNM.
b) Ta có
\({{S}_{BDM}}={{S}_{BDN}}\) nên \({{S}_{ABMD}}={{S}_{ABND}}\)
Mà: \({{S}_{ABM}}=2\times {{S}_{BMC}}\) , \({{S}_{ADM}}=2\times {{S}_{DMC}}\) nên
\({{S}_{ABMD}}=2\times \left( {{S}_{BMC}}+{{S}_{DMC}} \right)=2\times \left( {{S}_{BMC}}+{{S}_{MNC}}+{{S}_{DMN}} \right)\)
\({{S}_{ABMD}}=2\times \left( {{S}_{BMC}}+{{S}_{MNC}}+{{S}_{BMN}} \right)\) (do \({{S}_{NDM}}={{S}_{BMN}}\) )
\({{S}_{ABMD}}=2\times {{S}_{BNC}}\)
\(\Rightarrow \frac{{{S}_{ABND}}}{{{S}_{BNC}}}=\dfrac{2}{1}\)
Đáp số:
a. \({{S}_{BDM}}\) = \({{S}_{BDN}}\)
b. \(\frac{{{S}_{ABND}}}{{{S}_{BNC}}}=\dfrac{2}{1}\)
Qua các bài toán trên, thầy Hiếu hi vọng rằng các em học sinh sẽ học hỏi được một số kiến thức khó về hình học, về phương pháp tỉ số diện tích trong các bài toán hình học lớp 5, qua đó vững vàng kiến thức để có thể ôn thi tốt vào các trường cấp 2 Chất Lượng Cao (CLC) tại Hà Nội.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX