
Đội ngũ MATHX biên soạn gửi đến phụ huynh và các em học sinh giải chi tiết đề thi học bổng THCS Ngôi Sao Hà Nội vòng 2 năm học 2023-2024. Hy vọng rằng tài liệu này sẽ hỗ trợ quá trình ôn tập và nâng cao khả năng giải bài tập của các em. Chúc các em học tốt!
Để biết thêm thông tin về trường và phương thức tuyển sinh vào 6 THCS Ngôi Sao mới nhất PHHS tham khảo tại đây:
GIỚI THIỆU VỀ TRƯỜNG THCS NGÔI SAO
THÔNG TIN TUYỂN SINH VÀO LỚP 6 TRƯỜNG NGÔI SAO HÀ NỘI NĂM HỌC 2024-2025
Ngoài ra PHHS tham khảo thêm một số tài liệu phục vụ cho ôn thi vào 6 THCS Ngôi Sao tại đây:
GIẢI CHI TIẾT ĐỀ TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS NGÔI SAO 2020 2021
GIẢI CHI TIẾT ĐỀ TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS NGÔI SAO 2021 2022
GIẢI CHI TIẾT ĐỀ TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS NGÔI SAO 2023 2024
TÀI LIỆU THAM KHẢO KHỐI 5 ÔN THI HỌC BỔNG THCS NGÔI SAO 2023
Các em nhấn vào link phía bên dưới tải đề về làm trước khi xem lời giải và đáp án:
Bài 1: Cho 2025 ⃞ 2024 ⃞ 2023 ⃞ … ⃞ 2 ⃞ 1
Những ô vuông có thể điền dấu "+" hoặc dấu "-”.
a) Kết quả có thể là số chẵn được không? Vì sao?
b) Điền vào những ô trống để được kết quả nhỏ nhất.
Hướng dẫn:
a) Giả sử nếu tất cả các ô vuông đều là dấu “+”
=> Phép tính trên sẽ có kết quả là:
2025 + 2024 + …. + 2 + 1 = (2025 + 1) x 2025 : 2 = 2051325
Nếu thay bất kể dấu “+” nào ở trước ô có giá trị bằng a thành dấu “-” thì kết quả của phép tính sẽ giảm đi 2 x a đơn vị
Mà kết quả 2051325 là số lẻ nên khi ta giảm đi 2 x a đơn vị thì vẫn thu được kết quả là số lẻ
=> Kết quả không thể là số chẵn
b) Vì kết quả không thể là số chẵn nên giá trị nhỏ nhất mà phép tính trên có thể có được là = 1 (nếu kết quả có thể là số chẵn gì phép tính trên sẽ có giá trị nhỏ nhất = 0)
Để có thể tính ra kết quả = 1, ta sẽ bỏ số 1 cuối cùng ra ngoài. Khi đó phép tính trên sẽ có tổng 2024 số, ta sẽ chia 4 số thành 1 nhóm, mỗi nhóm này sẽ có tổng và hiệu = 0
=> Phép tính trên sẽ được viết lại như sau (phép tính khi đã loại bỏ số 1 ra ngoài để có được kết quả = 1)
2025 – 2024 – 2023 + 2022 + 2021 – 2020 – 2019 + 2018 + … + 5 – 4 – 3 + 2 = 0
Bài 2: Cho các số theo thứ tự sau: 2023, a, b, c, d, e, f. Kể từ số b thì số này sẽ bằng trung bình cộng của hai số liền trước nó và khoảng cách giữa hai số e và f là 2 đơn vị. Hỏi giá trị nhỏ nhất của a là bao nhiêu?
Hướng dẫn:
Vì khoảng cách giữa 2 số e và f là 2 đơn vị và số f bằng trung bình cộng của hai số d và e nên khoảng cách giữa hai số d và e là 2 x 2 = 4 đơn vị
Lập luận tương tụ, ta suy ra được khoảng cách giữa hai số c và d là 4 x 2 = 8 đơn vị; khoảng cách giữa hai số b và c là 8 x 2 = 16 đơn vị; khoảng cách giữa 2 số a và b là 16 x 2 = 32 đơn vị
Ta sẽ có sơ đồ như sau:
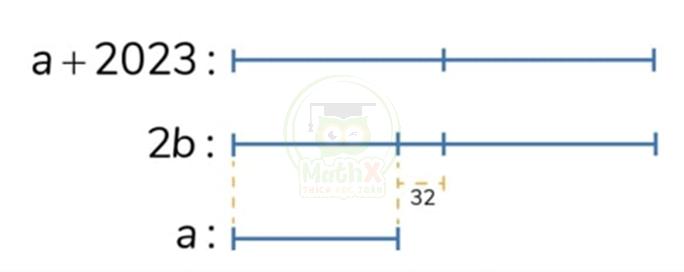
Từ sơ đồ trên, ta thấy 2 lần số a kém a + 2023 là 64 đơn vị
Vậy số a = 2023 – 32 x 2 = 1959.
Đáp số: 1959.
Bài 3: Cho tam giác ABC có D là trung điểm AB và E là trung điểm AC. Gọi O là một điểm nằm bên trong tam giác ABC. Nối D với O, B vớii O, C với O và E với O. Nối D với E. Biết diện tích tam giác ABC la 42 cm và diện tích tứ giác ADOE là 15 cm.
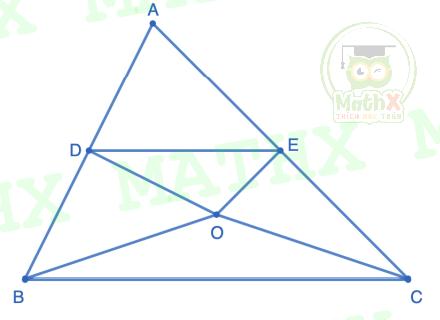
a) Tính diện tích tam giác DOE
b) Tính diện tích tam giác BOC.
Hướng dẫn:
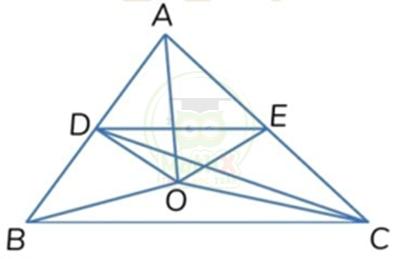
Nối C với D và A với O
a)
Xét \(\Delta ABC \) và \(\Delta ADC\) có chung chiều cao hạ từ C xuống AB nên
\(\dfrac {S_{ADC}}{S_{ABC}} = \dfrac {AD}{AB} = \dfrac {1}{2}\) (do D là trung điểm của AB)
\(\Rightarrow S_(ADC) = \dfrac {1}{2} \times S_(ABC) = \dfrac {1}{2} \times 42 = 21 (cm^2)\)
Xét \( \Delta ADE\) và \(\Delta ADC\) có chung chiều cao hạ từ D xuống AC nên
\(\dfrac {S_{ADE}}{S_{ADC}} = \dfrac {AE}{AC} = \dfrac {1}{2} \) (do E là trung điểm của AC)
\(\Rightarrow S_{ADE} = \dfrac {1}{2} \times S_{ADC} = \dfrac {1}{2} \times 21 = 10,5 (cm^2)\)
Vậy \(S_{DOE} = S_{ADOE} \ – S_{ADE} = 15 \ – 10,5 = 4,5 (cm^2)\)
b)
Xét \(\Delta OAB\) và \(\Delta OAD\) có chung chiều cao hạ từ O xuống AB nên
\(\dfrac {S_{OAB}}{S_{OAD}} = \dfrac {AB}{AD} = 2 \) (do D là trung điểm của AB)
\(\Rightarrow S_{OAB} = 2 \times S_{OAD}\)
Xét \(\Delta OAC\) và \(\Delta OAE\) có chung chiều cao hạ từ O xuống AC nên
\(\dfrac {S_{OAC}}{S_{OAE}} = \dfrac {AC}{AE} = 2 \) (do E là trung điểm của AC)
\(\Rightarrow S_{OAC} = 2 \times S_{OAE}\)
Từ đó, ta có:
\(S_{OAB} + S_(OAC) = 2 \times S_{OAD} + 2 \times S_{OAE} = 2 \times (S_{OAD} + S_{OAE}) = 2 \times S_{ADOE} = 2 \times 15 = 30 (cm^2)\)
Vậy \(S_{OBC} = S_{ABC} – (S_{OAB} + S_{OAC}) = 42 \ – 30 = 12 (cm^2)\)
Đáp số: a: 4,5 \(cm^2\): b: 12 \(cm^2\)
Bài 4: Cho hinh vẽ sau: Hỏi nếu nối tất cả các điểm với nhau thì sẽ được tất cả bao nhiêu tam giác?
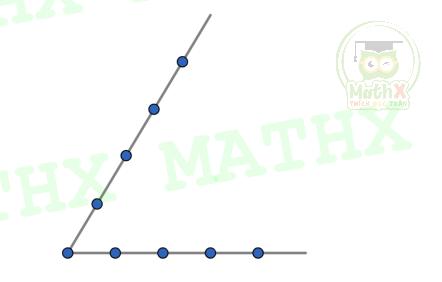
Hướng dẫn:
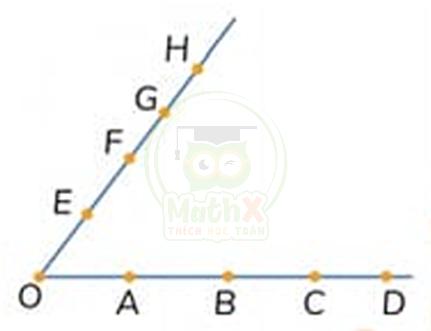
Ta gọi các điểm như hình vẽ phía trên
Để tạo thành 1 tam giác, ta lựa chọn 1 đoạn thẳng bất kì và 1 điểm không nằm trên đường thẳng đó
Ví dụ:
Đoạn thẳng OA, ta lựa chọn các đỉnh E, F, G, H để tạo thành 1 tam giác
Xét 5 điểm O, A, B, C, D, số đoạn thẳng tạo thành là:
5 x 4 : 2 = 10 (đoạn thẳng)
Mỗi đoạn thẳng này có thể tạo với 1 trong 4 điểm E, F, G, H để tạo thành 1 tam giác
Do đó số tam giác tạo thành là:
10 x 4 = 40 (tam giác)
Xét 5 điểm O, E, F, G, H, số đoạn thẳng tạo thành là:
5 x 4 : 2 = 10 (đoạn thẳng)
Tuy nhiên, nếu chọn các đoạn thẳng OE, OF, OG, OH làm 1 cạnh của tam giác thì khi chọn 1 trong 4 điểm ABCD làm đỉnh còn lại của tam giác sẽ cho các tam giác trùng với tam giác ở phía bên trên. Ví như như \Delta FOB sẽ trùng với \Delta BOF
Do đó số tam giác tạo thành từ trường hợp này sẽ chỉ là:
(10 - 4) x 4 = 24 (tam giác)
Vậy số tam giác tạo thành khi nối tất cả các điểm trên là:
40 + 24 = 64 (tam giác)
Đáp số: 64 tam giác
Bài 5: Bốn bạn Việt, Nam, Chiến, Thắng chơi ném bóng tính điểm và có kết quả như sau:
- Nam có tổng điểm cao hơn tổng điểm của Việt và Chiến.
- Tổng điểm của Nam và Việt bằng tổng điểm của Thắng và Chiến.
- Tổng điểm của Thắng và Việt lớn hơn tổng điểm của Nam và Chiến.
Xác định thứ hạng của mỗi người.
Hướng dẫn:
Vì Nam có điểm cao hơn tổng điểm của Việt và Chiến nên điểm của Nam sẽ cao hơn điểm của bạn Việt và điểm của bạn Chiến
=> Nam > Việt, Nam > Chiến
Vì tổng điểm của Nam và Việt bằng tổng điểm của Thắng và Chiến nên mỗi cặp Nam, Việt và Thắng, Chiến sẽ có tổng điểm bằng 1 nửa tổng điểm của cả 4 bạn
Nam + Việt = Thắng + Chiến
=> Nam + Việt = Thắng + Chiến = (Nam + Việt + Thắng + Chiến) : 2
Tổng điểm của Thắng và Việt lớn hơn tổng điểm của Nam và Chiến nên tổng điểm của Thắng và Việt sẽ lớn hơn 1 nửa tổng điểm của cả 4 bạn
Thắng + Việt > Nam + Chiến
=> Thắng + Việt > (Nam + Việt + Thắng + Chiến) : 2
=> Thắng + Việt > Nam + Việt
=> Thắng > Nam
=> Điểm của Thắng lớn hơn điểm của Nam
Tổng điểm của Nam và Việt bằng tổng điểm của Thắng và Chiến mà ta đã có điểm của Thắng lớn hơn điểm của Nam nên điểm của Việt lớn hơn điểm của Chiến
Nam + Việt = Thắng + Chiến
Thắng > Nam
=> Việt > Chiến
=> ta có thứ tự như sau:
Thắng > Nam > Việt > Chiến
Vậy Thắng có số điểm cao nhất, Nam có số điểm cao thứ 2, Việt có số điểm cao thứ 3 và Chiến có số điểm thấp nhất
Trên đây MATHX đã hướng dẫn các em giải chi tiết đề thi học bổng ngôi sao Hà Nội vòng 2 năm học 2023 - 2024. Chúc các em học và ôn tập thật tốt thành công trong kì thi sắp tới.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS NGÔI SAO được đội ngũ MATHX biên soạn, đầy đủ và chi tiết nhất để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Thầy Hiếu hướng dẫn các em học sinh giải đề thi tham khảo của kỳ thi Học bổng Ngôi Sao Hà Nội - đề số 1, 2 và 3: